
Учебное пособие 1959
.pdfаппроксимировать решением стационарного уравнения диффузии, отвечающего граничным условиям:
c c0 при r re; c c при r (t),
где c0 - исходная концентрация в матрице, а c -
концентрация в матрице, находящейся в равновесии с зародышем. Это стационарное решение справедливо для выделения, т.е. только при r .
Поскольку задача имеет сферическую симметрию, то второе уравнение Фика для стационарной задачи удобно записать в сферических координатах:
|
2c |
|
|
|
2 c |
|
||||
|
|
|
|
|
|
|
|
0. |
||
|
r2 |
|
|
|
||||||
|
|
|
|
r r |
|
|||||
Его решение запишется как: |
|
|
|
|
|
|||||
|
c |
b |
d , |
|
||||||
|
|
|
||||||||
|
|
|
|
|
r |
|
|
|
|
|
где b и d - константы |
|
|
интегрирования. Используя |
|||||||
граничные условия и полагая re (t), получим: |
||||||||||
c(r) |
(c |
|
c ) |
c . |
||||||
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
r |
0 |
|
|
|
|
|
|
|
|
|
|
||
Теперь искомый поток J( ) можно определить из первого уравнения Фика, записанного в сферических координатах:
|
c |
|
(c |
|
||
|
c ) |
|||||
J( ) D |
|
|
D |
0 |
|
. |
|
|
|
||||
r r (t) |
|
(t) |
||||
Подставляя его значение в уравнение (1.46) можно записать следующее кинетическое уравнение:
31
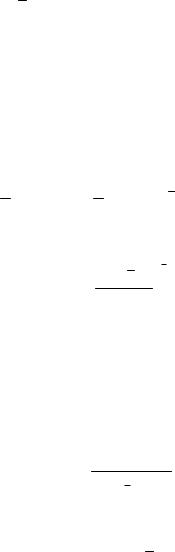
|
c |
|
3D |
(c0 c ) (t). |
(1.47) |
t |
r3 |
||||
|
|
|
e |
|
|
Здесь присутствует «неудобный» параметр (t). Для его определения выведем ещё одно кинетическое уравнение из баланса, растворенного вещества. Обозначим через cp -
концентрацию растворенного вещества внутри зародыша и предположим, что при t 0 зародыш отсутствует, т.е. 0. Тогда
4 cp 3(t) 4 re3 c0 c(t) . 3 3
Решая это уравнение относительно (t), получим
1
(t) re c0 c(t) 3 .cp
Подставляя этот результат в уравнение (1.47), получим следующее кинетическое уравнение:
|
|
|
|
3D(c0 |
c ) |
|
|
|
1 |
|
|
|||
c |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
t |
|
|
|
1 |
|
|
(c0 |
c(t)) |
|
. |
(1.48) |
|||
|
|
c3r2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
p |
e |
|
|
|
|
|
|
||
Или, обозначив через b 3D(c10 c ) , получим вместо
cp3re2
уравнения (1.48) достаточно простое кинетическое уравнение
|
|
|
1 |
|
||||
|
c |
|
||||||
. |
|
b(c0 |
c |
) |
3 |
(1.49) |
||
t |
|
|||||||
|
|
|
|
|
|
|
||
После интегрирования имеем
32

|
3 |
2 |
|
||||
|
(c |
c |
) |
3 |
bt , |
||
|
|||||||
2 |
0 |
|
|
|
|
||
где - константа интегрирования, которая легко находится из начальных условий: при t 0;c0 c , так что
0. Поэтому
|
|
|
2bt |
3 |
|
|
|
|
|
2 |
|
|
|||
c c |
|
|
|
. |
(1.50) |
||
|
|||||||
0 |
|
3 |
|
|
|
||
Следует заметить, что это решения справедливо для малых времён, когда размер зародыша мал по сравнению с
эквивалентной сферой, т.е. |
re Dt . |
Если (0) 0, |
то |
|
уравнение (1.50) является |
хорошим |
приближением |
при |
|
c |
c0 2 3. |
|
|
|
Рассмотрим некоторые свойства полученного решения. Для сферического зародыша разность c0 c пропорциональна
t3/2 . Это следует из того, что радиус участка, из которого зародыш выкачал растворённое вещество, пропорционален t3/2 . Уравнение (1.50) просто констатирует, что концентрация c равна c0 минус член, пропорциональный количеству
вещества, выделившемуся из раствора.
Если бы частицы выделений были бы очень длинными прутками фиксированной длинны, то их объём, или объём «иссушенной» зоны был бы пропорционален r2 , и последний член в уравнении (1.50) следовало бы заменить на t.
Если бы выделение происходило бы в виде плёнки, то объём «иссушенной» области рос бы, как t1/2 и формула для c приняла бы вид c c0 ( t)1/2 .
Таким образом, форму выделений можно определить по начальному наклону кривой в координатах ln(c c0) t.
33

При анализе экспериментальных данных уравнение (1.50) часто заменяют эквивалентным экспоненциальным выражением. Функцию exp( x) можно разложить в ряд
exp( x) (1 x |
2x2 |
|
3x3 |
|
|
|
|
|
...), |
(1.51) |
|
|
3! |
||||
2! |
|
|
|
||
который сходится для всех x 1. Если x 1, первые члены (1 x) дают хорошее приближение. Сравнивая уравнения (1.50) и (1.51), для малых времён можно написать
|
|
|
|
2bt |
|
c |
c |
exp |
|||
3c2/3 |
|||||
0 |
|
|
|||
|
|
|
|
o |
|
3/2
|
|
|
t 3/2 |
|
|||
c |
0 |
exp |
|
|
, |
(1.52) |
|
|
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
где время релаксации дается следующим выражением:
|
c1p/3re2c02/3 |
|
|
cp |
1 |
|
|
||
|
r2 |
|
3 |
|
|
||||
|
|
|
e |
|
|
|
(1.53) |
||
|
|
|
|||||||
|
2D(c0 c ) |
|
|
|
. |
||||
|
2D c0 |
|
|
||||||
Время релаксации можно определить из данных по c(t). Обычно величины cp , c0 , c и D известны из других
экспериментов. Поэтому можно вычислить re и затем
истинное расстояние между частицами. Если растет, то скорость выделения уменьшается; таким образом, уравнение (1.53) указывает на параметры, с помощью которых можно менять скорость выделения.
При больших временах отжига концентрация растворенного вещества на границе ячейки меняется со временем и наилучшее приближение дает первый член
решения: |
|
|
|
|
|
|
|
|
|
An |
|
|
t |
|
|
|
|
|
|
|
|
(r). |
(1.54) |
|||
|
||||||||
c(r,t) c |
exp |
|
fn |
|||||
|
|
|
|
n |
|
|
||
34

Это решение применяют выделяющихся частиц (сферы, определить их форму из вида c(t нельзя.
независимо от формы прутки, плёнки), так что ) в этом интервале времени
1.6. Диффузия в поле упругих напряжений
Рассмотрим влияние градиента упругих напряжений на диффузию. Градиент потенциала создает поток атомов, который добавляется к концентрационному потоку в уравнении, где фигурирует полный поток.
Рассмотрим отдельную частицу, движущуюся в потенциальном поле U(x, y,z). Градиент потенциала есть сила
F , действующая на частицу:
F U . |
(1.55) |
Эмпирически установлено, что градиент потенциала или сила приводит к диффузионному перемещению атомов с некоторой скоростью, которая связана с силой следующим отношением:
V BF , |
(1.56) |
где B - подвижность диффундирующего атома. Следует отметить, что в этом уравнение сила не равна массе, умноженной на ускорение. Здесь сила приводит к возникновению постоянной скорости вместо ускорения, так как атомы всё время меняют направлении е движения и поэтому не могут ускоряться под действием силы, как свободные частицы.
Подвижность атомов пропорциональна коэффициенту диффузии D. Далее будет показано, что соотношение между ними имеет вид:
B |
D |
, |
(1.57) |
|
|||
|
kT |
|
|
35
где k - постоянная Больцмана, а T - абсолютная температура.
Поток, возникающий в однородной системе под действием F , равен средней скорости частицы, умноженной на число частиц в единице объёма, т.е.
|
|
|
|
||
J cV |
BFc |
Dc |
U . |
(1.58) |
|
|
|||||
kT
Если градиент концентрации существует вдобавок к U , то в первом приближении уравнение для потока есть сумма уравнений (1.1) и (1.58):
|
|
|
c U |
|
|
J |
D |
c |
|
. |
(1.59) |
|
|||||
|
|
|
kT |
|
|
Подставляя это уравнение потока в уравнение непрерывности (1.6), для постоянного значения D получим:
c |
|
|
c U |
|
|
|
D |
c |
|
. |
(1.60) |
t |
|
||||
|
|
kT |
|
||
Чтобы найти c(x, y,z,t) при наличии градиента потенциала, надо решить это уравнение.
Рассмотрим вначале решение для очень малых времён. Известно, что поле напряжений, возникающее вокруг
внедрённого атома в твёрдом растворе, способствует его
притяжению к дислокации. |
Поэтому в |
однородном |
( c 0) пересыщенном сплаве |
возникает |
диффузионное |
движение избыточных атомов к дислокациям. При этом возникнет и концентрационная неоднородность. Скорость выделения на дислокациях будет расти благодаря наложению на дрейф в поле напряжений движения под действием градиента концентрации. Обозначим через r - расстояние между внедренным атомом и ядром линейной или винтовой дислокации. Взаимодействие между ними в цилиндрической системе координат определяется потенциалами вида:
36
U(r, ) |
|
(для винтовой дислокации). |
(1.61) |
||
|
|
||||
|
|
r |
|
||
U(r, ) |
A |
sin (линейная дислокация), |
(1.62) |
||
|
|||||
|
|
r |
|
||
где и A - константы.
Если сплав гомогенизирован при высокой температуре и закален, в результате чего он становится пересыщен, то начальное распределение для изолированной дислокации имеет вид
|
|
c c0 |
при r 0,t 0. |
|
||||
Теперь уравнения (1.60) |
можно записать как |
|
||||||
|
c |
D 2c |
D c U |
|
Dc 2U |
. |
(1.63) |
|
|
|
kT |
|
|||||
|
t |
|
|
kT |
|
|||
Начальный поток атомов к изолированной дислокации зависит как от c , так и U . Но, в отличие от c , градиент потенциала U не зависит от времени. При решении уравнения (1.63) учтём, что в однородном сплаве при t 0,
c 0 и, следовательно, |
2c 0, так что |
c |
определяется |
|
|||
|
|
t |
|
только последним членом уравнения (1.63). Выражение для2U(r, ) в цилиндрических координатах имеет вид
2 |
|
2U 1 U |
|
1 2U |
|||||||
U(r, ) |
|
|
|
|
|
|
|
|
|
|
. |
|
r2 |
r |
r |
r2 |
2 |
||||||
Если U(r, ) задается |
уравнением (1.62), то 2U 0 и |
||||||||||
c |
0 . Если уравнением (1.61), то |
2U 0. Следовательно, |
|
||
t |
|
|
диффузия отсутствует в упругом поле краевой дислокации и идёт в упругом поле винтовой. Если читатель знаком с теорией дислокаций, то этот вывод должен его поразить.
37

Для малых времен изменение концентрации в зависимости от времени таково, что градиент концентрации очень медленно достигает заметной величины, поэтому распределение растворенных атомов к дислокации можно удовлетворительно описать, предположив что c 0. Для винтовой дислокации градиент упругого потенциала равен
U . r2
Этот градиент заставляет растворенные атомы двигаться к дислокации со скоростью, которую можно определить как:
V(r) |
dr |
|
D |
|
|
. |
(1.64) |
|
|
|
|||||
|
dt |
kT r2 |
|
||||
Интегрируя это выражение от r r при t 0 до r 0 при t t , получим
1
3D t 3
r . (1.65)
kT
Объяснить полученное выражение можно следующим образом. Атомы, которые вначале находились на расстоянии r от ядра дислокации, подходят к нему в момент времени t t , а другие растворённые атомы, находившиеся в начале в
области |
r r , |
заняли места |
у r r . Поэтому, |
хотя |
|
c |
|
|
t |
||||||
|
|
|
|
t t |
|
||
остается равным нулю, в момент времени |
всё |
||||||
растворённое вещество, находившееся в области |
r r |
при |
|||||
t 0, |
должно |
выделиться |
или сегрегировать |
у |
ядра |
||
дислокации.
Количество перемещённого вещества q на единицу длины дислокации, к моменту t определяется по формуле:
38
|
|
|
|
3D t |
2 |
|
|
|
q c r |
2 |
|
3 |
|
|
|||
|
c |
|
|
. |
(1.66) |
|||
|
kT |
|||||||
0 |
|
0 |
|
|
|
|
|
|
Период, в течение которого это решение применимо, определяется объёмом, в пределах которого потенциал оказывает заметное воздействие на растворенные атомы. Точнее: тепловая энергия растворенного атома в решётке порядка kT , поэтому, когда r становится настолько большим, что U(r) kT (т.е. потенциальная энергия частицы меньше тепловой), то влиянием потенциала можно пренебречь. Таким образом, можно определить эффективный радиус действия потенциала r R, на котором
|
|
|
|
U(R) kT |
|
. |
(1.67) |
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
Таким образом, |
условие |
|
c |
0 |
сохраниться дольше в |
||||||||
|
|
||||||||||||
области |
r R , |
где |
влияние |
|
t |
велико по сравнению |
с |
||||||
U |
|||||||||||||
областью |
r R . |
Эти выводы |
|
можно |
применить только |
по |
|||||||
отношению |
к |
|
растворённому |
|
веществу, |
вначале |
|||||||
находившемуся |
в |
районе r R . |
В момент времени, когда |
||||||||||
r R, появляются заметные концентрационные градиенты и
требуется другой подход к задаче. |
|
|
Значение R для |
случая углерода в α-железе |
можно |
оценить по величине |
. Принимая 10 21н/ м2 , получим |
|
R 25 10 10 м . При плотности дислокации порядка |
1015 м 2 |
|
расстояние между ними составляет примерно 3 10 8 м . Даже при такой относительно высокой плотности дислокации уравнение (1.66) не выполняется после выделения небольшой доли растворённого вещества.
Чтобы изучать процесс выделения при более продолжительных временах, предположим, что действительное расположение дислокации можно заменить параллельными их рядами, расстояние между которыми такое
39

же, как истинное. Поступая по аналогии с ранее рассмотренной задачей о кинетике выделений, проведем плоскости посредине между каждой парой дислокации и параллельно им. Каждая дислокация окажется в ячейке с «непроницаемыми» стенками. Задача сводится к нахождению c(t) в одной из этих ячеек. Рассмотрение было бы близко к сферическому случаю, если бы не появлялся потенциал вокруг дислокации.
Рассмотрим стадию выделения, на которой R r но re 2
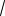 Dt . Чтобы рассчитать потоки внутри области r R , необходимо решить уравнение (1.63). Однако нас интересует в основном не c(r, ,t), а скорость «откачки» растворённого вещества из пересыщенного раствора. Решение уравнения (163) относительно c можно избежать, если известно, что каждый атом, входящий в область r R , будет втягиваться в ядро со все возрастающей скоростью. Другими словами, любой растворённый атом, попавший в область r R , будет «захвачен» потенциальным полем, которое необратимо толкает его к дислокации. Поэтому стоит только растворенному атому попасть в эту область, то он уходит из раствора, как если бы произошло выделение. Упрощение, таким образом, делается очевидным: задачу нахождения c(r,t) при U 0 можно обойти, выбрав специфическое граничное условие:
Dt . Чтобы рассчитать потоки внутри области r R , необходимо решить уравнение (1.63). Однако нас интересует в основном не c(r, ,t), а скорость «откачки» растворённого вещества из пересыщенного раствора. Решение уравнения (163) относительно c можно избежать, если известно, что каждый атом, входящий в область r R , будет втягиваться в ядро со все возрастающей скоростью. Другими словами, любой растворённый атом, попавший в область r R , будет «захвачен» потенциальным полем, которое необратимо толкает его к дислокации. Поэтому стоит только растворенному атому попасть в эту область, то он уходит из раствора, как если бы произошло выделение. Упрощение, таким образом, делается очевидным: задачу нахождения c(r,t) при U 0 можно обойти, выбрав специфическое граничное условие:
c c |
|
при r R, |
t 0 |
|
Теперь задача сводится к обычной диффузионной без всякого потенциала и может быть решена способом, аналогичным для сферических выделений.
1.7. Решение для переменного значения коэффициента диффузии
В реальных экспериментах величина коэффициента диффузии D не является константой. Даже для одного и того
40
