
Технология изготовления полосовых и режекторных фильтров с использованием ПАВ и MEMS-структур. Андреев И.В., Андреев А.И
.pdf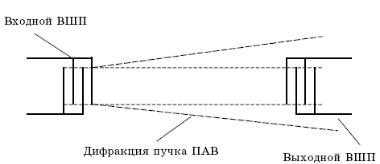
автоколлимации. В большинстве случаев этот эффект является желательным явлением в акустоэлектроннных устройствах. Автоколлимация важна для устройств с протяженными электродными структурами и для линий задержки с большим временем задержки, так как приводит к уменьшению дифракционных потерь. Степень дифракции для каждого конкретного пьезоэлектрического материала фиксирована. В монокристаллах дифракционное расширение акустических пучков оценивается параметром анизотропии γ. Величина и знак γ определяют степень дифракции поверхностных волн. В изотропной среде γ = 0; при γ > 0 дифракционные потери больше, чем в изотропной среде, при γ < 0 потери меньше, чем в изотропной среде.
Если γ = –1, в анизотропной среде наблюдается автоколлимация, при которой расширение акустического пучка минимальное или отсутствует. С точки зрения дифракционных эффектов идеальным является материал со значением γ близким к –1 /2/. Ниже приведены значения параметра анизотропии γ для некоторых материалов.
Рис. 18. Дифракция пучка ПАВ, излученных ВШП
Кроме расширения акустического пучка изменяются и профили интенсивности акустических волн по мере удаления от излучателя (рис. 18). Дифракционная картина ПАВ, распространяющейся в анизотропной среде полностью определяется значением волнового параметра
41

F z(1 )/W 2 |
, |
(68) |
0 |
|
|
где – длина волны; z – расстояние от преобразователя до точки наблюдения; W0 – апертура преобразователя. Значение F
< 1 соответствует зоне Френеля (или ближней зоне), значение F > 1 отвечает дальней зоне. В зоне Френеля акустический луч не расходится, и профили ПАВ имеют вид близкий к прямоугольному, а энергия ПАВ сосредоточена в полосе, «освещаемой» апертурой входного аподизованного преобразователя (рис.19).
Рис. 19. Схематическое представление профилей ПАВ, распространяющихся по монокристаллической подложке
Значение F > 1 соответствует зоне Фраунгофера (или дальней зоне), в которой профили ПАВ принимают вид одногорбной кривой и акустический луч размывается. Очевидно, что для того чтобы вся акустическая энергия,
42
излученная входным преобразователем, была принята выходным, преобразователи должны быть расположены в ближней зоне друг относительно друга. Выбирая апертуру преобразователя, необходимо учитывать возможные дифракционные потери, связанные с расходимостью акустического луча, ограниченной апертуры. Поэтому апертура электродов ВШП не должна быть меньше значения, определяемого границей зоны Френеля:
W0 > λ/L0 + γ, |
(69) |
где γ – параметр анизотропии; |
L0– длина пути распространения |
ПАВ. Так, для ниобата лития YZ-среза γ = –1,083, для кварца
STсреза γ = +0,378 /2/.
3.3. Влияние подтрава на частотные характеристики фильтров на поверхностных акустических волнах
Влияние подтрава рассмотрено в работах /1, 2/. При этом следует учитывать, что между импульсной характеристикой ВШП h(nT0 ) и частотной характеристикой существует связь.
При представлении ВШП в виде трансверсального фильтра его передаточная функция имеет вид
N |
|
H0 jf Ane j2 fnT0 , |
(70) |
n 1 |
|
где T0 – дискретизации или временной интервал между выборками;
Аn – весовые коэффициенты, которые в общем случае являются периодической функцией с периодом fm, равным fm = 1/T0. Частота fm является предельной частотой. Передаточная функция трансверсального фильтра с идеальным полосовым фильтром на выходе не равна нулю только в полосе ширинойF, поэтому для спектральной плотности имеем /2, 3/
H jf |
H0 jf |
|
1 |
N |
A e j2 f0T , |
(71) |
|
|
|
||||
|
F |
|
n |
|
||
|
F n 1 |
|
|
|||
при f0 – F/2 f f0 + F/2 и вне области H(f) = 0.
Величина импульсного отклика фильтра определяется
43
путем обратного преобразования Фурье от спектральной плотности
|
|
|
|
|
|
|
|
|
|
h t H jf e j2 f0tdf . |
|
|
|
(72) |
|||
|
|
|
|
|
|
|
|
|
Откуда следует, что при отсутствии идеального фильтра |
||||||||
h t |
|
N |
A e j2 f t nT0 df |
N |
A t nT . |
(73) |
||
|
|
|
||||||
|
n |
n |
0 |
|
||||
|
n 1 |
|
n 1 |
|
|
|
||
А при учете трансверсального фильтра с идеальным полосовым фильтром
|
|
|
f0 |
|
F |
|
|
|
|
|
|
|||
|
|
1 |
2 N |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
h t |
|
|
|
|
|
Ane j2 f t nT0 |
|
(74) |
||||||
F |
||||||||||||||
|
|
F n 1 |
|
|
|
|
||||||||
|
|
|
f0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
N |
sin F t nT |
j2 f t nT |
|
|
|
|||||||||
An |
|
|
|
0 |
e |
0 |
|
. |
|
|||||
|
F t nT |
|
|
|
||||||||||
n 1 |
|
|
|
0 |
|
|
|
|
|
|||||
В соответствии с теоремой Шеннона любой сигнал вида s(t)= s0(f)ej t можно представить из одинаково удаленных в общем случае комплексных выборок:
sn = s(tn) = s(nT0) при условии T0 < 1/ F.
Тогда после подстановки t = tn = nT0 в формулу (9) получаем выражение для весовых коэффициентов
An = h(nT0), (75)
которые представляют выборки импульсного отклика комбинации трансверсального с идеальным полосовым фильтром. Для импульсного отклика следует, что
An s nT cos2 f0nT0 |
(76) |
||||
и временного интервала между выборками можно записать |
|||||
T |
Tv |
|
1 |
, |
(77) |
0 |
Nv |
Nv fv |
|
||
где Nv – число выборок за период; fv = 1/Tv – частота выборок.
Тогда для предельной частоты можно записать fm = 1/T0.
44
При умножении импульсной характеристики на некоторую весовую функцию W(t) имеем с ее подстановкой при t = tn
An = h0(tn)W(tn). |
(78) |
Согласно методу преобразования Фурье /6/ для |
|
симметричной АЧХ имеем передаточную функцию |
|
H( jf ) H ( j(2f f0 ), |
(79) |
где H*(j(2f–f0))– представляет комплексно-сопряженную величину.
Тогда импульсный отклик в соответствии с обратным преобразованием Фурье равен
|
f0 |
|
|
||
h t 2e j2 f0t |
Re H jf e j2 f f0 t dt, |
|
(80) |
||
f0 |
F |
|
|
|
|
|
|
|
|||
Амплитуда |
2 |
импульсного |
отклика |
является |
|
|
|
||||
действительной величиной, а положение электродов определяется формулой:
tn n T0 |
n |
|
n |
(81) |
Nv fv |
2f0 |
|
в данном случае период дискретизации T0 =1/2f0, который получается при числе выборок Nv = 2 и fv = f0. В этом случае весовые коэффициенты с учетом умножения на весовую функцию принимают вид
An c h0 tn W tn cos2 fvt c 1 n h0 tn W tn , (82)
где c – нормировочный множитель.
При другом числе выборок величина An не является действительной величиной. Влияние подтрава проявляется в изменении положения значений импульсной характеристики и положения ширины отдельного электрода. При этом следует учитывать, что исходными данными для учета подтрава являются эффективная скорость ПАВ e и значения
импульсной характеристики h0(tn)W(tn). Тогда для аподизованного ВШП1 имеем координаты
45
y |
y |
0 |
W(t |
n |
)h(t |
n |
) ( 1)n |
, |
|
|
(83) |
||
1 |
|
|
|
|
|
|
|
|
|
|
|||
y2 |
y0 |
W(tn )h(tn ) ( 1)n y , |
|
|
(84) |
||||||||
. |
e 0(2 k2 )/(2 k2 (dn 1)) , |
|
|
(85) |
|||||||||
|
|
Координаты левого и правого краев электродов равны |
|||||||||||
Xnp |
e (n dn )/ fe |
0.5 b , |
|
|
(86) |
||||||||
Xnp |
e (n dn )/ fe |
0.5 b , |
|
|
(87) |
||||||||
Для неаподизованного ВШП2 имеем координаты по оси Y: |
|||||||||||||
y1 y0 |
W0h(nT0 ), |
|
|
|
|
(88) |
|||||||
y2 y0 |
W0h(nT0 ) y b, |
|
|
(89) |
|||||||||
|
|
где h(nT )=( 1)n , W - апертура ВШП2, |
y |
0 |
- расстояние |
||||||||
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
от |
|
шины до |
верхнего |
или нижнего края |
электрода, y - |
||||||||
расстояние разрыва электрода. Другие координаты ВШП2 определяются аналогичными выражениями (86-87). Таким образом, влияние подтрава bпроявляется в изменении положения значений импульсной характеристики для каждого электрода и положения ширины электрода, что меняет передаточную характеристику отдельного преобразователя и всего фильтра в целом.
3.4. Изменение угловой ориентации взаимного расположения преобразователей и ее связь с частотными характеристиками фильтров и резонаторов
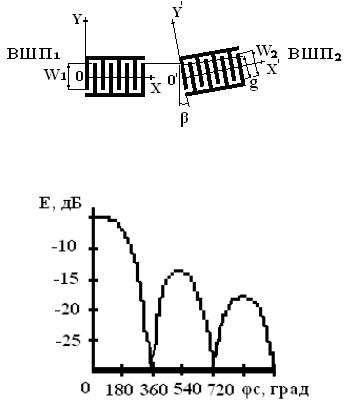
Рассмотрим влияние ошибок угловой ориентации взаимного расположения преобразователей на частотные характеристики фильтров и резонаторов. При этом надо учитывать, что кроме разооринтации срезов звукопроводов искажения частотных характеристик вызывают погрешности, определяемые взаимным расположением преобразователей. Эти погрешности могут возникать при мультиплицировании преобразователей фильтров или резонаторов с различных парциальных шаблонов, и приводит к искажению фронта излучаемых ПАВ, а также к энергетическим потерям. На рис.20
46
показано расположение приемного ВШП2, повернутого на угол β и смещенного на величину g cosβ относительно фронта однородной ПАВ, излученной ВШП1. Для анализа удобно использовать новую систему координат X1O1Y1, повернутую на угол β относительно основной системы XOY. В новой системе координат набег фазы в y1 –й точке ВШП2 составляет:
|
(y1) (2 / )(y1 y)sin . |
|
|
|
|
(90) |
|||||||||||
|
В результате АЧХ фильтра с двумя преобразователями. |
||||||||||||||||
один из которых повернут на угол β принимает вид /2/: |
|
||||||||||||||||
H( ) 2H |
|
|
( ) H |
|
( )cos( ) 2 |
(W /W )( |
1 |
(1 cos |
|
)), (91) |
|
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
2 |
|
c |
1 |
2 |
2 |
c |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
где |
H1 ( ), |
H2 ( ) ,W1 и W2соответственно |
|
АЧХ |
и |
||||||||||||
апертуры преобразователей 1 и 2, |
|
|
|
|
|
|
|||||||||||
c |
1 |
|
g |
, g |
– |
|
часть |
апертуры |
ВШП2, погруженный |
в |
|||||||
|
|
|
|||||||||||||||
|
W1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
акустический луч |
ширина W1, а угол |
|
|
|
|
|
|
||||||||||
c |
2 |
c W1 |
sin . |
|
|
|
|
|
|
(92) |
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ этого выражения показывает, что множитель W1/W2 определяет потери, связанные с различием апертур передающего и приемного преобразователей. множитель W1cosβ является эффективной апертурой преобразователя ВШП2 и характеризует потери, вызванные угловой
разоориентацией |
последнего, |
множитель |
c |
1 |
g |
|
|||||
|
|
|
|
W1 |
|
определяет потери, обусловленные , смещением ВШП2 относительно центральной оси излучения ПАВ, функция
E |
2 |
(1 cos c ), |
(93) |
|
|||
|
c |
|
|
график которой, показан на рис. 2 и обращается в нуль приc 2 m, m=1, 2, 3…n и связана с фазовыми ошибками,
47
вызванными разворотом ВШП2 относительно фронта принимаемой волны
Рис. 20. Расположение преобразователей ВШП1 и повернутого приемного ВШП2
Рис. 21. Зависимость функции E от угла φс
Учет этой функции позволяет определить влияние разоориентации на параметры частотных характеристик фильтров.
3.5. Применение вероятностного метода для оценки влияния погрешности ПАВ-структур преобразователей
Отклонения частотных характеристик фильтров могут быть связаны с применением вероятностного метода для
48
оценки влияния погрешности ПАВ-структур преобразователей, представленные в работах.
При этом следует учитывать, что вероятностный метод дает не только несколько расширенное поле допуска, но и позволяет определить характер влияния частных погрешностей.
Поэтому для обобщения рассмотрим основные расчеты допусков по вероятностному методу.
С учетом технологических погрешностей передаточная функция фильтра ПАВ, состоящего из двух преобразователей: одного полосозадающего (аподизованного) ВШП и другого широкополосного, записывается в виде
An |
|
|
2 |
|
|
|
H( j ) H2 ( ) qn (Ф(n) Ф(n)) exp(-j |
|
(xn xn )) (94) |
||||
|
|
|||||
n 1 |
|
|
e |
|
||
где H2( )-передаточная функция широкополосного |
||||||
преобразователя,qn - |
коэффициент |
определяющий |
число |
|||
дефектных электродов |
An |
в топологии полосозадающего |
||||
ВШП, Ф(n), xn , |
- |
погрешности |
длины, |
периода |
||
(расположения) электродов и скорости ПАВ соответственно. Длина электродов yn изменялась пропорционально функции аподизации Ф(n) h(tn ) w(tn ), полученной по методу прямой свертки импульсной характеристики h(tn ) преобразователя с различными весовыми коэффициентами w(tn ). Считая, что
передаточная функция фильтра определяется аподизованным ВШП, получим
An |
xn |
An |
xn |
|
|
H( j ) Hп ( ) (Ф(n)cos( |
) j (Ф(n)sin( |
), (95) |
|||
e |
|
||||
n 1 |
n 1 |
e |
|||
получаем уравнение функции влияния скорости ПАВ на АЧХ фильтра
49
|
|
|
2A Ln |
|
An An |
|
|
|
xn xm |
|
|
|
|
|||||||
TV |
( ) |
|
|
(Ф(n)(Ф(m)sin( |
) |
|
|
(96) |
||||||||||||
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
A ( ) e n 1 m 1 |
|
e |
|
|
|
|
|
|||||||||||
Для функции влияния периода электрода 2Ln |
ПАВ-структур, |
|||||||||||||||||||
т.е. положения xn |
|
электродов |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Ф(n) xn |
|
An An |
|
|
|
xn xm |
|
|
|
|||||||
Tx |
( ,n) |
|
(Ф(n)(Ф(m)sin( |
). |
|
(97) |
||||||||||||||
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
A ( ) e |
n 1 m 1 |
|
|
|
|
e |
|
|
|||||||
Для функции влияния длины электродов ПАВ-структур |
|
|||||||||||||||||||
|
|
|
|
|
Ф(n) |
|
An An |
xm |
|
|
|
|
|
|
|
|||||
Ty |
( ,n) |
|
(Ф(n) cos( |
xn |
), |
|
|
|
|
(98) |
||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
A ( ) n 1 m 1 |
e |
|
|
|
|
|
|||||||||
|
где |
|
|
2Ln -номинальное |
значение |
периода, |
||||||||||||||
Ф(m)соответствует при изменении индекса |
|
n на m. |
Расчет |
|||||||||||||||||
производственных допусков производится вероятностным методом и получается уравнение для расчета половины поля допуска для АЧХ
фильтра при условии отсутствия корреляционных связей
|
A( ) |
|
1 |
|
|
|
|
|
V |
A |
|
xn |
|
|
( |
|
(TV |
( )KV |
( |
) ((Tx ( ,n)Kx ( |
))2 |
||||||||
|
|
|
|
|||||||||||
|
A( ) Kn |
|
|
|
|
V n 1 |
|
xn |
||||||
|
A |
|
yn |
|
|
|
|
A |
||||||
((Ty ( ,n)Ky ( |
))2 )1/2 t0 (TV ( ) f |
l ((Tx ( ,n)+ |
||||||||||||
|
||||||||||||||
n 1 |
|
yn |
|
|
|
n 1 |
||||||||
|
A |
|
|
|
|
|
|
|
|
|
||||
l Ty ( ,n)) |
|
|
|
|
|
|
(99) |
|||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
||||
где Kn = коэффициент относительного рассеяния выходных параметров,KV , Kx , Ky - коэффициенты относительного
50
