
Учебное пособие 1699
.pdf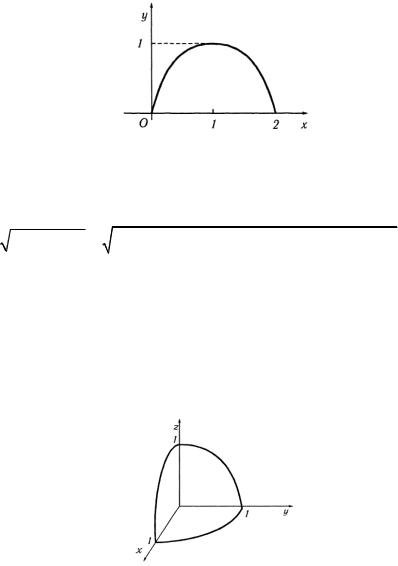
Рис. 1.37
в) Представим область интегрирования на рис. 1.38. Нетрудно заметить, что она займет первый октант единичного шара. Переходя к сферической системе координат, подынтегральная функция будет равна
x2 + y2 + z2 = (ρ sinθ cosϕ)2 +(ρsinθ sinϕ)2 +(ρ cosθ )2 = ρ
Таким образом, пользуясь формулой (6) и расставляя пределы интегрирования, будем иметь
π π
I = ∫∫∫ρ ρ2 sinθd ρdϕdθ = ∫2 sinθdθ∫2 dϕ∫1 ρ3d ρ =
G |
|
|
|
|
|
0 |
0 |
0 |
|
|
π |
π |
|
|
π |
|
|
= |
1 |
∫2 sinθdθ∫2 |
dϕ = |
π |
∫2 sinθdθ = |
π . |
||
|
4 |
0 |
0 |
|
8 |
0 |
|
8 |
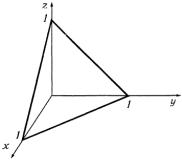
Рис. 1.38 |
|
|
6.2. Вычислить интегралы: a) ∫∫∫V |
dxdydz |
, где V - |
(x + y + z +1)3 |
||
область, ограниченная координатными плоскостями и
51
плоскостью |
x + y + z =1; б) ∫∫∫dxdydz , |
где |
V |
– |
область |
|
|
|
V |
|
|
|
|
ограниченная поверхностями |
x2 + y2 + z2 = 2Rz, x2 + y2 = z2 и |
|||||
содержащая |
точку (0, 0, R); |
в) ∫∫∫zdxdydz |
где |
V |
- |
область, |
|
|
V |
|
|
|
|
ограниченная конусом x2 + y2 = z2 т плоскостью z = h .
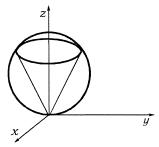
Решение. а) Область интегрирования показана на рис.
1.39.
Рис. 1.39
Расставим пределы интегрирования
|
dxdydz |
1 |
1−x |
1−x−y |
dz |
|
|
|
I = ∫∫∫ |
|
= ∫dx ∫ dy |
∫ |
|
. |
|||
(x + y + z +1) |
3 |
(x + y + z +1) |
3 |
|||||
V |
0 |
0 |
0 |
|
|
|||
Полагая х и у постоянными величинами, вычисляем внутренний интеграл по z
|
|
1 |
1 |
|
1−x |
|
|
|
|
1 |
|
|
|
|
1−x−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I = − |
|
∫0 dx ∫0 |
|
|
|
|
|
|
dy = |
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
(x + y + z +1)2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
1 |
|
1−x |
|
|
|
|
|
1 |
|
|
|
1 |
1 |
y |
|
|
1 |
|
|
|
1−x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= − |
|
dx |
1 |
− |
|
|
|
|
|
dy |
= − |
|
+ |
|
|
|
dx = |
|||||||||||
2 |
|
|
|
|
|
|
|
2 |
2 |
4 |
x + y +1 |
|||||||||||||||||
|
∫0 |
|
|
∫0 4 |
|
|
(x + y +1) |
|
|
|
∫0 |
|
|
|
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 1 |
|
1 |
(1− x) |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|||||
= − |
|
∫0 |
|
|
+ |
|
− |
|
|
dx = |
ln 2 − |
|
|
. |
|
|
|
|||||||||||
|
|
|
|
x +1 |
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
8 |
|
|
|
|
|
|
|||
52
б) Преобразуя уравнение сферы к виду x2 + y2 +(z − R)2 = R2 , нетрудно заметить, что центр сферы
смещен по оси z на R. Таким образом, область интегрирования ограничена сверху сферической, а снизу конической поверхностью (рис. 1.40). Искомый интеграл в сферической системе координат примет вид
I = ∫∫∫dxdydz = ∫∫∫ρ2 sinθd ρdθdϕ .
V G
Рис. 1.40
Подставляя в уравнение сферы сферические координаты,
будем |
иметь |
|
ρ = 2R cosθ . |
|
|
Расставляя |
пределы |
||
интегрирования, получим |
|
|
|
|
|||||
|
|
π |
|
|
|
|
π |
|
|
I = |
2∫π dϕ∫4 sinθdθ |
2R∫cosθ ρ2d ρ = 8R3 2∫π dϕ∫4 cos3 θ sinθdθ = |
|||||||
|
0 |
0 |
|
|
0 |
3 |
0 |
0 |
|
|
8R3 |
|
π |
2∫π dϕ =πR3. |
|
|
|
|
|
= − |
cos4 θ |
4 |
|
|
|
|
|||
|
3 4 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) Проекция конуса на плоскость Оху есть круг х2 + у2 = h2 (рис. 1.41). Расставляя пределы интегрирования в тройном интеграле, будем иметь
|
h |
2 |
|
2 |
|
1 |
2π |
2 ρ2 |
|
ρ4 |
|
|
h |
h4π |
|
|
|
|
|
|
|
|
|||||||||||
I = ∫∫dxdy∫(h |
|
− p |
|
)ρd ρ = |
|
∫ h |
|
|
− |
|
|
|
= |
|
. |
|
|
|
2 |
2 |
4 |
4 |
|||||||||||
S |
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
53
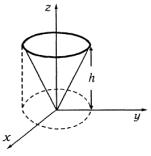
Рис. 1.41
1.7. Вычисление величин посредством тройного интеграла
1°. Объем тела, занимающего область V, в декартовой системе координат определяется по формуле
V = ∫∫∫dxdydz . |
(1) |
V |
|
Масса тела, занимающего область V, определяется по формуле
m = ∫∫∫δ (x, y, z)dxdydz , |
(2) |
где δ (x, y, z) - плотность тела в точке (x,y,z).
2°. Статические моменты тела относительно координатных плоскостей вычисляются по формулам
mxy = ∫∫∫δ (x, y, z)zdxdydz;
|
|
V |
|
|
|
|
|
|
|
|
|
|
mxz = ∫∫∫δ (x, y, z)ydxdydz; |
(3) |
|||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
myz = ∫∫∫δ (x, y, z)xdxdydz. |
|
|||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
Координаты центра тяжести тела |
|
|
|
|||||||||
x = |
myz |
; y |
c |
= |
m |
xz |
; z |
c |
= |
mxy |
, |
(4) |
|
|
|
|
|||||||||
c |
m |
|
|
m |
|
m |
|
|
||||
|
|
|
|
|
|
|
|
|||||
где m - масса тела.
54

3°. Моменты инерции тела относительно координатных
осей
I |
x |
= |
∫∫∫ |
δ (x, y, z) |
( |
y2 + z2 |
dxdydz; |
|
|
|
|
|
) |
|
|||
|
y |
|
V |
|
( |
|
) |
|
I |
|
∫∫∫ |
δ (x, y, z) |
x2 + z2 |
(5) |
|||
|
= |
|
|
dxdydz; |
||||
|
|
|
V |
|
( |
|
|
|
I |
z |
= |
∫∫∫ |
δ (x, y, z) |
x2 + y2 |
dxdydz. |
|
|
|
|
|
|
) |
|
V
4°. Моменты инерции относительно координатных плоскостей
Ixy = ∫δ (x, y, z)z2dV ;
V |
|
Ixz = ∫δ (x, y, z)y2dV ; |
(6) |
V |
|
Iyz = ∫δ (x, y, z)x2dV , |
|
V |
|
где dV= dxdydz. |
|
Полярный момент инерции равен |
|
I0 = Ixy + Ixz + Iyz = ∫δ (x, y, z)(x2 + y2 + z2 )dV . |
(7) |
V
5°. Если в теле объема V непрерывным образом распределены массы с заданной в каждой точке М (x,y,z) плотностью
δ (M )=δ (x, y, z), ТО проекции на оси координат полной силы
притяжения FG на точку A(xc,yc,zc), в которой, мы считаем, сосредоточена единица массы, согласно закону притяжения Ньютона, определяются по формулам
Fx = ∫ x −3xc δdV ; Fy = ∫ y −3yc δdV ; Fz = ∫ z −3zc δdV , (8) |
|||||
V |
r |
V |
r |
V |
r |
где r = (x − xc )2 +(y − yc )2 +(z − zc )2 - расстояние МA.
6°. Ньютоновское поле потенциально. Выражение для потенциала поля тела объема V с плотностью δ на точку А имеет вид
55

W = ∫δdV |
(9) |
|
V |
r |
|
Если тело однородно, то в приведенных формулах следует положить δ (x, y, z)=1.
7.1. Найти объем тела, ограниченного поверхностями:
а) z = x2 + y2 , z = x2 +2y, y = x, y = 2x, x =1;
б) x2 + y2 = z2 , x2 + y2 + z2 = a2 , внутри конуса;
|
2 |
2 |
2 |
|
|
|
||||
в) (x2 + y2 + z2 )2 = a3 x; |
г) |
x |
|
+ |
y |
+ |
z |
|
= xyz3 . |
|
2 |
|
2 |
2 |
|
||||||
|
|
a |
|
|
b |
|
c |
h |
|
|
Решение. а) Объем тела в декартовой системе координат |
||||||||||
определяется по формуле |
|
|
|
|
|
|
|
|
||
|
V = ∫∫∫dxdydz . |
|
||||||||
|
|
|
|
V |
|
|
|
|
|
|
Тело сверху и |
|
снизу |
ограничено |
параболлойдами |
||||||
z = x2 + 2 y2 и z = x2 + y2 . |
Проекция |
тела на |
плоскость Оху |
|||||||
показана на рис. 1.42. Расставляя пределы интегрирования, получим
1 |
2 x |
x2 +2 y2 |
1 |
2 x |
|
1 |
1 |
|
7 |
|
|||
V = ∫dx ∫dy |
|
∫ |
|
dz = ∫dx ∫ |
y2dy = |
∫7x3dx = |
|
. |
|||||
2 |
2 |
3 |
12 |
||||||||||
0 |
x |
+y |
0 |
x |
|
0 |
|
||||||
x |
|
|
|
|
|
|
|||||||
Рис. 1.42
б) Представим искомый объем на рис. 16.43. Поскольку тело, заключенное внутри конуса, симметрично относительно начала координат, то его объем в сферической системе координат равен
56
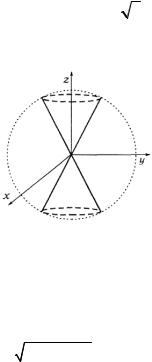
π
V = 2∫∫∫ρ2 sinθd ρdθdϕ = 22∫π dϕ∫4 sinθdθ∫a ρ2d ρ =
G |
|
|
|
|
|
|
0 |
|
0 |
0 |
|
2π |
|
|
π |
|
3 |
|
|
|
|
= − 2 a3 |
|
|
4 |
dϕ = 4πa |
|
2 |
||||
∫ |
cosθ |
|
|
|
1 |
− |
. |
|||
|
|
|
|
|||||||
3 |
|
|
|
3 |
|
|
|
2 |
|
|
0 |
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
Рис. 1.43
в) Поскольку уравнение содержит выражение х2 + у2 + z2, то целесообразно перейти к сферическим координатам
x = ρsinθ cosϕ, y = ρ sinθ sinϕ, z = ρ cosθ
Уравнение поверхности в сферической системе координат будет ρ = a 3 sinθ cosϕ .
Переменные y и z входят в уравнение только в квадратах, поэтому тело симметрично относительно плоскостей Oxz и Оху. Учитывая, что x ≥ 0 , т. е. все тело расположено в области положительных значений х, достаточно вычислить четвертую часть объема. В первом октанте в сферической системе
координат |
переменные |
изменяются |
в |
пределах |
0 ≤θ ≤ |
π |
, |
|
|
π . |
|
|
|
|
|
2 |
|
0 ≤ϕ ≤ |
Подставляя |
в формулу |
(1) |
значение |
якобиана |
|||
|
2 |
|
|
|
|
|
|
|
I = ρ2 sinϕ , получим
57

|
|
|
|
π |
|
|
π |
a 3 sinθ cosϕ |
|
|
π |
π |
|
|
V = 4∫2 dθ∫2 |
|
4a3 |
∫2 sin2 θdθ∫2 cosϕdϕ = |
|||||||
|
|
dϕ ∫ ρ |
2 sinθd ρ = |
|||||||||
|
|
|
|
0 |
0 |
0 |
|
3 |
0 |
0 |
||
|
|
|
|
π |
|
|
|
|
|
|||
|
|
= |
2a3 ∫2 (1−cos 2θ )dθ = |
πa3 . |
|
|
|
|||||
|
|
|
3 |
|
0 |
|
|
3 |
|
|
|
|
|
|
|
г) При наличии в |
уравнении поверхности выражения |
||||||||
|
x2 |
+ |
y2 |
+ |
|
z2 |
|
целесообразно перейти |
к обобщенным |
|||
|
a2 |
b2 |
|
c2 |
||||||||
|
|
|
|
|
|
|
|
|
||||
сферическим координатам |
|
|
|
|||||||||
|
|
|
|
x = aρsinθ cosϕ, y = bρsinθ sinϕ, z = cρ cosθ . |
||||||||
|
|
|
Якобиан в этом случае равен |
I = abcρ2 sinθ . Уравнение |
||||||||
поверхности в обобщенных сферических координатах имеет
вид ρ = abc sin2 θ cosθ sinϕ cosϕ . |
Учитывая симметрию и |
|||
h3 |
|
|
|
|
расставляя пределы интегрирования, будем иметь |
||||
π |
π |
abc sin2 |
θ cosθ sinϕcosϕ |
|
2 |
2 |
h3 |
∫ |
|
V =8∫dϕ∫dθ |
|
abcρ2 sinθd ρ = |
||
0 |
0 |
|
0 |
|
ππ
=8 (abc)4 ∫2 sin3 ϕ cos3 ϕdϕ∫2 sin7 θ cos3 θdθ = (abc)4 . 3 h9 0 0 180h9
7.2. Определить массу: а) пирамиды, ограниченной плоскостями x + y + z = a, х = 0, y = 0, z = 0, если плотность в каждой ее точке равна аппликате z этой точки; б) сферического слоя между поверхностями x2+y2+z2=R2 и х2 + у2 + z2 = 4R2, если плотность в каждой его точке обратно пропорциональна расстоянию точки от начала координат.
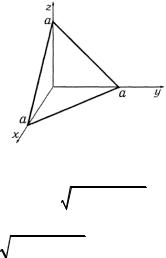
Решение. а) Пирамида показана на рис. 1.44. Поскольку по условию задачи плотность δ (x, y, z)= z , то, пользуясь формулой (2), будем иметь
58
|
|
|
a |
a−x |
a−x−y |
|
|
|
|
|
1 |
a |
a−x |
(a − x − y)2 dy = |
||||||
m = ∫∫∫zdxdydz = ∫dx ∫ dy |
∫ |
|
zdz = |
∫dx |
∫ |
|
||||||||||||||
|
|
V |
0 |
0 |
0 |
|
|
|
|
|
|
2 |
0 |
|
0 |
|
|
|
|
|
= |
1 |
a |
(a − x)2 y −(a − y)y2 + |
y |
3 |
|
a−x |
dx = |
1 |
a |
(a − x)3 dx = |
a |
4 |
|
||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
6 |
|
24. |
||||||||||||||
|
∫0 |
|
|
3 |
|
|
|
0 |
|
|
∫0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 1.44
б) Поскольку расстояние точки от начала координат
определяется выражением |
|
x2 + y2 + z2 то |
плотность |
будет |
||||||||||
равна δ (x, y, z) |
= |
|
1 |
|
|
. |
Пользуясь |
формулой |
(2) в |
|||||
x2 + y2 + z2 |
||||||||||||||
сферической системе координат, получим |
|
2∫R ρd ρ = |
|
|||||||||||
m = ∫∫∫ |
1 |
ρ2 sinθd ρdθdϕ = |
2∫π dϕπ∫sinθdθ |
|
||||||||||
|
|
|||||||||||||
G |
|
ρ |
|
|
|
|
|
|
0 |
0 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 R2 |
2∫π cosθ |
|
π |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
= − |
|
dϕ = 6πR2 . |
|
|
|
||||||||
|
|
|
|
2 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7.3. Найти координаты центра тяжести однородного тела, ограниченного поверхностями: х + у + z=1, х = 0, у = 0, z = 0.
Решение. Масса тела определяется по формуле (2)
1 |
1−x |
1−x−y |
1 |
1−x |
(1− x − y)dy = |
1 |
1 |
1 . |
m = ∫dx ∫ dy |
∫ |
dz = ∫dx ∫ |
∫(1− x)2 dx = |
|||||
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
6 |
По формулам (3) находим статические моменты
59

|
1 |
1−x 1−x−y |
|
1 |
1 |
1−x |
|
|
1 |
1 |
|
|
1 |
|
|
|||||||
mxy |
= ∫dx |
∫ |
dy |
∫ |
zdz = |
∫dx ∫ |
(1− x − y)dy = |
∫(1− x)3 dx = |
|
; |
||||||||||||
2 |
6 |
24 |
||||||||||||||||||||
|
0 |
|
0 |
|
0 |
|
|
0 |
0 |
|
|
0 |
|
|
||||||||
|
1 |
1−x |
|
1−x−y |
|
1 |
1−x |
|
|
1 |
|
1 |
|
1 |
|
|
|
|||||
mxz |
= ∫dx |
∫ |
ydy |
|
∫ |
dz = ∫dx ∫ |
y (1− x − y)dy = |
|
∫(1− x)3 dx = |
|
; |
|
||||||||||
|
|
6 |
24 |
|
|
|||||||||||||||||
|
0 |
|
0 |
|
|
0 |
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
||||
|
1 |
|
1−x |
1−x−y |
|
1 |
1−x |
|
1 |
1 |
|
1 |
|
|
|
|||||||
myz |
= ∫xdx |
∫ dy |
∫ |
dz = ∫xdx |
∫ (1− x − y)dy = |
∫(1− x)2 dx = |
|
. |
|
|||||||||||||
2 |
|
24 |
|
|||||||||||||||||||
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
||||||
Таким образом, по формулам (4) xc = yc = zc = 14 .
7.4. Найти координаты центра тяжести сферы x2 + y2 + z2 = 2az , если плотность в точках сферы обратно
пропорциональна расстоянию этих точек от начала координат. Решение. Центр сферы сдвинут по оси Oz на величину радиуса. По соображениям симметрии, очевидно, что хс и ус
равны 0.
По условию задачи плотность равна δ = |
1 |
|
, |
||||||||||
x2 + y2 + z2 |
|||||||||||||
тогда |
|
|
|
|
dxdydz |
|
|
|
|
|
|||
|
|
m = ∫∫∫ |
|
|
. |
|
|
|
|||||
|
|
x |
2 |
+ y |
2 |
+ z |
2 |
|
|
|
|||
|
|
|
V |
|
|
|
|
|
|
|
|||
Переходя к сферическим координатам и расставляя |
|||||||||||||
пределы интегрирования по V, будем иметь |
|
|
|
||||||||||
|
π |
|
|
|
|
|
|
π |
|
|
|
|
|
2π |
2 |
2acosθ |
|
|
2π |
|
2 |
|
|
|
2 |
|
|
m = ∫ dϕ∫sinθdθ |
∫ |
ρd ρ = 2a2 ∫ dϕ∫sinθ cos2 θdθ = 4πa |
. |
|
|||||||||
0 |
0 |
0 |
|
|
|
0 |
|
0 |
|
|
3 |
|
|
Статический момент относительно плоскости Оху по формуле (3) равен
60
