Учебное пособие 1604
.pdf
(1)– швеллер №14, по данным прил. 3: h1=140мм; b1=58мм; s=4.9мм; t=8.1мм; A1=15.6cм2; z0=1.67 см.
(2)– прямоугольник h2=7см; b2=13 см.
2. На рис. 3 укажем расположения собственных центральных осей простейших фигур. Площади простейших фигур: A1=15.6см2; А2=h2 b2=7 13=91cм2, с центрами тяжести в С1, C2 и центральными осями соответственно. Площадь всей фигуры A=A1+А2=15.6+91=106,6cм2.
В произвольной системе координат ZOY, показанной на рис. 3, определим координаты центров тяжести простейших фигур:
С1: |
yc1= |
= |
7.00см; |
zc1=b2-z0=13-1.67=11.33см |
|||
C2: |
yc2= + |
= |
17.50см; |
zc2= |
b2 |
= |
6.50см |
|
|||||||
|
|
|
|
2 |
|
|
|
3. Определим положение центра тяжести всей фигуры и ее центральных осей. Для этого найдем сначала значения статических моментов
Sy= zc1 |
A1 |
+ zc2 |
A2 =6.50 |
91.00+11.33 |
15.60=91.50+176.75=768.25 см3, |
|
Sz= yc 1A1 |
+ yc2 |
A2 =7.00 |
15.60+17.50 |
91.00=109.20+1592.50=1701.70см3 |
||
Тогда |
yc= |
|
= 15.96см |
zc= |
= 7.21см |
|
По полученным данным на рис. 3 отметим точку С и проведем через нее цен-
тральные оси |
, . |
|
|
|
Вычислим в этих осях координаты точек С1 и С2 по формулам (10): |
||||
С1: |
|
см |
C2: |
см |
|
|
см |
|
см |
Выполним проверку 1 правильности расчетов: |
|
|||
Syc= |
A1+ |
A2 = 4.12 15.60+( 0.71) 91.00= 64.27 |
64.61= 0.34 см3 |
|
Szc= |
A1+ |
A2 = 8.96 15.60+1.54 91.00= 139.78+140.14=0.36 см3 |
||
Погрешности допустимые, так как:
4. Вычисляем осевые и центробежный моменты инерции каждой простейшей фигуры относительно собственных центральных осей:
11
для фигуры (1) по табл. сортамента для швеллера (прил. 3) :
Jyc1=45.4cм4; Jzc1=491см4; |
а Jzc1yc1=0 в силу симметрии фигуры. |
для фигуры (2) по формулам из прил. 1:
Jyc2 = |
= |
= 1281.58см4; Jzc2 = |
= 371.58см4; Jzc2yc2=0. |
5. Вычислим осевые и центробежный моменты инерции всей фигуры относительно найденных центральных осей 
, 
:
Jyc=Jyc1+
A1+Jyc2+
A2
45.40+4.122
15.60+1281.58+(
0.71)2
91.00= =45.40+264.80+1281.58+45.87=1637.65см4
Jzc=Jzc1+ |
A1+Jzc2+ |
A2=371.58+(1.54)2 91.00+491.00+( 8.96)2 15.60= |
|
=371.58+1255.39+491.00+215.82=2330.79см4 |
|||
Jzcyc=Jzc1yc1+ |
A1+Jzc2yc2+ |
A2=0.00+1.54 (-0.71) 91.00+0.00+ |
|
+( -8.96) 4.12 15.60=99.50+575.88= |
675.38 см4 |
||
6.Найдем главные моменты инерции:
Jmax = |
Jzс+Jyс |
|
|
(Jzс-Jyс)2 |
2 |
= |
|
|
+ |
|
|
+(Jzсyc) |
|
||
2 |
4 |
|
|||||
|
|
|
|
|
|
||
1984.22+759.11=2743.33см4
Jmin = |
Jzс+Jyс |
|
|
(Jzс-Jyс)2 |
2 |
= |
|
|
- |
|
|
+(Jzсyc) |
|
||
2 |
4 |
|
|||||
|
|
|
|
|
|
||
Установим положение главных центральных осей инерции:
Jzcyc |
|
= |
1.64; αmax = 58.63 . |
tgαmax = Jzc-Jmax |
= |
Так как αmax > 0, то первая главная центральная ось 
инерции отклоняется от оси 
против хода часовой стрелки на угол 58.63 (рис.4).
Выполним проверку 2 правильности расчетов:
12
Jmax+ Jmin=2743.33+1225.11=3968.44см4, Jyc+ Jzc= 1637.65+2330.79=3968.44см4
погрешность допустимая, т.к. 
= 0.00
Jmax
Jmin=2743.33
1225.11= 3360881.02
Jyc
Jzc-J2zcyc=1637.65
2330.79 – (
675.38)2=3817018.24 - 456138.14 = 3360880.10
погрешность допустимая, т.к. 
=0.00
.
7. Построим главный центральный эллипс инерции в найденных осях. Для этого вычислим главные центральные радиусы инерции:
imax= |
5.07см |
imin= |
= 3.39см |
На рис. 4 изобразим заданную фигуру, главные центральные оси и главный центральный эллипс инерции, откладывая imax от оси 
, а imin- от оси
.
|
|
|
Yc |
i |
|
|
I |
max |
59° |
min=3,4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
Zc |
|
C |
|
|
|
|
|
|
max=5,07 |
|
|
|
|
|
i |
|
|
|
|
|
|
|
I |
min |
|
|
|
|
|
|
|
|
|
|
Рис. 4. Главные центральные оси. Эллипс инерции.
13
8.Поверочный расчет на ПЭВМ.
№ ВЕРШИНЫ |
Z – КООРДИНАТА |
1 |
12.5100 |
2 |
7.2000 |
3 |
7.2000 |
4 |
13.0000 |
5 |
13.0000 |
6 |
13.0000 |
7 |
0.0000 |
8 |
0.0000 |
9 |
7.2000 |
10 |
7.2000 |
11 |
12.5100 |
Y – КООРДИНАТА
0.8100
0.8100
0.0000
0.0000
14.0000
21.0000
21.0000
14.0000
14.0000
13.1900
1 3.1900
|
|
Yc |
i |
|
|
Y |
max |
min=3,4 |
|
|
|
|||
|
Zc |
C |
|
|
|
|
|
max=5,07 |
|
|
|
|
i |
|
|
|
|
|
|
Z |
min |
|
|
|
|
|
|
|
|
Рис. 5. Иллюстрация расчетов на ПЭВМ.
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ: ПЛОЩАДЬ 
СТАТИЧЕСКИЕ МОМЕНТЫ 
КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ЦЕНТРАЛЬНЫХ ОСЕЙ
ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
14
РАДИУСЫ ИНЕРЦИИ ТАНГЕНС УГЛА ДЛЯ
Способ расчета |
По п. п. 3.1-3.7 |
на ПЭВМ |
|
|
|
|
106,6 |
106.46 |
|
|
|
см |
15.96 |
15.98 |
|
|
|
см |
7.21 |
7.17 |
|
|
|
см4 |
1637.65 |
1618.77 |
|
|
|
см4 |
2330.79 |
2315.37 |
|
|
|
см4 |
675.38 |
-644.10 |
|
|
|
см4 |
2743.33 |
2699.34 |
|
|
|
см4 |
1225.11 |
1234.80 |
|
|
|
, град |
58.63 |
59.20 |
|
|
|
см |
5.07 |
5.04 |
|
|
|
см |
3.39 |
3.41 |
|
|
|
6. Пример 2. Фигура с вертикальной осью симметрии |
|||||||
|
|
Yс |
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
Yс1 |
0,48 |
|
|
|
|
0,73 |
|
|
|
|
|
|
|
Zс1 |
|
C1 |
|
|
|
|
6,40 |
Zс |
|
Yс2 |
|
1 |
3,20 |
||
Z |
o C |
|
|
|
|||
Zс2 |
|
C2 |
|
|
|
|
3,00 |
2 |
|
0,89 |
|
|
|||
|
|
|
|
||||
12,00 |
|
1,00 |
|||||
|
|
|
|
||||
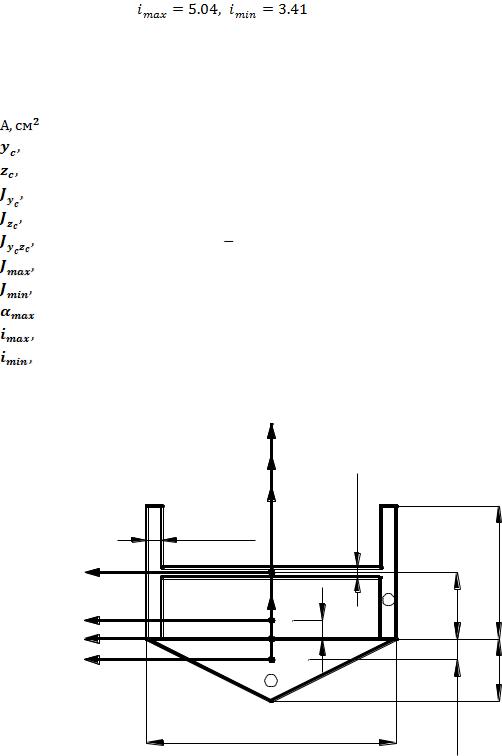
Рис. 6. Характерные размеры фигуры, см. |
|
||||||
1.На рис. 6 изображена в масштабе фигура, разобьём её на простейшие:
(1)- двутавр №12, по данным прил. 2: h=120мм, b=64мм, s=4.8мм, t=7.3мм, А1=14.7см2;
(2)- равнобедренный треугольник h2=3см, b2=12см.
15
2.На рис. 6 укажем расположения собственных центральных осей простей-
ших фигур. Площади простейших фигур: A1=14.7см2, А2=0.5
(h2
b2)=0.5
(3
12)=18cм2 с центрами тяжести в С1, C2 и центральными осями 
соответственно. Площадь всей фигуры A=A1+А2=14.7+18=32.7cм2.
Так как фигура имеет вертикальную ось симметрии, то для удобства расчетов совместим её с одной из осей системы координат ZOY (в нашем случае ось Y), а ось Z проведем по линии, разделяющей фигуры (1) и (2). Тогда:
С1: yc1= |
6.04 |
=3.20см; zc1=0; |
C2: yc2= |
1 |
|
h2 |
|
1 |
|
3 |
= -1.00 см; zc2 = 0. |
|
2 |
3 |
3 |
||||||||||
|
|
|
|
|
|
|
||||||
3. Определим положение центра тяжести всей фигуры и ее центральных осей. Для этого найдем сначала значения статических моментов
Sy= zc1 |
A1 |
+ zc2 |
A2 =0, |
|
|
|
|
Sz= yc1 |
A1 |
+ yc2 |
A2 =3.20 14.70+(-1.00) 18.00=47.04-18.00=29.04см3 |
|
|
||
Тогда |
|
yc = |
= 0.89см, |
zc = |
0 |
|
= 0. |
|
|
|
|||||
|
32.70 |
см2 |
|||||
По полученным данным на рис. 3 отметим точку С и проведем через нее центральные оси 
.
Вычислим в этих осях координаты точек С1 и С2 по формулам (10):
С1: |
y1 = 3.20 - 0.89 = 2.31см |
C2: |
|
y2 = -1.00 - 0.89 = -1.89 см |
|||||
|
z1 = 0 |
|
z2 = 0 |
|
|
||||
Выполним проверку 1 правильности расчетов: |
|
|
|||||||
Syc= |
A1+ A2 = 0 |
|
|
|
|
|
|
|
|
Szc= |
A1+ A2 = 2.31 14.70+(-1.89) 18.00= 33.96-34.02=-0.06 см3 |
||||||||
Погрешности допустимые, так как: |
|
|
|
= |
0.06 |
100% = 0.18% |
< 3%. |
||
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
34.02 |
|
|
|
4. Вычисляем осевые и центробежный моменты инерции каждой простейшей фигуры относительно собственных центральных осей.
|
для двутавра №12 по данным прил. 2: Jy = 27.90 cм4; Jz = 350 см4; |
С учетом принятой в расчетах системы координат, 
C
1
. (рис.6) отличающейся от табличной YCZ поворотом осей на 90 запишем:
Jyс1 = 350см4; Jzс1 = 27.9см4; а Jzc1yc1 = 0 в силу симметрии фигуры.
16
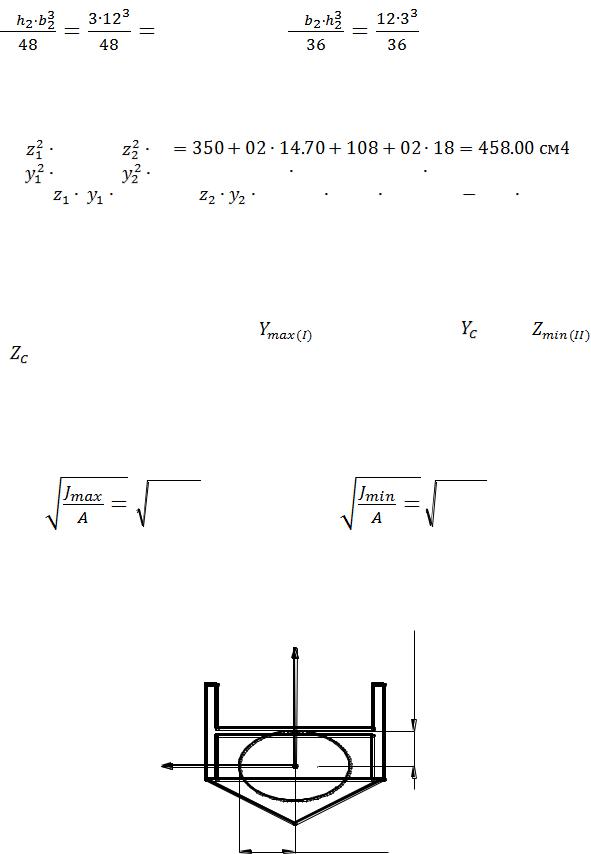
для фигуры (2) по формулам из прил. 1:
Jyc2 = |
108 см4; Jzc2 = |
= 9 см4; Jzc2yc2=0. |
5. Вычислим осевые и центробежный моменты инерции всей фигуры относительно найденных центральных осей 
, 
:
Jyc=Jyc1+ |
A1+Jyc2+ |
A2 |
|
Jzc=Jzc1+ |
A1+Jzc2+ |
A2=27.90+(2.31)2 14.70+9+(-1.89)2 18=179.64 см4 |
|
Jzcyc=Jzc1yc1+ |
A1+Jzc2yc2+ |
A2=0+0 (2.31) 14.70+0+( 1.89) 18=0 |
|
Система координат 
C
является главной центральной, т.к. проходит через центр тяжести и центробежный момент инерции равен 0.
6.Найдем главные моменты инерции. Как следует из п.5:
Jmax = 458.00 см4, |
Jmin = 179.64 см4. |
|
При этом, как показано на рис.7, ось |
совпадает с осью , а ось |
с |
осью . Таким образом, max = 0. |
|
|
Проверка 2 в этом случае выполняется тождественно.
7.Построим главный центральный эллипс инерции в найденных осях. Для этого вычислим главные центральные радиусы инерции:
|
|
|
|
|
|
|
imax= |
458.00 |
= 3.74см; imin= |
179.64 |
= 2.34см |
||
32.70 |
|
32.70 |
||||
|
|
|
||||
На рис. 7 изобразим заданную фигуру, главные центральные оси и главный центральный эллипс инерции, откладывая imax от оси 
, а imin- от оси
.
Yc (Imax) |
min=2,34i |
Zc (Imin) |
C |
i max=3,74 |
Рис. 7. Главные центральные оси. Эллипс инерции
17
8. Поверочный расчет на ПЭВМ. |
||||
|
|
Y |
|
|
4 |
5 |
|
8 |
9 |
|
6 |
|
7 |
|
Z |
13 |
|
12 |
|
|
C |
|
|
|
|
14 |
11 |
|
|
3 |
|
1, 10 |
||
|
|
|
||
|
|
2 |
|
|
|
|
Ymax |
|
|
4 |
5 |
|
8 |
9 |
|
6 |
|
7 |
|
Zmin |
13 |
|
12 |
|
|
C |
|
|
|
|
14 |
11 |
|
|
3 |
|
1, 10 |
||
|
|
|
2
Рис. 8. Иллюстрация расчетов на ПЭВМ
№ ВЕРШИНЫ |
Z – КООРДИНАТА |
Y – КООРДИНАТА |
1 |
-6.0000 |
0.0000 |
2 |
0.0000 |
-3.0000 |
3 |
6.0000 |
0.0000 |
4 |
6.0000 |
6.4000 |
5 |
5.2700 |
6.4000 |
6 |
5.2700 |
3.4400 |
7 |
-5.2700 |
3.4400 |
8 |
-5.2700 |
6.4000 |
9 |
-6.0000 |
6.4000 |
10 |
-6.0000 |
0.0000 |
11 |
-5.2700 |
0.0000 |
12 |
-5.2700 |
2.9600 |
13 |
5.2700 |
2.9600 |
14 |
5.2700 |
0.0000 |
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ: ПЛОЩАДЬ 
СТАТИЧЕСКИЕ МОМЕНТЫ 
КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ 
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ЦЕНТРАЛЬНЫХ ОСЕЙ
ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ 
РАДИУСЫ ИНЕРЦИИ 
ТАНГЕНС УГЛА ДЛЯ 
УГОЛ В ГРАДУСАХ
18
Способ расчета |
По п. п. 3.1-3.7 |
на ПЭВМ |
|
|
|
|
32.70 |
32.40 |
|
|
|
см |
0.89 |
0.87 |
|
|
|
см |
0 |
0.00 |
|
|
|
см4 |
458.00 |
451.95 |
|
|
|
см4 |
179.64 |
182.13 |
|
|
|
см4 |
0 |
0.00 |
|
|
|
см4 |
458.00 |
451.95 |
|
|
|
см4 |
179.64 |
182.13 |
|
|
|
, град |
0 |
0 |
|
|
|
см |
3.74 |
3.73 |
|
|
|
см |
2.34 |
2.37 |
|
|
|
7. Пример 3. Фигура с горизонтальной осью симметрии
Рис. 9. Характерные размеры фигуры, см.
1. На рис. 9 изображена в масштабе фигура, разобьём её на простейшие:
(3)- двутавр №10, по данным прил. 2: h=100мм; b=55мм; s=4.5мм; t=7.2мм;
А1=12см2.
(4)- полукруг r=5см.
2.На рис. 6 укажем расположения собственных центральных осей простей-
ших |
фигур. |
Площади |
простейших |
фигур: |
A1=12см2; |
19
|
r2 |
|
3.14 52 |
=39.25cм2, с центрами тяжести в С1, C2 |
|
|
А2= |
2 |
= |
|
|
и центральными |
|
|
2 |
|||||
|
|
|
|
|
||
осями |
Yc1, |
Zc1; Yc2, Zc2 соответственно. Площадь |
всей фигуры |
|||
A=A1+А2=12+39.25=51.25cм2.
Так как фигура имеет горизонтальную ось симметрии, то для удобства расчетов совместим её с одной из осей (в нашем случае ось Z) системы координат ZOY. Ось Y проведем по линии, разделяющей фигуры (1) и (2).
Тогда: |
|
|
|
|
|
|
С1: yc1 = 0; zc1 = 5см; |
C2: yc2 = 0; zc2 = |
4 r |
|
4 5 |
2.12см |
|
3 |
3 3.14 |
|||||
|
|
|
|
3. Определим положение центра тяжести всей фигуры и ее центральных осей. Для этого найдем сначала значения статических моментов
Sz= yc1 |
A1 |
+ yc2 |
A2 =0 12.00+0 |
39.25=0 |
39.25=60.00-83.21=-23.21см3. |
||
Sy= zc1 |
A1 |
+ zc2 |
A2 =5.00 12.00+(-2.12) |
||||
|
|
|
0 |
|
|
23.21 см3 |
|
Тогда |
yc = |
|
|
= 0 |
zc = |
51.25 см2 =-0.45 см. |
|
|
51.25 см2 |
||||||
По полученным данным на рис. 9 отметим точку С и проведем через нее цен-
тральные оси |
, . |
|
|
|
|
|
|
|
|
Вычислим в этих осях координаты точек С1 и С2 по формулам (10): |
|
||||||||
С1: |
y1 = 0 |
|
C2: y2 = 0 |
|
|||||
|
z1 = 5 - (-0.45) = 5.45 см |
|
|
|
z2 = -2.12 - (-0.45) = -1.67 см |
||||
Выполним проверку 1 правильности расчетов: |
|
||||||||
Syc= |
A1+ |
A2 = 5.45 12+(-1.67) 39.25=65.46-65.47 = -0.01 см3 |
|
||||||
Szc= |
A1+ |
A2 = 0 |
|
|
|
|
|
|
|
Погрешности допустимые, так как: |
|
|
|
= |
0.01 |
100% = 0.02% |
< 3% |
||
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
65.46 |
|
|
|
4. Вычисляем осевые и центробежный моменты инерции каждой простейшей фигуры относительно собственных центральных осей.
для двутавра №10 по данным прил. 2: Jy=17.90 см4; Jz=198 cм4;
|
|
r4 |
3.14 54 |
||
|
для фигуры (2) по формулам из прил. 1: Jyc = |
|
|
245.31 см4 |
|
8 |
|||||
|
|
8 |
|
||
Jzc = 0.11 r4 0.11 54 68.75 см4; Jyczc= 0.
20