12.3. Обобщённая характеристика триггеров

Триггер – это устройство, которое может находиться в одном из двух устойчивых состояний и переходить из одного состояния в другое под воздействием входных сигналов. Триггеры – это элементарные автоматы с памятью, которые являются основой для построения сколь угодно сложных автоматов с памятью. Входы триггеров условно подразделяют на информационные и управляющие.

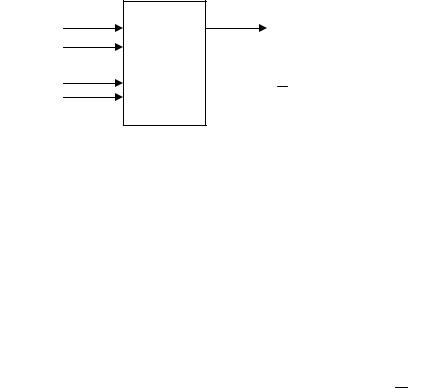
На уровне чёрного ящика триггер можно представить так, как на рис. 12.4.

Рис. 12.4. Представление триггера на уровне черного ящика

где Инф. – информационные входы; Упр. – управляющие входы триггера.

Следует отметить, что на практике часты ситуации, когда информационные входы одновременно являются управляющими, а управляющие - одновременно информационными.

Условились считать, что внутреннее состояние триггера однозначно связано с его выходным сигналом Q (прямой выход). Если на прямом выходе сигнал единичный, то говорят: триггер находится в единице (единичном состоянии). Если на прямом выходе сигнал нулевой, то говорят, что триггер нахо-

дится в нуле (нулевом состоянии). При этом, если Q =1, то Q = 0 и наоборот.

152