Учебное пособие 1518

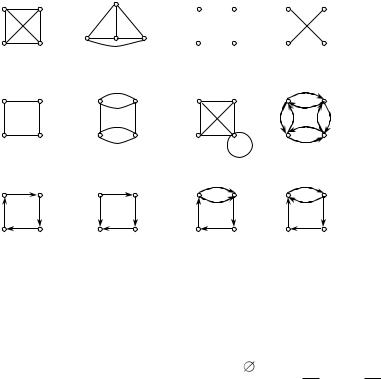
Пример 3.2.

Сравнить графы:

Рис. 2

1.G1- G7 – н-графы; G8 - G12 - орграфы.

2.G1, G2 – полные, причем G1= G2.

3.G7 – не является полным, т.к. есть петля

4. G3 – граф с пустым множеством ребер (Е= ).

5.G4 и G5 – является дополнением друг к другу, G4 = G5 ; G5 = G4

6.G6– мультиграф т.к. содержит кратные ребра

7.G8 – орграф, канонически соответствует G5.

8.G9, G10 не равны.

9.G11 – ориентированный мультиграф; G12 мультиграфом не являет-

ся.

3.2. Способы задания графов

Мы уже рассмотрели графический способ задания графа. Рассмотрим другие способы задания. В общем виде задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности.

31

Для описания вершин и ребер достаточно их занумеровать. Пусть v1, v2,…, vn - вершины графа G; e1,…, em – его ребра. Отношение инцидентности задается:

1)Матрицей инцидентности ( i,j) размера n m: по вертикали

игоризонтали указываются вершины и ребра соответственно, а на пересечении i-й вершины и j-го ребра в случае н-графа ставят 1, если они инцидентны и 0 – если нет.

В случае орграфа : -1, если вершина является началом ребра, 1

– если концом и 0 если вершина и ребро не инцидентны; если некоторая вершина является для ребра началом и концом (петля), проставляется 2.

2)Списком ребер графа. Два столбца: в левом перечисляются

все ребра ei E и в правом – инцидентные ему вершины; для н-графа в произвольном порядке, а для орграфа сначала начало, потом конец.

3) Матрица смежности ( ке) – квадратная матрица размера n n: по вертикали и горизонтали перечисляются все вершины vi V а на пересечении к-й и l-й вершин в случае н-графа проставляется число, равное числу ребер с началом в к-й вершине и концом в l-й.

Если два графа равны, то их матрицы совпадают. Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована.

Изоморфные графы (т.е. отличающиеся только нумерацией вершин) имеют разные матрицы инцидентности и смежности и списки ребер. Проверка изоморфности графов является трудоемкой задачей.

Пример 3.3.: Написать списки ребер, матрицы инцидентности и смежности для следующих графов:

Рис. 3

32

Список ребер один и тот же (но для G1 порядок вершин безразличен)

33

При наличии матрицы инцидентности число всех вершин и ребер графа определяется естественным образом по размеру матрицы. То же с определением числа ребер по списку ребер; число вершин равно максимальному номеру из перечисленных номеров вершин.

Матрица смежности н-графа симметрична относительно главной диагонали и все его ребра определяются правым верхним треугольником, расположенным над диагональю, включая и ее.

Число ребер. Для орграфа ребра определяются всей матри-

n

3.3. Операции над частями графа

Граф Н называется частью графа G, H G, если множества его вершин и ребер V(H) и E(H) содержатся соответственно в V(G) и E(G). Если V(G) = E(G), то часть H графа G называется суграфом.

Суграф Н является перекрывающим для н-графа G, если любая вершина графа G инцидентна хотя бы одному ребру из H.

Подграфом G(V ) графа G(V) с множеством вершин V V называется часть, которой принадлежат все ребра с обоими концами из H.

Над частями графа G производятся следующие операции:

1.Дополнение H к части H определяется множеством всех ребер G, не принадлежащих Н:

34

если любая вершина графа G инцидентна не более, чем двум его ребрам.

Контур – путь, в котором v0 = vn. Контур называется циклом, если он является цепью, и простым циклом, если это простая цепь. Если граф содержит циклы, то он содержит и простые циклы: граф без циклов называется ациклическим.

Вершина v G называется достижимой из вершины v G если имеется путь L(v ,…,v ) с началом vи концом v .

Орграф называется связным если он связан без учета ориентации дуг, и сильно связным, если из любой вершины vв любую вершину v существует путь. Число ребер пути называется его длиной.

Расстоянием (v’,v ) между вершинами vи vн-графа G на-

зывается минимальная длина простой цепи с началом v и концом v . Центром называется вершина н-графа, от которой максимальное расстояние до других вершин являлось бы минимальным. Мак-

симальное расстояние от центра G до его вершин называется ра-

диусом графа r(G).

Эйлеров цикл – цикл графа, содержащий все ребра графа. Эйлеров граф – граф, имеющий эйлеров цикл (эйлеров цикл

можно считать следом карандаша, вычерчивающего этот граф без отрыва от бумаги).

Имеет место теорема Эйлера: конечный неориентированный граф G – эйлеров тогда и только тогда, когда он связан и степени всех его вершин четны.

Эйлерова цепь – цепь, включающая все ребра данного конечного н-графа G, но имеющая различные начало v' и конец v . Чтобы в конечном н-графе G существовал эйлеров цикл, необходимы и достаточны его связанность и четность степеней всех вершин, кроме начальной v' и конечной v(они должны иметь нечетные степени). Чтобы в конечном орграфе существовал эйлеров цикл, необходима и достаточна его связность, а также равенство степеней вершин этого графа по входящим и выходящим ребрам, т.е. 1(V) = 2(V),

V G.

Гамильтонов цикл – простой цикл, проходящий через все вершины рассматриваемого графа. Гамильтонова цепь – простая цепь, проходящая через все вершины графа с началом и концом в разных точках.

36

где Vc - число связанных компонент графа; Ve - число его ребер; VV - число вершин. V(G) для любого конечного н-графа неотрицательно. Цикломатическое число любого дерева и леса равно нулю. Действительно Vc- Vе =1, а число связанных компонент дерева Vc=1.

E5=(2,5,6,7).

тогда M={Eo; E1; E2, E3, E4, E5} будет сетью.

Если множество М и набор N конечны, сеть называется

конечной.

Сеть, в которой бесконечно хотя бы М или N называется бесконечной. Частным случаем бесконечных сетей являются счетные сети, т.е. те, у которых М и N не более чем счетны.

Для любой счетной сети определена ее геометрическая реализация. Например, для рассмотренной сети:

38

4.Введение в теорию алгоритмов

4.1.Предварительные обсуждения

Салгоритмами, т.е. эффективными процедурами, однозначно приводящими к результату, мы уже сталкивались. Школьные методы умножения столбиком, деления углом, правило дифференцирования сложной функции и т.д. – все это алгоритмы.

Каковы должны быть требования к алгоритму?

1. Любой алгоритм имеет дело с исходными данными и выдает результат. В технических терминах это означает, что алгоритм имеет входы и выходы. Кроме того, в ходе работы алгоритма получаются и промежуточные результаты, используемые в дальнейшем. Таким образом любой алгоритм имеет дело с данными – входными, выходными и промежуточные результаты. Какие объекты можно считать

данными?

Ясно, что объекты должны быть четко определены и отличны друг от друга, а также от „„не объектов”. К таким алгоритмическим объектам относятся числа, векторы, матрицы смежности графов, формулы и т.д. Такие объекты, как „„рисунок”, „„хорошая книга”, „„осмысленное утверждение”, с которыми работает человек, алгоритм воспринимать не будет.

В теории алгоритмов фиксируют конкретные конечные наборы исходных объектов, называемых элементарными (цифры, буквы

ит.д.), которые образуют алфавит. Из алфавита строятся другие объекты. Типичным средством построения являются индуктивные определения, указывающие как строить новые объекты из уже построенных.

Простейшее индуктивное определение – это определение некоторого множества слов, классическим примером которого служит определение идентификатора:

Идентификатор – это либо буква, либо идентификатор к которому приписана справа буква или цифра. Слова конечной длины в конечных алфавитах (в частности, числа) – наиболее обычный тип алгоритмических данных, а число символов в слове (длина слова) – естественная единица измерения объема обрабатываемой информации. Более сложный случай алгоритмических объектов – формулы. Они определяются индуктивно и так же являются словами в конечном алфавите, однако не каждое слово является формулой. В этом

40