
Учебное пособие 1395
.pdf3x1 2x2 4x3 21, 1.2. 3x1 4x2 2x3 9,
2x1 x2 x3 10.
Решить систему линейных уравнений с помощью метода Гаусса с выбором главного элемента:
x1 6.25x2 0.5x3 7.5, 1.3. 5x1 x2 2.12x3 8.68,
2.12x1 0.5x2 3.6x3 0.24.
Вычислить определитель матрицы с помощью метода Гаусса:
|
|
5 |
4.5 8 |
|
||
1.4. |
|
|
|
4.1 |
|
|
2.8 3 |
. |
|||||
|
|
2.4 |
4 |
5.6 |
|
|
|
|
|
||||
|
2 |
3 |
1 |
|
|
|
1.5. |
|
|
1 |
4 |
|
|
2 |
. |
|
||||
|
|
6 |
5 |
2 |
|
|
|
|
|
|
|||
Найти обратную матрицу с помощью метода Гаусса:
|
2 |
3 |
1 |
|
|
1.6. |
|
6 |
2 |
|
|
1 |
. |
|
|||
|
|
2 |
1 |
|
|
|
1 |
|
|
||
Решить систему линейных уравнений методом |
|||||
прогонки: |
2x1 x2 |
5, |
|||
|
|||||
|
|
10x2 5x3 |
18, |
||
1.7. |
x1 |
||||
|
|
x2 5x3 2x4 |
40, |
||
|
|
|
|||
|
|
|
|
x3 4x4 |
27. |
|
|
|
|
||
31
|
5x1 x2 |
|
2, |
|
|
|
4.6x2 |
x3 |
3.3, |
1.8. |
2x1 |
|||
|
2x2 |
3.6x3 0.8x4 |
2.6, |
|
|
|
|||
|
|
|
3x3 4.4x4 |
7.2. |
|
|
|
||
Решить систему линейных уравнений методом квадратных корней:
x1 2x2 x3 2x4 15,
1.9. 2x1 5x2 3x3 x4 18,x1 3x2 11x3 3x4 12,
2x1 x2 3x3 30x4 93.
x1 0.422x2 0.54x3 0.66x4 |
0.3, |
|||||||||
0.42x |
|
|
x |
|
0.32x |
|
0.44x |
|
0.5, |
|
1.10. |
1 |
|
|
2 |
|
|
3 |
|
4 |
|
0.54x1 |
|
0.32x2 |
x3 |
0.22x4 |
0.7, |
|||||
|
|
|
0.44x2 |
0.22x3 x4 |
0.9. |
|||||
0.66x1 |
||||||||||
Решить систему линейных уравнений методом простой итерации с точностью 0.01:
|
100x1 |
6x2 |
2x3 |
200, |
||
1.11. |
|
6x1 200x2 |
10x3 |
600, |
||
|
|
x1 |
2x2 |
100x3 500. |
||
|
|
|||||
|
20x1 3x2 |
2x3 |
40, |
|||
1.12. |
|
4x1 30x2 |
x3 |
20, |
||
|
|
x1 |
2x2 20x3 |
30. |
||
|
|
|||||
Решить систему линейных уравнений методом ГауссаЗейделя с точностью 0.01:
20x1 |
|
2x2 |
2x3 |
10, |
||
1.13. |
2x1 |
|
10x |
2 |
x3 |
16, |
|
2x1 5x |
2 |
6x3 |
30. |
||
|
||||||
32
10x1 3x2 2x3 30,
1.14. |
5x1 30x2 |
x3 |
20, |
|
x1 x2 |
6x3 |
18. |
|
33
2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
2.1. Основные этапы поиска корней нелинейного уравнения
Задача нахождения корней нелинейного уравнения вида
F(x) 0
встречается в различных областях научной или прикладной деятельности. Как и в случае линейных уравнений, методы их решения делятся на две группы:
-прямые;
-итерационные.
Прямые методы позволяют записать для корней некоторые конечные формулы. Но, как правило, они предназначены для решения простых уравнений определенного вида (квадратных, логарифмических, тригонометрических и т.д.).
Итерационные методы являются более универсальными и позволяют решать сложные практические задачи. Алгоритм поиска корней уравнения с помощью итерационных методов состоит из двух этапов:
1)локализация решения – на этом этапе производится определение отрезка, содержащего корень уравнения; такой отрезок может находиться из физических соображений, с помощью графических или других методов; для некоторых методов достаточно задание не отрезка, а одной точки – начального приближения;
2)итерационное уточнение начального приближения до требуемой степени точности.
2.2. Метод половинного деления
Пусть на этапе локализации решения было установлено, что искомое значение корня уравнения x c расположено на
34

отрезке a,b . Тогда в качестве начального приближения c0 принимается середина отрезка c0 (a b)/2. Далее значение функции F(x) исследуется на концах отрезков [a,c0] и [c0,b]. Тот из отрезков, на концах которого F(x) принимает значения различных знаков, содержит искомый корень; поэтому он принимается в качестве нового отрезка [a1,b1]. Вторая половина отрезка a,b , на которой знак F(x) не меняется, отбрасывается. В качестве первого приближения корня принимается середина нового отрезка c1 (a1 b1)/2 и т. д. Таким образом, k-е приближение вычисляется как
ck ak bk . 2
Процесс решения продолжается до тех пор, пока не будет выполнено условие
|
|
bk ak , |
|
|
|
|
где - необходимая точность решения. |
|
|
||||
Пример. Найти корень |
уравнения x2 3x 4 0 на |
|||||
отрезке |
[0, 1.5] |
точностью |
0.01 |
с |
помощью |
метода |
половинного деления. |
|
|
|
|
||
Проверим |
наличие корня |
на |
заданном |
отрезке: |
||
F(0) 4, |
F(1.5) 2.75. Поскольку значения функции на концах |
|||||
отрезках имеют разные знаки, то отрезок содержит корень уравнения.
Положим а0 0, b0 1.5, c0 |
(a0 |
b0)/2 |
0.75. |
|||
1 |
итерация: F(c0) 1.188. Т.к. F(c0) F(b0) |
0, то далее |
||||
будем |
рассматривать |
отрезок [a1,b1] [0.75, 1.5]. Вычислим |
||||
c1 (a1 |
b1)/2 1.125. |
|
|
|
|
|
2 |
итерация: |
F(c1) 0.641. |
Т.к. |
F(a1) F(c1) 0, то |
||
[a2,b2] [0.75, 1.125], c2 (a2 b2)/2 0.9375.
Результаты следующих итераций приведены в табл. 5. Как видно из таблицы, заданная точность достигнута
при n 8 и можно принять x с8 0.999. Если бы нужно было
35
найти более точное решение, то уже на следующей итерации мы бы получили, что x 1.
|
|
|
|
|
Таблица 5 |
|
|
|
|
|
|
|
|
Номер |
an |
bn |
сn |
F(сn ) |
|
|
итерации |
bn an |
|
||||
n |
|
|
|
|
|
|
0 |
0 |
1.5 |
0.75 |
-1.188 |
1.5 |
|
1 |
0.75 |
1.5 |
1.125 |
0.641 |
0.75 |
|
2 |
0.75 |
1.125 |
0.9375 |
-0.309 |
0.375 |
|
3 |
0.9375 |
1.125 |
1.031 |
0.157 |
0.188 |
|
4 |
0.9375 |
1.031 |
0.984 |
-0.078 |
0.094 |
|
5 |
0.984 |
1.031 |
1.008 |
0.039 |
0.047 |
|
6 |
0.984 |
1.008 |
0.996 |
-0.02 |
0.024 |
|
7 |
0.996 |
1.008 |
1.002 |
0.01 |
0.012 |
|
8 |
0.996 |
1.002 |
0.999 |
-0.005 |
0.006 |
|
2.3. Метод хорд
В методе хорд процесс итераций состоит в том, что в
качестве приближений |
к корню |
уравнения |
F(x) 0 |
принимаются значения |
c0,c1,... точек |
пересечения |
хорды с |
осью абсцисс.
Сначала находим уравнение хорды, проходящей через точки a и b:
y F(a) |
|
x a |
. |
F(b) F(a) |
|
||
|
b a |
||
Для точки пересечения ее с осью абсцисс (x c0,y 0) получим уравнение
c0 a |
b a |
F(a). |
|
||
|
F(b) F(a) |
|
Далее, сравнивая знаки величин F(a) и F(c0), находим ту половину отрезка, на концах которого знаки функций противоположны. Следующая итерация состоит в определении
36
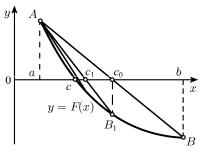
нового приближения с1 как точки пересечения хорды с осью абсцисс и т. д. (рис. 1).
Рис. 1. Решение нелинейного уравнения с помощью метода хорд
Условием окончания в методе хорд служит условие близости двух последовательных приближений
ck ck 1 |
. |
По сравнению с методом половинного деления метод хорд обладает более высокой скоростью сходимости, т.е. позволяет найти решение уравнения за меньшее число итераций. Кроме того, оба рассмотренных метода не требуют
знания дополнительной информации о |
функции F(x). |
||||
дифференцируема. |
|
|
|
x2 3x 4 0 на |
|
Пример. Найти |
корень уравнения |
||||
отрезке [0, 1.5] точностью 0.01 с помощью метода хорд. |
|||||
Определим точку пересечения хорды с осью абсцисс: |
|||||
c0 0 |
1.5 0 |
|
( 4) 0.8889. |
||
2.75 ( 4) |
|||||
|
|
|
|||
Найдем значение функции |
F(c0) 0.5427. Поскольку |
||||
F(b) F(c0) 0, то a c0 . Вычислим следующее приближение:
c 0.8889 |
1.5 0.8889 |
( 0.5427) 0.9897 |
|
||
1 |
2.75 ( 0.5427) |
|
|
|
и т.д. Результаты занесем в табл. 6.
37
Таблица 6
Номер |
сn |
|
итерации |
сn сn 1 |
|
n |
|
|
0 |
0.8889 |
- |
1 |
0.9897 |
0.1008 |
2 |
0.9991 |
0.0094 |
Как видно из результатов вычислений, решение с требуемой точностью получено уже на второй итерации.
2.4. Метод Ньютона (метод касательных)
В отличие от предыдущих двух методов, не требующих знания о дифференцируемости функции F(x), метод Ньютона является более сложным алгоритмом, использующим в итерационном процессе производную исходной функции. Как результат, метод обладает более быстрой сходимостью (для некоторых видов функций), но в то же время применяется для решения более узкого класса задач и его сходимость не всегда гарантирована.
Отличие метода Ньютона от метода хорд состоит в том, что на k-й итерации вместо хорды проводится касательная к кривой y F(x) при x ck 1 и находится точка пересечения касательной с осью абсцисс. При этом не обязательно задавать отрезок [a,b], содержащий корень уравнения, а достаточно лишь найти некоторое начальное приближение корня x c0
(рис. 2).
38
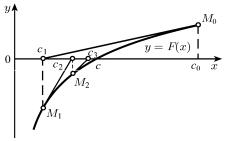
Рис. 2. Решение нелинейного уравнения с помощью метода Ньютона
Уравнение касательной, проведенной к кривой y F(x) в точке с координатами c0 и F(c0), имеет вид
y F(c0) F (c0)(x c0).
Отсюда найдем следующее приближение корня c1 как абсциссу точки пересечения касательной с осью x (y 0):
c1 c0 F(c0)/F (c0) .
Аналогично могут быть найдены и следующие приближения
ck ck 1 F(ck 1)/F (ck 1), |
k 1,2,... |
Условием окончания работы метода Ньютона также может служить условие близости двух последовательных приближений.
Несмотря на то, что на каждой итерации объем вычислений в данном методе больший, чем в методах половинного деления и хорд, поскольку приходится находить значение не только функции F(x) , но и ее производной, скорость сходимости здесь значительно выше, чем в других методах.
Пример. |
Найти корень |
уравнения |
x2 3x 4 0 на |
отрезке [0,1.5] |
точностью |
0.01 с |
помощью метода |
касательных. |
|
|
|
39
Найдем производную заданной функции:
F(x) 2x 3.
В качестве начального значения возьмем точку c0 0 и
определим первое приближение:
c1 0 ( 4)/3 1.3334.
Результаты вычисления остальных приближений занесем в табл. 7.
Таблица 7
Номер |
сn |
|
итерации |
сn сn 1 |
|
n |
|
|
0 |
0 |
- |
1 |
1.3334 |
1.3334 |
2 |
1.097 |
0,2364 |
3 |
1 |
0.097 |
4 |
1 |
0 |
Как видно из результатов вычислений, решение с заданной степенью точности получено на четвертой итерации.
Контрольные вопросы
1.Какие группы методов существуют для решения нелинейных уравнений?
2.Из каких основных этапов состоит процесс решения нелинейного уравнения с помощью итерационных методов?
3.Как найти корень нелинейного уравнения с помощью метода половинного деления?
4.В чем заключается метод хорд решения нелинейных уравнений?
5.Как найти корень нелинейного уравнения с помощью метода Ньютона? Чем данный метод отличается от метода половинного деления и метода хорд?
40
