Метрология. методические указания к практическим занятиям для студентов направления 13.03.01 «Теплоэнергетика и теплотехника». Надеев А.А

345-221

МЕТРОЛОГИЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практическим занятиям

для студентов направления 13.03.01 «Теплоэнергетика и теплотехника» (профиль «Промышленная теплоэнергетика») всех форм обучения

Воронеж 2021

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

Кафедра теоретической и промышленной теплоэнергетики

МЕТРОЛОГИЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практическим занятиям

для студентов направления 13.03.01 «Теплоэнергетика и теплотехника» (профиль «Промышленная теплоэнергетика») всех форм обучения

Воронеж 2021

ВВЕДЕНИЕ

Практические задания по дисциплине «Метрология» предназначены для закрепления обучающимися теоретического материала и получения ими практических навыков по обработке результатов измерений, оценки погрешностей измерений (средств измерений), овладения основными методами измерений электрических и неэлектрических величин на объектах теплоэнергетики и теплотехники.

В начале каждого раздела методических указаний приведены краткие теоретические сведения по изучаемому вопросу.

Практические задания предназначены для студентов, обучающихся по направлению 13.03.01 «Теплоэнергетика и теплотехника», профиль «Промышленная теплоэнергетика». Умения и навыки, полученные при выполнении данных заданий, необходимы при освоении дисциплины «Теплотехнические измерения и автоматизация».

3

1. ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

1.1.Краткие теоретические сведения

Качество всех средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия «погрешность» требует определения и чёткого разграничения трёх понятий: истинного и действительного значений измеряемой физической величины и результата измерения.

Истинное значение физической величины xи – это значение, идеальным

образом отражающее свойство данного объекта, как в количественном, так и в качественном отношении.

Истинное значение априори считается неизвестным и применяется только в теоретических исследованиях. В редких случаях за истинное значение принимается значение, определённое с применением первичных или вторичных эталонов. По этой причине оно заменяется понятием «действительное значение».

Действительное значение физической величины xд – это значение,

найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Действительное значение может быть определено при помощи рабочих эталонов.

Результат измерения (измеренное значение) физической величины x – это приближённая оценка истинного значения величины, найденная путём измерения (результат, полученный с помощью рабочего средства измерения).

Различают понятия «погрешность результата измерения» и «погрешность средства измерения».

Погрешность результата измерения – это отклонение результата измерения от истинного значения измеряемой величины.

Погрешность средства измерения – это отклонение показания средства измерения от истинного (действительного) значения измеряемой величины. Оно характеризует точность результатов измерений, проводимых данным средством.

Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам.

По способу выражения различают абсолютные, относительные и приведённые погрешности.

Абсолютная погрешность х – это разность между измеренным и истинным (действительным) значениями измеряемой величины, выраженная в тех же единицах, что и измеряемая величина:

Абсолютная погрешность не может в полной мере служить показателем точности измерений, поэтому введено понятие «относительная погрешность».

4

Относительная погрешность х – это отношение абсолютной погрешности измерения к истинному (действительному, измеренному) значению величины, выраженное в процентах:

Нормирующее значение постоянно во всём диапазоне измерений или его части. Оно определяется по формуле

где xmax , xmin – максимальное и минимальное значение диапазона из-

мерения прибора.

Таким образом, нормирующее значение представляет собой ширину диапазона измерения прибора.

Приведённая погрешность считается основной метрологической характеристикой измерительного прибора.

Одним из параметров, характеризующих точность средства измерений (измерительного прибора), является класс точности, характеризующий величину погрешности при измерении физической величины.

Класс точности – это обобщённая характеристика средства измерений, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность.

Класс точности не является непосредственной оценкой точности измерений, выполняемых этим средством измерений, поскольку погрешность зависит ещё от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится

5

погрешность средства измерений данного типа. Он обычно указывается на шкале или корпусе прибора.

Наиболее часто применяются следующие три способа задания классов точности измерительного прибора:

- 1-й способ – класс точности задаётся в виде числа K . При этом нормируется основная приведённая погрешность x прибора, выраженная в процентах, которая во всех точках шкалы не должна превышать по модулю числа K ,

т.е. x K , %;

- 2-й способ – класс точности задаётся в виде числа K в кружочке K . При этом нормируется основная относительная погрешность, выраженная в процентах, т.е. x K , %;

- 3-й способ – класс точности задаётся двумя числами, разделёнными косой чертой a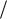b , причём a b . При этом нормируется основная относительная

b– за мультипликативную составляющую погрешности.

1.2.Практические задания

1.1.Вольтметр имеет шкалу от 0 до 100 В и абсолютную погрешностьU = 1 В. Им измерены следующие значения напряжения: 0; 10; 20; 40;

50; 60; 80; 100 В. Определить зависимости абсолютной, относительной и

6

Окончание таблицы 1.1

50

60

80

100

1.2. Амперметр имеет шкалу от 0 до 50 А и относительную погрешность I = 2 %. Им измерены следующие значения силы тока: 0; 5; 10; 20; 25; 30; 40; 50 А. Определить зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

1.3. Омметр имеет шкалу от 0 до 20 кОм. Им измерены значения сопротивления: 0; 1; 4; 5; 10; 12; 17; 20 кОм. Определить значения абсолютной и относительной погрешностей, если приведённая погрешность R равна 1%. Результаты представить в виде таблицы и графиков.

1.4.Термометр имеет шкалу от минус 50 до 70 °С и абсолютную погрешность T = 1 °С. Им измерены следующие значения температуры: -50; -40; -20; -10; 0; 10; 20; 50; 70 °С. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

1.5.Газоанализатор имеет шкалу от 0 до 10 %. Им измерены следующие значения концентрации диоксида углерода: 0; 1; 3; 5; 7; 9; 10 %.

Определить значения абсолютной и приведённой погрешностей, если относительная погрешность СCO2 равна 5 %. Результаты представить в виде

таблицы и графиков.

1.6.Кислородомер имеет шкалу от 2 до 21 %. Им измерены следующие значения концентрации кислорода: 2; 5; 10; 13; 17; 20; 21 %. Опред е- лить значения абсолютной и относительной погрешностей, если приведённая погрешность равна 2 %. Результаты представить в виде таблицы и графиков.

1.7.Уровнемером со шкалой от 1 до 20 м, имеющим приведённую

погрешность H = 1 %, измерены значения уровня: 1; 6; 8; 10; 14; 16; 18; 20 м. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

1.8.Расходомером со шкалой от 0 до 50 м3/ч, имеющим абсолютную погрешность V = 1 м3/ч, измерены значения расхода: 0; 5; 10; 15; 20; 25; 30; 40; 50 м3/ч. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить

ввиде таблицы и графиков.

1.9.Манометром со шкалой от 0 до 0,25 МПа измерены значения из-

быточного давления: 0; 0,02; 0,06; 0,08; 0,1; 0,15; 0,2; 0,25 МПа. Опреде-

7

лить значения абсолютной и относительной погрешностей, если приведённая погрешность манометра равна 1,5 %. Результаты представить в виде таблицы и графиков.

1.10.Амперметром со шкалой от 0 до 50 А, имеющим класс точности 2.0, измерены следующие значения силы тока: 0; 5; 10; 20; 25; 30; 40; 50 А. Определить зависимости абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

1.11.Вольтметром со шкалой от 0 до 100 В, имеющим класс точности 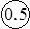, измерены следующие значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 В. Определить зависимости абсолютной и относительной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

1.12.Цифровым омметром, имеющим класс точности 1.0/0.5 со шкалой от 0 до 1000 Ом, измерены следующие значения сопротивления: 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Определить зависимости абсолютной и относительной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

8

2. ГРУБЫЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

2.1. Краткие теоретические сведения

По характеру проявления все погрешности измерений подразделяются на случайные, систематические и грубые (промахи).

Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности могут быть предсказаны, обнаружены и, благодаря этому, почти полностью устранены введением соответствующей поправки или регулировкой средства измерения.

Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии многократных равноточных измерений одного и того же значения физической величины.

Появление случайных погрешностей не подчиняется какой-либо закономерности. Они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения.

Грубая погрешность (промах) – это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Грубые погрешности, как правило, возникают из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчёта, считывания, ошибок в записях или вычислениях и др.) и кратковременных резких изменений условий проведения эксперимента. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают. Однако чаще всего промахи выявляют только при окончательной обработке результатов измерений с помощью специальных статистических критериев.

Одним из критериев для оценки наличия или отсутствия грубой погрешности является критерий Романовского, применяемый, как правило, при объёмах выборки не более 20.

В данном случае используется уровень значимости , вычисляемый по формулам:

где M x – математическое ожидание (среднее арифметическое);

9