Методические указания к выполнению контрольных работ по дисциплине «Физические основы обработки материалов резанием». Жачкин С.Ю., Симонова Ю.Э
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра автоматизированного оборудования машиностроительного производства
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению контрольных работ по дисциплине
«Физические основы обработки материалов резанием» для студентов направления подготовки бакалавров 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Металлообрабатывающие станки и комплексы») заочной формы обучения
Воронеж 2012
Составители: д-р техн. наук С.Ю. Жачкин, ст. преп. Ю.Э. Симонова
УДК 621.91.02(07)
Методические указания к выполнению контрольных работ по дисциплине «Физические основы обработки материалов резанием» для студентов направления подготовки бакалавров 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Металлообрабатывающие станки и комплексы») заочной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. С.Ю. Жачкин, Ю.Э. Симонова. Воронеж, 2012. 25 с
В методических указаниях изложены требования и общие вопросы по выполнению контрольных работ, составлены задания с необходимыми исходными данными. Выполнение задания дает возможность получения навыков в конструировании и расчетах режущих инструментов с учетом физических особенностей процесса обработки и использованием государственных стандартов, учебной и справочной литературы.
Предназначены для студентов 2 курса.
Методические указания подготовлены в электронном виде в текстовом редакторе MS WORD 97 и содержатся в файле 01.doc.
Табл.2 Ил. 2. Библиогр. 7 назв.
Рецензент канд. техн. наук, доц. Л.А. Иванов
Ответственный за выпуск зав. кафедрой профессор, В.М. Пачевский
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный технический университет», 2012
2
1. ЦЕЛЬ И ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа по курсу «Физические основы обработки металлов резанием» имеет своей целью закрепить теоретические знания, научить студентов самостоятельно решать инженерные задачи по расчету типового и специального режущего инструментов с использованием стандартных методик.
При выполнении контрольной работы студенты решают задачи по выбору типа и конструкции инструмента, материала его режущей части, назначению оптимальных геометрических и конструктивных параметров инструмента при работе в условиях автоматизированного производства с учетом физических особенностей процесса обработки материалов.
В работе могут быть отражены вопросы исследовательского характера: изменение точности при обработке деталей в зависимости от переточек инструмента, влияние геометрических параметров инструмента на точность обработки, точность позиционирования инструмента, способы повышения стойкости инструмента и др.
2.СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ
ИТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
Контрольная работа включает: расчет геометрических параметров, обеспечивающих заданные физические параметры обработки режущими инструментами.
Предлагаемые задания разделены на 2 группы. Каждая группа состоит из пятнадцати вариантов. Задания выдаются преподавателем индивидуально.
Исходные данные, необходимые для проектирования, но не указанные в задании, выбираются самостоятельно по рекомендованной литературе.
Выполненная контрольная работа должна состоять из расчетно-пояснительной записки.
3
Расчетно-пояснительная записка выполняется на писчей бумаге формата А4 и должна содержать задание на проектирование; оглавление; расчет инструмента; список литературы и стандартов.
Расчетная часть должна включать расчет параметров инструмента, требуемых по заданию; обоснование выбора размеров и конструктивных особенностей инструмента, которые не подлежат расчету; обоснование выбора материала и геометрических параметров режущей части инструмента. Расчеты и обоснования должны быть конкретными, при необходимости содержать поясняющие рисунки, их следует подтверждать ссылками на соответствующие литературные источники с указанием страниц, номеров таблиц и т.д.
Графическая часть (при необходимости) выполняется на отдельных листах. Форматы, масштабы изображений и общие требования графического материала должны соответствовать стандартам ЕСКД.
3. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Контрольная работа № 1. |
П о и с к |
о п т и - |
м а л ь н ы х р а з м е р о в |
д е р ж а в к и т о - |
|
к а р н о г о о т р е з н о г о р е з ц а . |
|
|
Выражения для поперечной силы и изгибающего момента в каком либо сечении рациональнее всего получать, используя метод сечений. С этой целью державку разрезают (мысленно) в выбранном сечении на две части и, рассматривая равновесие любой части, получают выражения для Qy и M x .
Отметим, что с целью уменьшения вероятности ошибки, желательно составлять уравнения равновесия таким образом, чтобы каждое содержало только одну неизвестную – Qy , или M x .
Державку разделяют на участки, в пределах которого внешнюю нагрузка постоянна или меняется монотонно. Ис-
2
пользуя метод сечений, на каждом участке получают выражения для Qyi и M xi . При этом для каждого участка можно вы-
бирать свою систему координат. Заметим, что поскольку Qyi и M xi связаны с внешними силами дифференциальными зави-
симостями, приведенными в учебниках по сопротивлению материалов:
|
dQyi |
qi |
Zi |
, |
dM xi |
Qyi |
, |
(1) |
|
dZi |
dZi |
||||||
|
|
|
|
|
|
|
||
то после получения выражений для Qyi и M xi |
полезно |
|||||||
провести их проверку, используя зависимости (1). Перемещения державки при изгибе определяются уг-
лом поворота поперечного сечения 
и прогибом v – вертикальным перемещением. Их положительные направления показаны на рис.1. Прогиб и угол поворота связаны между собой и внутренними силовыми факторами. Между ними имеют место дифференциальные зависимости:
|
d |
|
|
M x |
; |
|
dV |
|
; |
(2) |
||||
|
dZ |
|
EI x |
|
dZ |
|||||||||
|
|
|
|
|
|
|||||||||
После интегрирования согласно зависимостям (2) полу- |
||||||||||||||
чаем выражения для перемещений на каждом участке: |
|
|
||||||||||||
i = Сi + |
M x i |
dZ , V i = Di +СiZi + |
|
|
|
M x i |
|
dZ dZ . |
||||||
E I x |
li |
|
E I x |
|||||||||||
|
|
|
|
|
|
|
|
|||||||
li |
|
|
|
li |
|
|
||||||||
Проинтегрировав выражения для и V |
на каждом из |
|||||||||||||
на n участков, имеем 2n постоянных интегрирования, для нахождения которых необходимо решать систему из 2 n алгебраических уравнений. Более простое решение получаем, составляя единые для всей державки выражения для Qy и M x с
использованием функции Хевисайда H Z Zk . функция Хе-
висайда – разрывная функция, определяемая следующим образом :
3
|
0 |
при |
Z |
Zk |
H Z Zk |
0.5 |
при Z Zk , причем, |
||
|
1 |
при |
Z |
Zk |
Z
H Z Zk dZ Z Zk .
0
В этом случае при известном выражении изгибающего момента для всей державки условия стыковки между участками выполняются автоматически и тогда после интегрирования необходимо определять всего две постоянных (для статически определимой державки) из условий закрепления державки.
Пример выполнения работы.
Дано: а 1,5м, b |
2м, с 3м, М 20кНм, q 10kHм . |
160МПа, Е |
2,1 105 МПа . |
4
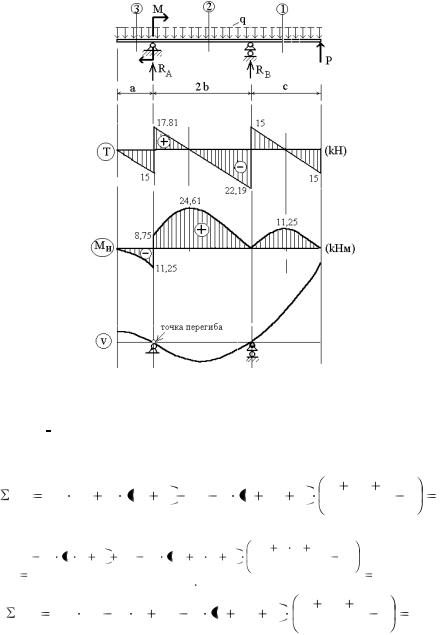
Построение диаграмм поперечных сил Т и изгибающих мо-
ментов М И .
Следует соблюдать масштаб изображаемых величин. Реакции:
|
mA |
|
|
RB 2b P 2b c M q a 2b c |
|
a |
2b c |
a 0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
2 |
2 |
3 |
20 |
10 |
1,5 |
2 |
2 |
3 |
1,5 |
2 |
2 |
1,5 |
|
1,5 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
R |
|
|
|
|
|
|
|
2 |
|
|
|
37,19 kH . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
m |
|
|
|
R |
|
2b P c M q a 2b c |
|
|
a |
2b |
c |
c 0 |
, |
|||||||||||||
|
B |
|
A |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
3 |
20 |
10 |
1,5 |
2 |
2 |
3 |
1,5 |
2 |
2 |
1,5 |
3 |
|
||
|
|
|
|
|
|
|
||||||||||
R |
|
|
|
2 |
|
32,81kH . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверка:
Y RA |
RB P q a |
2b |
c |
32,81 |
37,19 |
15 |
10 8,5 0 |
|||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построение диаграмм Т и М И . |
|
|
|
|
|||||||||||||||||
|
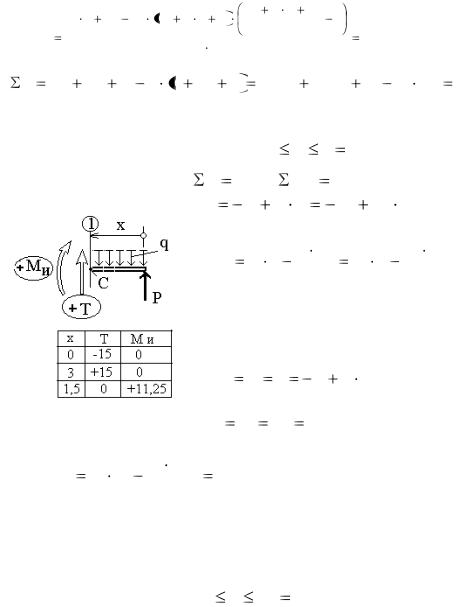
Сечение 1. (правая часть) |
0 |
|
|
х |
с |
|
3м , |
|
|
|
|||||||||||
Из уравнений равновесия: |
|
|
Y |
0, |
|
|
|
mC |
0 следует |
|||||||||||||
|
|
|
|
|
T |
|
P |
|
q |
|
|
|
x |
|
15 |
10 |
х , |
|||||
|
|
|
|
|
(прямая) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
M И |
|
P х |
|
|
|
q |
х 2 |
|
15 х |
10 х 2 |
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
. (парабола) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Парабола имеет экстремум (мак- |
|||||||||||||||||
|
|
|
|
|
симум или минимум), где еѐ про- |
|||||||||||||||||
|
|
|
|
|
изводная равна нулю. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
dM |
|
T |
0 |
|
|
|
|
P |
|
q |
x0 , |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
P |
15 |
|
|
|
1,5 м |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
q |
10 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( М И )хо |
15 1,5 |
10 1,5 |
2 |
|
11,25кНм |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вначале следует построить диаграмму Т , затем, видя распределение касательных функции М И , изобразить еѐ.
Результаты вычислений, по которым строятся диаграммы, рекомендуется представлять таблицей.
Сечение 2. (правая часть) 0 х 2b 4м ,
6
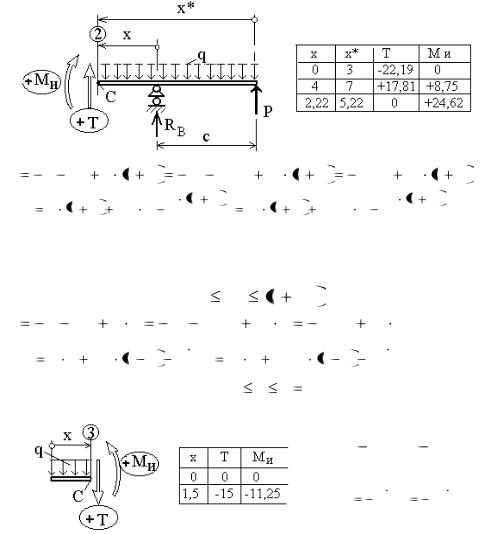
Координату сечения отсчитываем от опоры.
T |
P |
RB |
q |
ñ |
õ |
|
|
15 |
37,19 |
10 |
c |
x |
42,19 |
10 |
3 x |
|||||||
M И |
P |
c |
x |
RB |
x |
|
q |
x |
c 2 |
15 |
3 |
x |
37,19 |
x |
10 |
3 |
x 2 |
|||||
|
|
2 |
|
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Текущую координату сечения можно отсчитывать от конца |
|
|
||||||||||||||||||||
стержня. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом: |
|
|
|
|
|
c |
х* |
|
c |
2b , |
|
|
|
|
|
|
|
|
||||
T |
P |
RB |
q х |
|
15 37,19 |
10 х |
|
42,19 |
|
10 |
х , |
|
|
|||||||||
M И |
P х |
RB |
х |
с |
|
|
q х 2 |
15 |
х |
37,19 |
х 3 |
|
|
10 х 2 |
. |
|
|
|||||
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
Сечение 3. (левая часть): 0 |
х |
а |
1,5м , |
|
|
|
|
|
|
|
|
||||||||||
T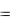 
q 
х 
10 
х
M И |
q х 2 |
10 х 2 |
||
2 |
|
2 |
||
|
||||
Изображение изогнутой оси державки.
Без количественной оценки перемещений поперечных сечений державки еѐ изогнутую ось изображаем по распределению изгибающих моментов по длине, зная, что в опорных уст-
7
ройствах возможен поворот и линейные перемещения отсутствуют (если опоры не перемещаются), а в защемлении отсутствуют оба перемещения. Необходимо учитывать: положитель-
ному моменту соответствует положительная кривизна и наоборот; смена кривизны (точка перегиба), где изгибающий момент равен нулю; кривизна там больше, где больше изгибающий момент.
Определение размеров поперечного сечения стержня из условия прочности:
|
М И |
yМАХ |
. |
МАХ |
J Z |
||
|
|
|
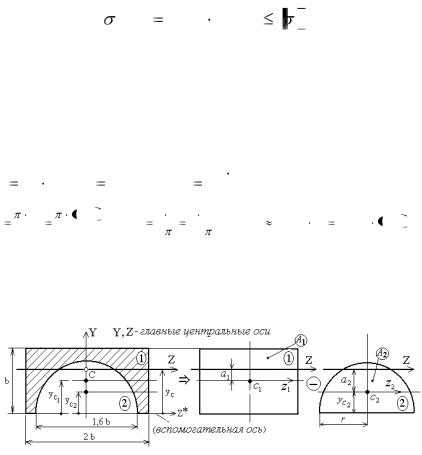
Геометрические характеристики поперечного сечения.
Изгиб осуществляется относительно главной центральной оси Z, положение которой необходимо определить. Сечение образовано из двух элементарных фигур: прямоугольника и полукруга, для которых геометрические характеристики обычно известны:
A1 |
2b b, |
yc |
0,5b; |
J z |
|
2b |
b3 |
|
, |
|||||
12 |
|
|||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
r 2 |
0,8b 2 |
, y |
|
4 r |
4 0,8b |
, |
J |
0,1098 r 4 0,1098 0,8b 4 |
|||||
|
|
|
|
c2 |
|
|
|
|||||||
2 |
2 |
|
|
2 |
|
3 |
|
3 |
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определим положение центра тяжести всего сечения относительно вспомогательной оси (см. рисунок):
8