Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 429

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

417.44 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

f (t)= r(t −τ)η(t −τ).

Пример. Восстановить оригинал

f (t) по его изображению

R(p)=

e−2 p

(p2

+1)2

Решение. 1. Восстанавливаем оригинал r(t)

по его изобра-

жению R(p)=

(p2 +1)2

Имеем

sin t ↔

2 +1

По теореме умножения изображений

sin t sin t ↔

p2 +1

Вычисляем свертку

sin t sin t = ∫sin(t −τ)sinτ dτ =

t cost −

sin t.

Таким образом,

r(t)=

t cost −

sin t.

2. По теореме запаздывания искомый оригинал определяется формулой

f (t)= r(t −2)η(t −2)= 12 [(t −2)cos(t −2)−sin(t −2)−sin(t −2)]η(t −2)

Ответ.

f (t)= 12 [(t − 2)cos(t − 2)−sin(t − 2)−sin(t − 2)]η(t − 2).

Условия задач. Восстановить оригинал f (t) по его изображению F(p).


1.	F(p)=		e− p			.
			p2 +1

3.	F(p)=	e−7 p		.

		p −3
5. F(p)=			e−3 p
		p(p2 +9)
7.	F(p)=		pe− p		.

		p2 −3
9. F(p)=			pe−6 p
							.
		(p2 + 4)(p2 +1)

2.	F(p)=					pe−4 p			.

						p2 +1
4.	F(p)=				2e−5 p			.

					p2 − 4
		e	−		p
6.	F(p)=			2			.
		p4			−1


	F(p)=		e−3 p
8.				.
		p2 (p2 −1)
10.	F(p)=		pe−πp		.
			(p2 +16)2

12. Решение линейных дифференциальных уравнений

Постановка задачи. Найти решение задачи Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами

an x(n) + an−1 xn−1 +... + a1 x′+ a0 x = f (t)

с начальными условиями

x(0) = x0 , x′(0) = x0′, ..., x(n−1) (0) = x0(n−1) .

План решения. Если f(t) – оригинал, то искомое решение дифференциального уравнения x(t) также является оригиналом. Обозначим его изображение X (p).

1. Находим изображение левой части уравнения. По теореме о дифференцировании оригинала

′	′′	2		′
x (t) ↔ pX ( p) − x(0),	x (t) ↔ p		X ( p) − px(0) − x (0) , …,
x(n) (t) ↔ pn X ( p) − pn−1 x(0) −... − xn−1 (0).
По свойству линейности
an x(n) + an−1 x(n−1) +... + a1 x′+ a0 x ↔
↔ (an pn + an−1 pn−1 +... + a1 p + a0 )X (p)− pn−1 x0				− pn−2 x0′ −... − x0(n−1).

2. Находим изображение правой части уравнения f (t)↔ F(p).

3. Составляем операторное уравнение

(an pn + an−1 pn−1 +... + a1 p + a0 )X (p)=

= F(p)+ pn−1 x0 + pn−2 x0′ +... + x0(n−1).

4.Решаем операторное уравнение относительно X (p).

5.По найденному изображению X (p) восстанавливаем оригинал x(t).

6.Проверяем, удовлетворяет ли x(t) исходному диффе-

ренциальному уравнению и начальным условиям. Записываем ответ.

Пример. Решить задачу Коши

x	′′	+ 4x = cos 2t , x(0)=1,	′
x		+ 4x = cos 2t , x(0)=1,	x (0)= −1.
Решение.		Так как f (t)= cos 2tη(t)	- оригинал, то искомое

решение дифференциального уравнения x(t) также является оригиналом. Обозначим его изображение X (p).

1. Находим изображение левой части уравнения. По теореме о дифференцировании оригинала

x′(t) ↔ pX ( p) − x(0) = pX (p)−1,

x′′(t) ↔ p2 X ( p) − px(0) − x′(0) = p2 X (p)− p +1.

По свойству линейности

x′′+ 4x ↔ (p2 + 4)X (p)− p +1

2. Находим изображение правой части уравнения cos 2t ↔ p2 p+ 4 .

3.Составляем операторное уравнение

(p2 + 4)X (p)− p +1 = p2 p+ 4 .

4. Решаем операторное уравнение относительно X (p):

X (p)=

−

(p2

+ 4)2

2 + 4

2 +

По

найденному изображению

X (p)

восстанавливаем

оригинал x(t):

x(t)=

t sin 2t + cos 2t −

sin 2t .

x(t)

При подстановке

в исходное дифференциальное

уравнение

оно

обращается

тождество.

Вычислив x(0) и

′

удовлетворяет начальным услови-

(0), убеждаемся, что x(t)

ям.

Ответ. x(t)=

t sin 2t + cos 2t −

sin 2t

Условия задач. Решить задачи Коши для дифференциаль-

ных уравнений.

x′+ 2x = 2 −3t ,

x(0)= 0 .

x′− x = t −1,

x(0)= 0 .

x′+3x = 3t − 2 ,

x(0)= 0 .

′

′′

′

x −3x + 2x =

x(0)=1, x (0)= 3 .

′′

+ x

′

= t cos 2t ,

x(0)= 0 ,

′

(0)= 0 .

′′

+9x =1,

x(0)= 0 ,

′

x (0)= 0 .

′′

+ 4x

= sin 3t ,

x(0)= 0 ,

′

x (0)= 0 .

′′′

− x

′′

= 0 ,

x(0)= 2 ,

′

′′

(0)= 0 ,

x (0)=1.

′′′

+ 6x

′′

+11x

′

+ 6x = 0

x(0)=1,

′

′′

′

x (0)= −3 ,

x (0)= 9 .

′′′

′′

′

′′

10. x

−3x

+3x − x = e

x(0)=1,

x (0)= −1,

x (0)=1.

13 Решение систем линейных дифференциальных уравнений

Постановка задачи. Решить задачу Коши для системы обыкновенных линейных дифференциальных уравнений первого порядка с постоянными коэффициентами:

х = Ах(t)+f(t)

с начальными условиями

х(0)=х0,

где х={x1,…,xn} – вектор неизвестных, х0={x01,…,xn0} – вектор начальных значений,

a11		a12	… a1n
А = a21		a22	… a2n

		an2	…
an1				ann
- матрица коэффициентов и f(t) = {f1 (t),..., fn (t)} - заданная
вектор-функция.	f1	(t),..., fn (t) являются оригиналами,
План решения. Если
то функции x1 (t),..., xn (t)	также являются оригиналами. Обо-

значим их изображения X1 (p),..., X n (p).

1.По теореме о дифференцировании оригинала и по свойству линейности находим изображения левых и правых частей всех уравнений системы.

2.Составляем систему операторных уравнений

pX – x0=AX(p) + F(p).

3. Решаем систему операторных уравнений. X(p)=(pE – A)-1(F(p)+x0),

где Е – единичная матрица n-го порядка.

4.По найденным изображениям X(p) = {X1(p), X2(p),…, Xn(p)} восстанавливаем оригиналы x1 (t), x2 (t)..., xn (t)

5.Проверяем, удовлетворяют ли x1 (t), x2 (t)..., xn (t)исходной системе дифференциальных уравнений и начальным условиям.

Записываем ответ.

Пример. Решить задачу Коши

x′ = x +

2 y −9t,

x(0)=1,

y′ = 2x + y + 4et , y(0)= 2.

Решение. Предполагая, что функции x(t)и

y(t)являются

оригиналами, обозначим их изображения X ( p) и Y ( p) .

1. По теореме дифференцирования оригинала

′

↔ pY ( p) − y(0) = pY ( p) − 2

x (t) ↔ pX ( p) − x(0) = pX (p)−1,

y (t)

По свойству линейности находим изображения правых

частей уравнений системы:

x + 2 y −9t ↔ X (p)+ 2Y

(p)−

2x + y + 4et ↔ 2X

(p)+Y (p)+

p −1

2. Составляем систему операторных уравнений:

pX (p)−1

= X (p)+ 2Y (p)

−

pY (p)− 2 = 2X (p)

+Y (p)+

. .

p −1

3. Решаем систему операторных уравнений:

X (p)=

−

p −1

p(p −1)

(p −1)(p +1)

−3)(p −1)

Y (p)= −

−3

4. Восстанавливаем оригиналы по изображениям

X ( p) и

Y ( p) :

x(t)= 2e3t − 4e−t − 2et +5 −3t ,

y(t)= −4 + 6t + 4e−t + 2e3t .

5. При подстановке x(t)и y(t) в исходную систему оба уравнения обращаются в тождества. Вычислив x(0) и y(0), убеждаемся, что x(t) и y(t) удовлетворяют начальным условиям.

Ответ.

x(t)= 2e3t − 4e−t − 2et +5 −3t , y(t)= −4 + 6t + 4e−t + 2e3t .

Условия задач. Решить задачи Коши для систем дифференциальных уравнений.

1.	x′ = y −1,		x(0)=1,			2.	x′ = −y + 2, x(0)= −1,
		′ = −x − 2y, y(0)= −1.						y(0)= 0.
	y						y′ = x +1,
3.	3x′+ 2x + y′		=1, x(0)= 0,		4.		x′− 2 y = 0, x(0)= 2,
			= 0, y(0)= 0.
	x′+ 4 y′+3y						y′− 2x = 0, y(0)= 2.
5.	x′	= 3x + 4 y, x(0)=1,			6.	x′ = 2x +3y +1, x(0)= −1,
							y′ = 4x − 2 y,	y(0)= 0.
	y′ = 4x −3y, y(0)=1.
7.	x′ = −x +3y +1, x(0)=1,					x′+ y = 0,		x(0)=1,
		y′ = x + y,	y(0)= 2.		8.
						y′+ x = 0, y(0)= −1.
9.	x′ = −y,		x(0)=1,	10.		x′	+ y′− y = et ,	x(0)= 0,
		′ = 2x + 2 y,	y(0)=1.
	y				2x′+ y′+ 2 y = cos t, y(0)= 0.
					25

14. Решение интегральных уравнений

Интегральными уравнениями называются такие уравнения, в которых неизвестная функция x(t) стоит под знаком интеграла. В некоторых случаях такие уравнения тоже могут быть решены средствами операционного исчисления.

Уравнения вида

t
f (t) = ∫	k(t, τ)x(τ)dτ	(7)
0
и
	t
x(t) = f (t)	+ ∫ k(t, τ)x(τ)dτ	(8)
	0

называются уравнениями Вольтерра соответственно первого и второго рода. Здесь f (t) , k(t, τ) - заданные функции, x(t) -

неизвестная функция. Функция k(t, τ) называется ядром инте-

грального оператора.

Рассмотрим случаи, когда функция k(t, τ) = k(t − τ) зави-

сит только от разности t-τ, то есть рассмотрим уравнения Вольтерра вида

t
f (t) = ∫	k(t − τ)x(τ)dτ	(9)
0
и
	t
x(t) = f (t) + ∫ k(t − τ)x(τ)dτ,		(10)
	0
причем будем предполагать,	что функции f (t) и	k(t) явля-

ются оригиналами. Применим преобразование Лапласа к правой и левой частям уравнений (9) и (10), при этом воспользуемся теоремой об умножении изображений. В результате получим

F( p) = K( p) X ( p)	для уравнения (9)
и	26

X ( p) = F( p) + K( p) X ( p) для уравнения (10).

Отсюда следует, что

X ( p) =	F( p)	или X ( p) =		F( p)	.
	K( p)		1	− K( p)

Неизвестная функция x(t) находится с помощью обратного преобразования Лапласа.

Пример 1. Решить интегральные уравнения:

t	t
а) ∫et −τ x(τ)dτ = t ; б)	x(t) − ∫(t −τ)x(τ)dτ =sin t .
0	0

Решение: а) Интеграл, стоящий в левой части уравнения, представляет собой свертку функций е t и x(t). Пусть x(t) ↔ X(p). Тогда по теореме о свертке получим изображение интеграла

∫et −τ x(τ)dτ

= et * x(t) ↔

X ( p) ;

p −1

Составим теперь операторное уравнение:

X ( p) =

p −1

p 2

откуда

X ( p) =

p −1

−

Следовательно, x(t) = 1 – t.

б) Пусть x(t) ↔ Х(р). По таблице изображений находим

t ↔	1	и sin t ↔	1
	p2		p2 +1

По теореме о свертке получим изображение интеграла:

t	1
∫(t −τ)x(τ)dτ = t * x(t) ↔		X ( p) .
	2
0	p

Составляем операторное уравнение

X ( p) −	1	X ( p) =	1	.
	p 2
			p 2 +1

Решая его относительно функции Х(р), находим

			p 2				1		1				1
X ( p) =						=					+				.
		2		2					2				2
	( p		−1)( p		+1)		2			−1		p		+1
								p

Находя оригинал для функции X (р), получаем решение исходного интегрального уравнения

x(t) = 12 (sh t + sin t).

Пример 2. Найти решение интегрального уравнения

x(t)

= sin t

+ ∫

(t − τ)x(τ)dτ.

Решение: Это уравнение Вольтерра второго рода. Так как

∫ (t − τ)x(τ)dτ = t * x(t) , то переходя к изображениям,

получим

X ( p)

X ( p) =

p2 +1

Отсюда находим, что

X ( p) =

( p

−

1)( p

+1)

−1

Следовательно, x(t) =

1 (sh t +sin t) .

Условия задач: Решишь интегральные уравнения:

1. ∫et −τ x(τ)dτ = sin t. 2.

∫cosτ x(t −τ)dτ =sin t.

	t		t
3.	∫cos(t −τ)x(τ)dτ = t 2 . 4. ∫e2(t −u) x(u)du = t 2 et .
	0		0
	t
5.	∫(t −τ)x(τ)dτ − x(t) = −cos t.
	0
	t
6.	x(t) = ∫et −τ x(τ)dτ + cos t .
	0
	t
7.	∫(t −τ)2 x(τ)dτ − 2x(t) + 2et = 0.
	0
	t
8.	x(t) − 2∫[(t − u) − sin(t − u)]x(u)du = t .
	0
	t
9.	∫(1 − 2(t −τ))x(τ)dτ − x(t) = 2(1 + t − et ) .
	0	1 t
		1 t
10. x(t) =1 +			∫(t − u)3 x(u)du .
10. x(t) =1 +		6	∫(t − u)3 x(u)du .
		6	0

15. Нахождение изображений функций, заданных графиком

При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматического регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции, привести полученное выражение к виду, удобному для применения табл.1 и свойств преобразования Лапласа.

Пример 1. Найти изображения функций, заданных графиками на рис. 1.

а) Представим функцию в виде

f (t)= (1−t) 1(t −1)= (t −1) 1(t −1).

По формуле 3 из табл.1 и теореме запаздывания

F(p)= − p12 e−p .

б) Запишем функцию в виде

f (t)= (1−t)[1(t)−1(t −1)]= (1−t) 1(t)+(t −1) 1(t −1).

По формулам 1,3 из табл. 1

F(p)= 1p − p12 + p12 e−p .

в) Запишем изображенную функцию в виде

f (t)= −t 1(t −1)= (−t +1−1) 1(t −1)= −(t −1) 1(t −1)−1(t −1).

По формулам 1,3 из табл.1

F(p)= − p12 e− p − 1p e− p .

г) Представим функцию в виде

f (t)= (t −1)[1(t −1)−1(t − 2)]+ (3 −t)[1(t − 2)−1(t −3)]= = (t −1) 1(t −1)− 2(t − 2) 1(t − 2)+ (t −3) 1(t −3).

По формулам 3 из табл. 1

F(p) =	e− p	−	2e−2 p	+	e−3 p	.
	p2		p2
					p2
			30

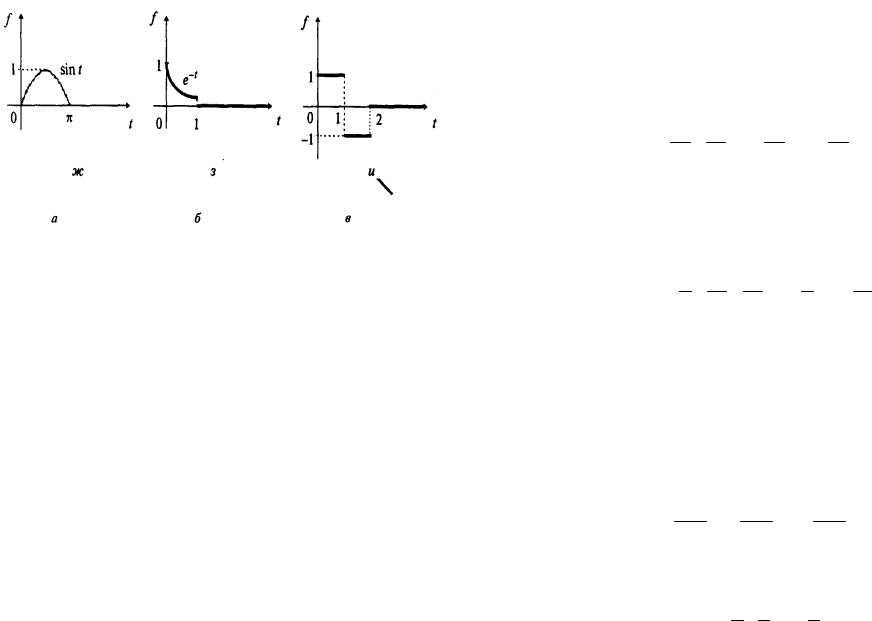
Рис. 1

д) Запишем функцию в форме

f (t)= t[1(t)−1(t −1)]+[1(t −1)−1(t − 2)]+(3 −t)[1(t − 2)−1(t −3)]=

=t 1(t)−(t −1) 1(t −1)−1(t −1)+ 1(t −1)−1(t − 2)+ + (2 −t) 1(t − 2)+ 1(t − 2)−(3 −t) 1(t −3)=

=t 1(t)−(t −1) 1(t −1)−(t − 2) 1(t − 2)+ (t −3) 1(t −3).

По формулам 3 из табл. 1

F(p)= p12 − p12 e−p − p12 e−2 p + p12 e−3 p .

е) Представим изображенную функцию в виде

f (t) = (1 −t)[1(t)−1(t −1)]−1 [1(t −1)−1(t − 2)]+ (t −3) 1(t − 2) = = (1 −t) 1(t)+ (t −1) 1(t −1)−1(t −1)+1(t − 2)+ (t − 2) 1(t − 2)−

−1(t − 2) = (1 −t) 1(t)+ (t −1) 1(t −1)−1(t −1)+ (t − 2) 1(t − 2).

По формулам 1,3 из табл. 1

F(p)= 1p − p12 + p12 e−p − 1p e−p + p12 e−2 p .

ж) Запишем функцию в форме

f (t)= sin t[1(t)−1(t − π)]= sin t 1(t)+ sin(t − π) 1(t − π).

По формуле 8	из табл. 1 и по теореме запаздывания
	F(p)=	1	+	e−πp	.
	F(p)=	p2 +1	+	p2 +1	.
		p2 +1		p2 +1
з) Представим функцию в виде
f (t)= e	−t [1(t)−1(t −1)]= e−t 1(t)− e−(t−1)					1(t −1).
					e

По формуле 6 из табл. 1

F(p)= p1+1 − 1e p1+1 e−p = p1+1 (1 −e−p−1 ).

и) Представим функцию в виде

f (t) =1 [1(t) −1(t −1)] −1 [1(t −1) −1(t − 2)] = 1(t) − 2 1(t −1) +1(t − 2).

Используя формулы 2 из табл.1, получим

F( p) = 1p − 2p e− p + 1p e−2 p.

		Ответы для заданий
		Раздел 1
1.	F(p) = (1 – e-p)/p.	2. F(p) = (1 - 2e-P + e-2P)/p.
3.	F(p) = (e-P + e-3p)/p.	4. F(p) = (1 - e-p – pe-p/p2.
5.	F(p) = (l-e-P-2pe-P+p)/p2 .	6. F(p) = (1+ e-2p+pe-2p-p)/p2.
7.	F(p) = (l-e-p)/(p+pe-p).	8. F(p) = (e-p-e-2P + 2pe-2p)/p2.
9.	F(p) = (1 - 2e-p + e-2p)/p2.	10. F(p) = e-p/(p+ 1).

Раздел 2

l. F(p) = l/(p2+l). 2. F(p) = p/(p2-1). 3. F(p) = l/(p2-l).

4. F(p) = (cos φ+ p sin φ))/(p2 + l). 5. F(p) = (p cos φ-sin φ)/(p2 + 1).

6.F(p) = (8p2 + 6p + 5)/(p3 + 2p2 + p + 2).

7.F(p) = (p + l)/(p2 + 1). 8. F(p) = 2/(p4-l). 9. F(p) = 2p/(p4-l).

10.F(p)=(2p2 + l)/(2p3 + 2p).

Раздел 3

1. F(p) = 2/(p2 + 4). 2. F(p) = p/(p2 - 4). 3. F(p) = 2/(p2 - 4).

4. F(p) = 2/(4p2 + 1). 5. F(p) = 4p/(4p2 + 1). 6. F(p) = 2/(p3 + 4p). 7. F(p) = (p2 + 2)/(p3 + 4p).8. F(p)=(3p2+15)/(p4+26p2+25).

9. F(p)=(ωcosφ+psinφ)/(p2+ω2).10.F(p)=(pcosφ+ωsinφ)/(p2+ω2).

Раздел 4

1. F(p) = 3/(p2-4p+13). 2. F(p) = (p + 4)/(p2 + 2p+10).

3.F(p) = =(p2-2p+3)/[(p-l)(p2-2p+5)]. 4.F(p)=2/[(p-3)(p2-6p+13)]. 5.F(p) = =(p — a)/(p2 — 2ap + a2 + ω2). 6. F(p) = ω /(p2- 2ap + a2 + ω2).

7.F(p) = (ωcosφ + (p — a)sinφ)/(p2 - 2pa + a2 + ω2).

8.F(p) = [(p — a) cosφωsinφ]/(p2- 2pa + a2 + ω2). 9.F(p)=p /(p + 4 ω ).

10.F(p) = 2 ω2p/(p4 + 4 ω4).

Раздел 5

1. F(p) = e-p/p3. 2. F(p) = pe-2p/p2 + 1. 3. F(p) = (1 - 2e-p + e-2p)/p.

4. F(p) = (1 – e-2p/p2. 5. F(p) = (l-2e-p + e-2p)/p2. 6. F(p) =e-p/(p + l). 7. F(p) =e-p/(p2 +p). 8. F(p) = (l-e-p)/(p + pe-p).

9. F(p)=(1+e-πp)//[(p2+1)(1-e-πp)]. 10. F(p)=(p+e-πp/2-pe-πp)/[(p2+1)(1-e-πp)].

Раздел 6 1. F(p)=2ωр/(р2+ω2)2. 2. F(p =(p2-ω2)/(p2+ω2)2.

3. F(p =2ωp/(p2 -ω2)2. 4. F(p= (p2 + ω2)/(p2 - ω2)2. 5. F(p) = 2/(p - a)3. 6. F(p) =(6ωp2 - 2ω3)/(p2 + ω2)3. 7. F(p) = (2p3 - 6ω2p)/(p2 + ω2)3. 8.F(p) =(6ωp2 + 2ω3)/(p2 - ω2)3. 9. F(p) = (2p3 + 6ω2p)/(p2 - ω2)3. 10. F(p) = n!/(p - a)n+1.

Раздел 7

1. F(p) = ln

− a

. 2. F(p)= ln

p2 + 4

. 3.F(p)= arctg

p + a

4. F(p)=

. 5. F(p)=

−1

. 6. F(p)=

−1

7. F(p)=

. 8. F(p)=

+100

. 9.

p − a

+ 25

+16

p −b

10. ln

(p − a)2

+ 4

Раздел 8

1. f(t) = e2t

+ е-t /2. 2. f(t) = t + 2 - 2et + tet

. 3. f(t) = -1 +

+4e-2t cos3t

- e-2t sin3t /3. 4. f(t) = et/9 - e2t /9 + 2te-2t /3. 5. f(t) =

= -5еt /6 + 8е-2t /15 + 13е3t/10. 6. f(t) =2et-4t -3.7. f(t)=t2et/2.

8. f(t)= (ch t - cos t) /2. 9. f(t) = (3t2 + 2t

- 2)et /54+(2t+ l)e-2t /27.

10. f(t) = -1/6 + et

- 3e2t /2 + 2e3t /3.

Раздел 9

1. f(t)=t2et/2. 2. f(t)=-1/6+et-3e2t/2+2e3t/3. 3. f(t)=-et/3+e2t/4+e-2t/12.

4. f(t)=1-2et+e3t. 5. f(t)=(3-4cost+cos2t)/12. 6. f(t)=-1/6-3e-3t/2+2e-4t/3+e-2t. 7. f(t)=2et-4t-3. 8. f(t)=-1/6+et/2-e2t/2+e2t/6. 9. f(t)=(e3t-e-t)/4. 10. f(t)=1-e-t-te-t.

Раздел 10

1. f(t) = (sin2t-2t cos2t)/4. 2. f(t) = (sin3t-3t cos3t )/6. 3. f(t)= (t cht -3t sht + 2t )/2. 4. f(t) = (3sin3t - 2sin2f)/5. 5. f(t)=(ch t - cos t)/2. 6. f(t) = (sin t+ t cos 3t)/2.

7. f(t)=(1 - cost ) η (t - 1). 8. f(t) = (t -l- sin(t - l))η(t - 1).

9.f(t) = (1 - cos(t -l)-(t -l) sin(t - l)/2)η(t - 1).

10.f(t) = (l- cost)η (l - t ) + (cos(t - 1) - cost )η (t - 1).

Раздел 11

1. f(t) = sin(t - 1)η(t - 1). 2. f(t) = cos(t - 4) η (t - 4). 3. f(t) = e3(t -7) η (t - 7). 4. f(t)=sh2(t - 5) η(t - 5).

5.f(t) = (1 - cos(3t - 9))η(t - 3)/9.

6.f(t) = (sh(t -1/2)-sin(t - l/2))η(t - l/2)/2.

7.f(t) = ch( 3 (t - l)) η(t - 1).

8.f(t)=(sh(t - 3)-t -3)η(t -3). 9. f(t)= (cos(t-6)-cos(2t -12))η(t - 6).

10.f(t) = (t -π) sin(4t - 4 π) η(t - π)/8.

Раздел 12

1. x(t)=1,75-1,5t-1,75e-2t.2. x(t)=-t. 3. x(t)=e-3t+t-1. 4. x(t)=e3t. 5. x(t)=-(5/9)sint+(4/9)sin2t-(t/3)cos2t. 6. x(t)=(1/9)(1-cos3t). 7. x(t)=(3/10)sin2t-(1/5)sin3t. 8. x(t)=1-t+et. 9. x(t)=e-3t.

10. x(t)=et(t3/6+1-2t+2t2).

Раздел 13

1.x(t)=3e-t+te-t-2, y(t)=1-2e-t-te-t.

2.x(t)=2sint-1, y(t)=2-2cost.

3.x(t)=(1/2)-(1/5)e-t-(3/10)e-6t/11, y(t)=(1/5)(e-t-e-6t/11).

4.x(t)=(5/2)e2t-(1/2)e-2t, y(t)= (5/2)e2t-(1/2)e-2t.

5.x(t)=(6/5)e5t-(1/5)e-5t, y(t)= (3/5)e5t-(2/5)e-5t.

6.x(t)=-(1/8)-(9/16)e4t-(5/16)e-4t, y(t)= -(1/4)-(3/8)e4t+(5/8)e-4t.

7.x(t)=(15/8)e2t-(9/8)e-2t+(1/4), y(t)=(15/8)e2t+(3/8)e-2t-(1/4).

8.x(t)=et, y(t)=-et.

9.x(t)=et(cost+4sint), y(t)=et(cost+3sint).

10.x(t)=et-(11/34)e4t-(3/17)cost+(5/17)sint-1/2,

y(t)=-(2/3)et+(22/51)e4t+(4/17)cost-(1/17)sint.

N f(t)

1 2

1I (t)

4t n

5δ(t)

6eat

7t neat

8sin at

9cos at

10t sin at

11t cosat

Таблица преобразований Лапласа

Таблица 1

F(p)

f(t)

F(p)

eat sin bt

( p −a)

eat

cosbt

p − a

(p − a)2

+ b2

1 e−t / a

1 + ap

−1)

p(p − a)

n+1

eat −ebt

a −b

(p − a)(p − b)

(1−cos at)

p(p2 + a2 )

p −a

(eat −1 − at)

(p − a)

( p −a)n+1

shat

− a2

p2 +a2

chat

− a2

p2 +a2

2 pa

( p2 +a2 )2

(p −a)

p2 −a2

1 2

(1+ 2at +

( p − a)3

( p2 +a2 )2

Продолжение табл. 1

(1+ at)eat

aeat

−bebt

( p − a)( p −b)

(p − a)2

a −b

cos

+2a

asin bt −bsin at

a2 −b2

( p2 + a2 )( p2 +b2 )

p( p2 +4a2 )

sin 2 at

2a2

cosbt −cosat

a2 −b2

( p

+ a )( p

)

p( p2 +4a2 )

a2 p

asin at −bsin bt

sin

2 t sh

2 t

a2 −b2

( p2 + a2 )( p2 +b2 )

p4 +a4

a2 cosat −b2 cosbt

cos

2 t ch

2 t

a2 −b2

( p2 + a2 )( p2 + b2 )

p4 +a4

1 (shat −sin at)

bshat −ashbt

( p

2 −a

2 )( p2

−b2 )

a2 −b2

p4 −a4

1 (chat −cos at)

chat −chbt

( p

2 −a

2 )( p2

−b2 )

a2 −b2

p4 −a4

(shat +sin at)

ashat −bshbt

−b

( p2 −a2 )( p2 −b2 )

p4 −a4

1 (chat +cos at)

chat −b

chbt

( p2 − a2 )( p2 −b2 )

−b

p4 −a4

Продолжение табл. 1

a 2

t −

sin at

p 2 ( p 2

+ a 2 )

shat −t

a 2

p 2 ( p 2

− a 2 )

1 −cos at −

sin at

a 4

p( p 2 + a 2 )2

1 −chat +

shat

p( p2 − a2 )2

1 +

cos at

− a

cosbt

a2 −b2

p( p 2 + a 2 )( p 2 + b2 )

1 +

chat − a

chbt

a2 −b2

p( p 2 − a 2 )( p 2 − b2 )

(c −b)eat + (a −c)ebt + (b − a)ect

( p − a)( p − b)( p − c)

(a −b)(a −c)(c −b)

a(b −c)eat +b(c − a)ebt + c(a −b)ect

(a −b)(b −c)(a −c)

( p − a)( p − b)( p − c)

a2 (b −c)eat +b2 (c − a)ebt + c2 (a −b)ect

p 2

(a −b)(b −c)(a −c)

( p − a)( p − b)( p − c)

(sin at − at cos at)

2a3

( p 2 + a 2 )2

(sin at + at cos at)

p 2

( p 2 + a 2 )2

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022415.84 Кб2Учебное пособие 424.pdf
#
30.04.2022416.2 Кб2Учебное пособие 425.pdf
#
30.04.2022416.28 Кб2Учебное пособие 426.pdf
#
30.04.2022416.61 Кб6Учебное пособие 427.pdf
#
30.04.2022416.63 Кб5Учебное пособие 428.pdf
#
30.04.2022417.44 Кб3Учебное пособие 429.pdf
#
30.04.2022243.65 Кб2Учебное пособие 43.pdf
#
30.04.2022418.46 Кб3Учебное пособие 430.pdf
#
30.04.2022419.91 Кб3Учебное пособие 431.pdf
#
30.04.2022420.4 Кб4Учебное пособие 432.pdf
#
30.04.2022420.91 Кб2Учебное пособие 433.pdf