
Методическая разработка к контрольной работе № 1 по дисциплине «Математика» для студентов направлений подготовки бакалавров. Горбунов В.В., Костина Т.И
.pdf
Таким образом, уравнение плоскости A1A2A3 имеет вид
21x 9y 3z 48 0.
Составим уравнение прямой, проходящей через точки A1 и A4. Уравнение прямой, проходящей через две точки, имеет вид
|
x x1 |
|
y y1 |
|
|
z z1 |
, |
|
|
|||||||||||
|
|
|
y4 y1 |
|
|
|
|
|
||||||||||||
|
x4 x1 |
|
|
|
|
|
z4 z1 |
|
||||||||||||
где (x1, y1,z1) – координаты точки A1, (x2,y2,z2) |
– координаты |
|||||||||||||||||||
точки A4. Подставляя в уравнение координаты точек A1 и A4, |
||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x 2 |
|
|
y 1 |
|
z 1 |
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||||||
Угол между прямой |
|
x x1 |
|
y y1 |
|
|
z z1 |
|
и плоскостью |
|||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
m |
|
|
n |
|
||||||
Ax By Cz D 0 определяется по формуле
sin
Al Bm Cn

 A2 B2 C2
A2 B2 C2 
 l2 m2 n2
l2 m2 n2
Воспользуемся этой формулой для вычисления угла
между ребром |
A1A4 |
и плоскостью A1A2A3: |
|
|
|
|
|
|
|
|
|
|||||||||
sin |
|
|
( 21) 2 |
9 2 3 2 |
|
|
|
|
18 |
|
|
|
|
3 |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( 21)2 92 |
|
32 22 22 |
22 |
531 12 |
177 |
|
|
|||||||||||
3
Отсюда arcsin .
 177
177
4) Уравнение высоты найдем как уравнение прямой, проходящей через точку A4 перпендикулярно плоскости
A1A2A3 , задаваемой уравнением |
Ax By Cz D 0. Из |
29 |
|

условия перпендикулярности прямой и плоскости следует
|
A |
|
B |
|
C |
, поэтому уравнение высоты A D имеет вид |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
l m |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x 4 |
|
|
|
|
y 1 |
|
|
z 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Для нахождения длины высоты можно использовать |
||||||||||||||||||||||||||||||||||
формулу |
|
V |
1 |
S |
|
|
|
|
|
|
|
. |
Объем |
|
V |
и |
площадь S |
|
|
|
|||||||||||||||||
|
A A A |
|
A D |
|
A A A |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3V |
|
|
|
18 |
|
|
1 |
2 |
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
будут найдены в п.5). Поэтому |
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||
|
A D |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
SA1A2 A3 |
|
|
531 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5) |
Грань |
A1A2A3 |
|
представляет |
собой |
|
треугольник, |
||||||||||||||||||||||||||||||
площадь которого равна половине площади параллелограмма,
построенного на векторах A1A2 |
|
и A1A3 . |
|
|
|
|
|
|||||||||||||||||||||||||||
Найдем векторное произведение этих векторов. Имеем |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
21,9,3 . |
||||||||||
A1A2 A1A3 |
|
|
3 |
|
6 |
|
|
3 |
|
21i |
9j 3k |
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
( 21)2 |
92 |
32 |
|
|
|
|
. |
||||||||||||||||
|
A A |
A A |
|
|
|
|
|
|
|
531 |
||||||||||||||||||||||||
|
1 |
2 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
531 |
. |
|||||||||||||
|
S |
A A A |
|
|
|
A A |
|
A A |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
1 2 |
|
1 3 |
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для вычисления объема пирамиды воспользуемся смешанным произведением векторов. Напомним, смешанное произведение трех векторов по модулю равно объему параллелепипеда, построенного на этих векторах. А объем
пирамиды равен 1 части объема этого параллелепипеда. 6
Имеем
30

|
|
|
3 |
6 |
3 |
|
A1A2 A1A3 A1A4 |
1 |
3 |
2 |
18. |
||
|
|
|
2 |
2 |
2 |
|
Поэтому V 1 | 18| 3.
6
Задача №3
Даны координаты вершин треугольника ABC: A( 8,3),
B(4, 6), C(2,8). Найти:
1) уравнения сторон AB и |
AC и их угловые |
коэффициенты; |
|
2)угол A в радианах (градусах) с точностью до двух знаков после запятой;
3)уравнение высоты CD и ее длину;
4)уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD.
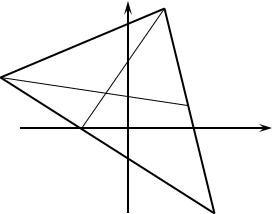
Сделать чертеж (рис.1).
|
|
|
|
|
Решение. 1) Найдем координаты векторов AB и |
AC, для |
|||
|
|
|
|
|
чего воспользуемся формулой AB xb xa; yb ya . |
|
|||
|
|
|
векторы |
являются |
Тогда AB 12; 9 , |
AC 10;5 . Эти |
|||
направляющими |
векторами прямых, |
на которых лежат |
||
соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
x x0 y y0 . l m
В результате получим
x 8 |
|
y 3 |
|
( AB ), |
|||
12 |
|
9 |
|||||
|
|
|
|
||||
x 8 |
|
y 3 |
|
( AC ). |
|||
10 |
|
||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
31 |
|
||

Разрешая эти уравнения относительно y , т.е. приводя их к виду уравнения прямой с угловым коэффициентом
y kx b ,
найдем kAB |
3 |
, |
kAC |
|
1 |
. |
|
|
|||||
4 |
|
|
2 |
|
||
2) Угол A |
|
треугольника совпадает с углом между |
||||
векторами AB и AC, и для его нахождения можно использовать формулу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
cos A |
|
|
AB AC |
, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
AB |
|
AC |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos A |
|
12 10 9 5 |
|
|
|
|
75 |
|
|
|
|
1 |
|
0,4472. По |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(12)2 ( 9)2 (10)2 |
(5)2 |
15 5 5 |
5 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
таблице найдем значение угла A: уголA 1,11 рад. (63 20 ). 3) Для получения уравнения высоты СD приведем
уравнение стороны AB к виду общего уравнения прямой на плоскости
|
|
|
|
|
3x 4y 12 0 ( AB). |
|
|
||||||||||||
|
Из |
рисунка |
видно, |
|
что вектор нормали к прямой |
AB |
|||||||||||||
является |
направляющим вектором высоты CD, |
т.е. |
|||||||||||||||||
n |
AB 3;4 |
a |
CD , |
и |
|
можно |
вновь |
воспользоваться |
|||||||||||
каноническим уравнением прямой на плоскости |
|
||||||||||||||||||
|
|
|
|
|
|
x 2 |
|
|
y 8 |
|
(CD). |
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
|
Длину высоты CD |
|
|
вычислим по формуле вычисления |
|||||||||||||||
расстояния от точки M0(x0,y0) до прямой Ax By C 0: |
|
||||||||||||||||||
|
|
|
|
|
|
d |
|
|
Ax0 By0 |
C |
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
 A2 B2
A2 B2
В нашем случае d CD 3 2 4 8 12 50 10.
(3)2 (4)2 |
5 |
32
4) Найдем координаты точки E, являющейся серединой отрезка BC
xE |
|
xB xC |
|
4 2 |
3; |
yE |
|
yB yC |
|
6 8 |
1. |
|
|
|
|
||||||||
|
2 |
2 |
|
|
2 |
1 |
|
||||
Т.о., E(3,1), и для нахождения уравнения медианы AE можно использовать уравнение прямой, проходящей через две точки
M |
1 |
(x ,y ) и |
M |
2 |
(x |
2 |
,y |
2 |
): |
x x1 |
|
|
y y1 |
. Тогда получим |
|||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
1 1 |
|
|
|
|
|
|
|
x |
2 |
x |
|
|
y |
2 |
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|||
|
|
|
x 3 |
|
y 1 |
|
или |
|
|
|
x 3 |
|
y 1 |
( AE ). |
|||||||||||||
|
|
|
|
|
|
3 1 |
|
|
|
11 |
2 |
||||||||||||||||
|
|
|
8 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Наконец, |
для |
|
вычисления |
|
координат точки K , решим |
||||||||||||||||||||
совместно |
уравнения |
|
прямых |
|
AE и CD, предварительно |
||||||||||||||||||||||
приведя их уравнения к общему виду |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2x 11y 17 0 (AE) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
4x 3y 16 0 (CD) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Отсюда получим |
K |
|
|
,2 |
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
C |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
B
Рис. 1
33
Задача №4
Составить уравнение линии, каждая точка которой одинаково удалена от прямой x 2 и от точки A(4;0) . Сделать чертеж.
Решение. Пусть точка M(x;y) принадлежит искомой линии. Расстояние между точками M1(x1,y1) и M2(x2,y2) вычисляется по формуле
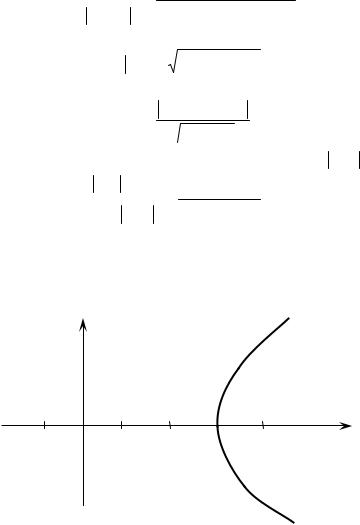
M1M2 
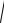 (x2 x1)2 (y2 y1)2 .
(x2 x1)2 (y2 y1)2 .
По условию задачи
AM |
|
|
(x 4)2 y2 |
|
Расстояние от точки M0(x0; y0) до прямой Ax By C 0 d Ax0 By0 C .
 A2 B2
A2 B2
Уравнение прямой x 2 0. Следовательно d x 2 . По условию задачи d AM , т.е.
x 2 
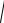 (x 4)2 y2 .
(x 4)2 y2 .
Возведем обе части уравнения в квадрат. Приводя подобные члены, получим 4x y2 12 или y2 4(x 3). Это и есть уравнение искомого геометрического места точек. Следовательно, искомая линия является параболой.
y
y2=4(x-3)
0 |
1 |
2 |
3 |
4 |
x |
|
|
|
|
|
Рис. 2
34

а)
в)
Задача №5
Вычислить пределы, не пользуясь правилом Лопиталя:
lim |
|
5x4 3x |
; |
б) lim |
1 x x2 1 x x |
2 |
; |
||
|
|
|
|
x2 x |
|
||||
x 7x4 2x3 1 |
|
x 0 |
|
|
|||||
lim |
|
x tg 2x |
; |
|
г) lim |
(5 2x)2/(x 2) . |
|
|
|
|
|
|
|
|
|||||
x 0 |
1 cos8x |
|
x 2 |
|
|
|
|||
Решение. а) |
lim |
5x4 3x |
|
. |
|||
|
4 |
2x3 |
1 |
||||
|
x 7x |
|
|||||
И числитель, и знаменатель дроби при x стремятся к бесконечности, т.е. имеем неопределенность вида . Вынося в
числителе |
и |
знаменателе |
|
старшую |
|
|
степень |
|
x4 |
как |
общий |
|||||||||||||||||||||||||||||||||||||||||||
множитель, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
5x4 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x4(5 |
|
) |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
x3 |
|
lim |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|||||||||||||||||||||||||||
|
x 7x4 2x3 1 |
|
x |
x |
|
2 1 |
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7 |
|
|
|
|
|
|
|
) |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x4 |
|
|
|
|
|
|
x |
|
x4 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
lim |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 0 5 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
x3 |
|
|
|
|
|
|
|
x x3 |
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
7 0 |
7 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
7 lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
7 |
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x |
x |
|
|
|
|
x x x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
б) |
|
lim |
|
|
|
1 x x2 |
|
1 x x2 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
И числитель, |
и знаменатель дроби при x 0 стремятся к |
||||||||||||||||||||||||||||||||||||||||||||||||||||
нулю. Имеем неопределенность вида |
|
|
0 . Умножим числитель и |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
знаменатель |
на |
иррационально |
|
|
|
|
сопряженное |
выражение |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1 x x2 |
|
|
1 x x2 |
|
|
а также |
|
|
разложим |
знаменатель на |
|||||||||||||||||||||||||||||||||||||||||||
множители. Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
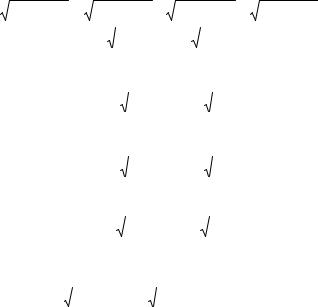
|
lim |
( 1 x x2 1 x x2 ) ( 1 x x2 1 x x2 ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x(x 1) ( 1 x x2 1 x x2 ) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
lim |
|
|
|
1 x x2 1 x x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x 0 x(x 1)( 1 x x2 1 x x2 ) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
2x 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x 0 x(x 1)( 1 x x2 1 x x2 ) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
2(x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x 0 (x 1) ( 1 x x2 1 x x2 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim 2(1 x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
lim (x 1) ( |
1 x x2 |
1 x x2 ) |
|
( 1) (1 1) |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
в) lim |
x tg 2x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 cos8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Имеем неопределенность вида |
|
0 . Воспользуемся первым |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
замечательным |
|
пределом |
lim |
|
sin x |
1 |
|
и |
|
|
|
формулой |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
1 cos2 2sin2 . Получим |
x 0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x tg2x |
|
|
|
|
|
|
x sin2x |
|
|
|
|
|
|
2 |
|
|
sin2x |
|
|
|
|
x2 |
|
|
|||||||||||||||||||||||||
lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 cos8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
sin4x |
|
||||||||||||||||||||||||||||||||
x 0 |
x 0 cos2x 2sin2 4x |
|
|
x 0 cos2x |
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
16x2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x2 |
1 |
|
|
1 |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 16x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 0 cos2x |
|
|
16 x 0 cos2x |
16 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
г) lim |
(5 2x)2/(x 2) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Имеем неопределенность вида 1 . Воспользуемся вторым
замечательным пределом lim |
(1 x)1/ x |
e. |
|
|||
|
x 0 |
|
|
|
|
|
Введем |
в рассмотрение |
новую переменную |
y 4 2x , |
|||
y 0 при |
x 2. Тогда |
x 2 |
y |
. |
Переходя |
к новой |
|
||||||
|
|
2 |
|
|
|
|
переменной, получим
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (5 2x) |
x 2 |
|
lim (1 y)(2 y/2 2 |
lim (1 |
||||||||||
x 2 |
|
|
y 0 |
|
|
|
|
|
|
y 0 |
|
|||
|
|
|
1 |
|
4 |
|
|
|
|
1 |
|
4 |
|
|
(1 y) |
y |
|
|
|
(1 y) |
y |
|
e |
||||||
lim |
|
|
|
lim |
|
|
|
|||||||
y 0 |
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
Задача №6
Найти производные заданных функций.
y) 4y
4 .
а) y |
|
x2 1 |
; |
|
|
б) y (e3x) |
|
|
|
; |
|||||
|
|
|
1 tg x |
||||||||||||
|
sin 2x cos3x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y ln3 |
|
|
|
г) y (x2 1)cos x ; |
||||||||||
в) |
|
arctg (x 2x) |
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
д) |
xy sin(x y); |
|
|
е) |
1 t |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. а) |
y |
|
x2 |
1 |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
sin2x cos 3x
Применяя правило дифференцирования частного двух функций , а также правило дифференцирования сложной функции, получим
37

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
sin 2x cos3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(x |
2 |
1) |
|
(sin2x cos3x) (x |
2 |
1) (sin2x cos3x) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin2x cos3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2x (sin2x |
cos3x) (x |
2 |
|
1)(cos2x (2x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
sin3x (3x) ) |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
sin2x cos3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2x (sin2x cos3x) (x2 1)(2cos2x 3sin3x) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
sin2x cos3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
б) y (e3x) |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Применяя |
|
правило |
|
дифференцирования произведения |
|||||||||||||||||||||||||||||||||||||||||||||
двух функций, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e3x) 1 tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y (e3x) 1 tg x |
|
|
|
(e3x) 1 tg x |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3x(3x) 1 tg x |
(e3x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 tg |
x) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 tg x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
3e3x |
|
|
|
|
e3x |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
1 tg x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 tg x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
e3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 tg x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2cos |
x (1 tg x) |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
в) y ln3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
arctg (x 2x) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Применяя |
|
|
|
правило |
|
|
|
дифференцирования |
|
|
|
сложной |
|||||||||||||||||||||||||||||||||||||
функции, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
3 |
arctg (x 2 |
x |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
ln |
|
|
|
) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3ln |
arctg (x 2 |
x |
|
ln |
arctg (x 2 |
x |
) |
|
|
||||||||||||||||||
|
|
|
|
) |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3ln |
|
arctg (x 2 |
x |
) |
|
|
|
|
|
|
|
|
|
|
|
arctg (x 2 |
x |
) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
arctg (x 2x) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
38
