
Расчет прямоугольной плиты. методические указания к расчетной работе по курсу Прикладная механика. Синозерский А.Н., Резунов А.В
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
РАСЧЕТ ПРЯМОУГОЛЬНОЙ ПЛИТЫ
Методические указания к выполнению расчетной работы и контрольной задачи
для студентов дневной и заочной форм обучения специальности ПГС по курсу "Прикладная механика"
Воронеж 2011
УДК 539.3:624 ББК 30.121
Составители А.Н. Синозерский, А.В. Резунов, Е.И. Осипова
Расчет прямоугольной плиты: метод. указания к расчетной работе и контрольной задаче по курса «Прикладная механика» для студ. дневной и заочной форм обучения спец. ПГС / Воронежский ГАСУ; сост.: А.Н. Синозерский, А.В. Резунов, Е.И. Осипова. – Воронеж, 2010. – 21 с.
Приведены гипотезы и методика исследования перемещений, усилий и напряжений тонких плит. Даются указания по определению прогибов, изгибающих и крутящих моментов, поперечных сил, нормальных и касательных напряжений в прямоугольной плите, пример и решение этой же задачи на ПЭВМ с использованием популярного математического пакета Mathcad.
Предназначены для студентов специальности ПГС дневной и заочной форм обучения.
Ил. 6. Библиогр.: 4 назв.
УДК 539.3:624 ББК 30.121
Печатается по решениюредакционно-издательского совета Воронежского государственного архитектурно-строительного университета
Рецензент – В.Д. Коробкин, доктор. техн. наук, проф. кафедры теоретической механики Воронежского государственного архитектурно-строительного университета
2
ВВЕДЕНИЕ
Приведены гипотезы и методика исследования перемещений, усилий и напряжений тонких плит. Даются указания по определению прогибов, изгибающих и крутящих моментов, поперечных сил, нормальных и касательных напряжений в прямоугольной плите, пример и решение этой же задачи на ПЭВМ с использованием популярного математического пакета Mathcad.
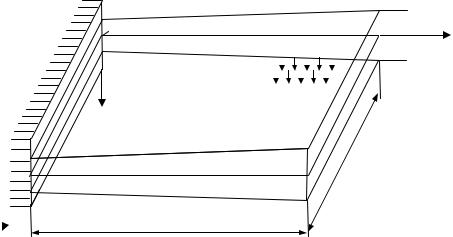
Призматическое или цилиндрическое тело (рис. 1), толщина которого h мала по сравнению с другими габаритными размерами (a, b), называется
пластиной [1,2].
0
q

b
y |
a |
 h/2 h/2
h/2 h/2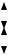
x
Рис. 1
Они применяются в строительстве, авиации, машиностроении, судостроении и т. д. При этом легкость и рациональность форм тонкостенных конструкций сочетаются с их высокой несущей способностью, экономичностью и хорошей технологичностью.
Взависимости от формы основания призмы или цилиндра различают круглые, эллиптические, квадратные, прямоугольные, треугольные и т. п. пластины.
Плоскость, делящая пластину пополам по толщине, называется срединной плоскостью, а линия пересечения её с боковыми гранями – контуром.
Встроительной практике пластины, подвергающиеся изгибу, именуются плитами [3]. Наиболее распространены рассматриваемые в дальнейшем прямоугольные плиты (с прямоугольным контуром и h=const).
3
1. Допущения
Оси x, y декартовой прямоугольной системы координат расположим в срединной плоскости, ось z направим вниз (рис. 1). Материал плиты будем считать сплошным, однородным, изотропным и подчиняющимся закону Гука с модулем упругости E и коэффициентом Пуассона .
Под действием, например, распределенной по площади нагрузки ин-
тенсивности q (кН/м2) точки срединной плоскости получают вертикальные перемещения – прогибы w. Геометрическое место этих точек образует срединную поверхность изогнутой плиты (рис. 2).
Существенное влияние на свойства плиты оказывает толщина h. В дальнейшем рассматриваются только тонкие плиты, для которых выполняются условия
1 |
h |
|
1 |
, |
(1) |
|
80 |
5 |
|||||
r |
|
|
|
|||
max w h |
, |
(2) |
||||
|
|
|
4 |
|
|
|
где r – наименьший габаритный размер, max w – наибольший прогиб.
Помимо изложенных выше ограничений теория расчета тонких плит основана на трех гипотезах (допущениях).
|
0 |
Срединная плоскость |
|
||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
c |
|
|
w |
|
z |
. |
|
h/2 |
|
d |
c1 |
|
||
|
|
w |
. |
|
|
|
|
|
d1 |
h |
b |
|
|
|
|
||
Срединная поверхность 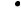
y
a
Рис. 2
Кинематическая гипотеза: любой линейный элемент (cd на рис. 2), нормальный к срединной плоскости, остаётся прямолинейным и перпендику-
4
лярным к срединной поверхности и длина его не изменяется (c1d1=cd=h). Следовательно, отсутствуют угловые и линейные в направлении оси z деформации
xz yz 0, |
(3) |
z 0. |
(4) |
Так как z w / z, то прогиб является функцией только двух переменных
w=w(x,y). |
(5) |
Статическая гипотеза: давлением горизонтальных слоёв плиты друг на друга можно пренебречь, полагая
z 0. |
(6) |
Тогда в соответствии с обобщённым законом Гука линейные деформации по осям x, y будут определяться по формулам
|
x |
( |
x |
|
y |
) / E, |
|
|
|
|
|
(7) |
|||
|
|
|
|
|
|
|
|
y ( y x ) / E. |
|
||||||
|
|
|
|
|
|
|
|
Гипотеза о недеформируемости срединной плоскости: деформации растяжения, сжатия ( x , y ) и сдвига ( xy ) в срединной плоскости отсутствуют, а следовательно она является нейтральной. Для точек срединной плоскости перемещения по осям x, y равны нулю
u0 v0 0. |
(8) |
На видимых гранях элемента (рис. 3) плиты размерами x y 1 и толщиной h показаны напряжения и погонные (приходящиеся на единицу длины плиты) внутренние усилия, которые следует учитывать при расчёте тонких плит.
5

|
|
x=1 |
|
0 |
|
y=1 |
|
Mxy |
|
|
|
|
z |
|
|
Myx |
Qxz |
|
|
σx |
|
|
τyx |
|
Qyz |
τxyτxz |
Myy |
τyz |
|
y |
σy |
|
x
z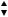 h/2
h/2
dz Mxx
Рис. 3
x , y – нормальные напряжения, xy , yx – касательные напряжения; Qxz , Qyz – внутренние погонные поперечные силы;
Mxy , Myx – внутренние погонные изгибающие моменты; Mxx , Myy – внутренние погонные крутящие моменты
2. Методика расчета
Решение задачи по определению перемещений, деформаций, усилий и напряжений обычно выполняют в перемещениях. За основную неизвестную
принимают функцию прогибов w=w(x,y) [1,2].
Рассматривая условия для сдвигов (3), из соотношений Коши с учётом
(8) получают перемещения
u z wx ,
w (9) v z y .
Подставляя в зависимости Коши перемещения (9), находят отличные от нуля деформации
|
|
|
u |
z |
|
2 |
w |
, |
|
|
|
||
x |
|
|
|
|
|||||||||
|
|
x |
|
|
|
x2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
v |
z |
w |
, |
|
(10) |
|||||
y |
|
|
|||||||||||
|
|
y |
|
|
|
y2 |
|
|
|
|
|||
|
|
|
u |
|
v |
|
|
|
|
2w |
|
|
|
|
xy |
|
|
|
|
|
2 z |
|
. |
|
|||
y |
|
x |
x y |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
Далее с помощью закона Гука в обратной форме с учётом равенства (6) получают напряжения x , y , xy в виде функций упругих постоянных E,
и прогиба w(x,y). Пренебрегая объёмными силами и учитывая отсутствие касательных нагрузок на верхней и нижней поверхностях плиты, из дифферен-
циальных уравнений равновесия устанавливают зависимости xz , yz от E, ,
w(x,y), h.
Рассматривая элементарные внутренние усилия, действующие на площадке толщиной dz и единичной ширины (рис. 3), и интегрируя эти усилия по толщине плиты, приходят к следующим выражениям для погонных
изгибающих моментов: |
Mxy |
|
|
|
2 |
w2 |
|
2 |
w2 |
|
, |
|
|
|
||||
D |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
y |
|
|
|
|
(11) |
|||||
|
|
|
|
|
|
2 |
w2 |
|
2 |
w2 |
|
|
|
|
||||
|
Myx |
|
|
|
; |
|
|
|
||||||||||
|
D |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|||||
крутящих моментов: |
Mxx Myy D 1 |
2w |
; |
(12) |
||||||||||||||
x y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
поперечных сил: Qxz D |
|
|
2 w |
, Qyz D |
|
2 w , |
(13) |
|||||||||||
x |
y |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где D – цилиндрическая жёсткость плиты: |
|
|
|
|
|
|
|
|
|
|||||||||
|
D |
|
|
E h3 |
|
; |
|
|
|
|
|
|
|
|
(14) |
|||
|
|
12 1 2 |
|
|
|
|
|
|
|
|
||||||||
|
2w |
2 w |
2 w |
; |
|
|
|
|
|
|
|
(15) |
||||||
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|||
E и – модуль упругости и коэффициент Пуассона, h – толщина плиты. Выражения для напряжений через внутренние усилия (11)–(13) имеют
следующий вид:
x |
12 Mxy z |
|
, y |
12 Myx z |
; |
||||||||||||||||||
|
h3 |
|
|
|
|
h3 |
|
|
|||||||||||||||
xy |
12 Mxx z |
|
, yx |
12 Myy z |
; |
||||||||||||||||||
|
h3 |
|
|
|
|
|
h3 |
|
|
||||||||||||||
|
|
|
12 Q |
xz |
S |
|
|
|
|
|
|
12 Q |
yz |
S |
|||||||||
|
xz |
|
|
|
|
y |
, |
|
yz |
|
|
|
|
|
|
x |
, |
||||||
|
|
h3 |
|
|
|
|
h3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
1 |
|
h2 |
z |
2 |
|
|
|
|
|
|||||
|
|
|
|
Sy |
Sx |
2 |
|
4 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- статический момент |
части |
|
сечения |
высотой |
|||||||||||||||||||
x y 1 (рис. 4,в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(16)
(17)
(18)
(19)
0.5 h z и шириной
7
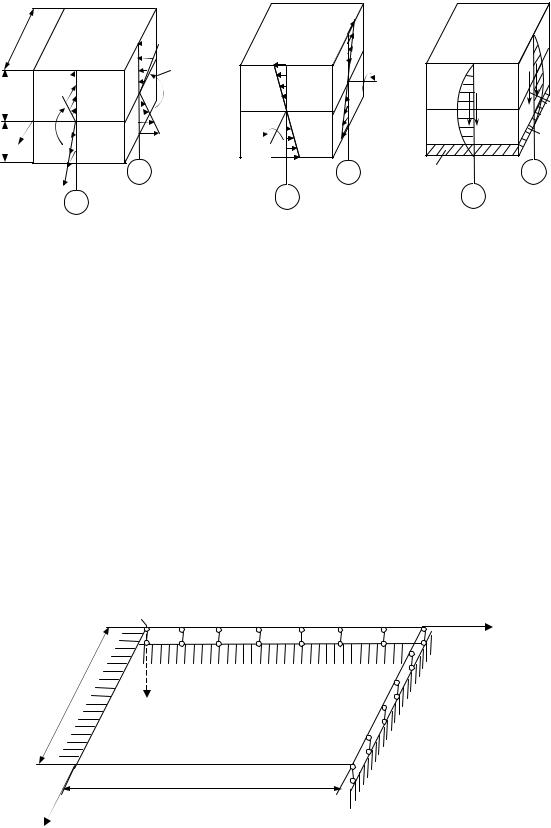
Эпюры нормальных x , y , касательных xy , yx и xz , yz напряжений представлены на рис. 4, а, б и в.
y=1 |
|
|
|
|
|
|
Mxy |
|
Mxx |
|
|
h/2 |
Myx |
|
|
|
Qxz |
|
|
|
|
||
h/2 |
|
|
|
Qyz |
ω |
|
|
|
|
||
y |
|
|
|
|
|
|
σx |
τxy |
ω |
|
τxy |
|
σy |
τyz |
|
τyz |
|
|
а) |
б) |
|
в) |
|
Рис. 4
Рассматривая равновесие элемента плиты размерами в плане dx, dy под действием распределённой нагрузки q после преобразований придём, к диф-
ференциальному уравнению срединной поверхности плиты
4w |
2 |
|
4 w |
|
4w |
|
q |
. |
(20) |
||
x4 |
x2 |
y4 |
y4 |
D |
|||||||
|
|
|
|
|
|
||||||
Уравнение (20) называется разрешающим, а функция прогибов w(x,y), которая удовлетворяет уравнению (20) и условиям на контуре плиты, – раз-
решающей функцией.
Сформулируем граничные условия для различных случаев закрепления контура прямоугольной плиты (рис. 5).
y=0 |
x |
b |
|
z |
x=a |
x=0 |
y=b
a
y
Рис. 5
8
Защемленный край (геометрические условия): при x=0 невозможны прогиб и поворот сечения относительно оси x, т. е. заданы перемещения
w(0,y) 0 и w(0,y)/ x 0. |
(21) |
Свободный край (статические условия): при y=b=const отсутствуют |
|
поперечная сила Qyz , крутящий Mxx и изгибающий Myx |
моменты, т. е. зада- |
ны усилия. Вместо необходимых двух имеем три условия, что объясняется приближенностью используемых при решении допущений. Противоречие устраняют, заменив первые два условия требованием равенства нулю обобщённой поперечной силы. В итоге на свободном крае получают следующие условия:
3w x,b |
|
2 |
|
3w x,b |
|
|
||||
|
|
|
|
|
|
|
0, |
|
||
y |
3 |
|
x |
2 |
y |
|
||||
|
|
|
|
|
|
|
(22) |
|||
2w x,b |
|
|
2w x,b |
|
|
|||||
|
|
0. |
|
|
||||||
y |
2 |
|
x |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Шарнирно опёртые края (смешанные условия): при y=0 или x=a=const прогибы и изгибающие моменты Myx или Mxy равны нулю, т. е.
заданы часть перемещений и усилий. Линии y и x a остаются неизо-
гнутыми, поэтому w(x,0) / x 2 w(x,0) / x2 0
и w(a, y) / y 2 w(a, y) / y2 0, что с учётом (11) приводит к соотношениям
w(x,0) 0 |
и 2w(x,0)/ y2 |
0, |
|
|||
или |
|
|
|
|
|
(23) |
|
|
|
|
|
||
w(a,y) 0 |
и |
2 |
w(a,y)/ x |
2 |
|
|
|
|
0. |
|
|||
После того как функция прогибов w(x, y) будет найдена (удовлетворя-
ет уравнению (20) и граничным условиям) все остальные величины вычис-
ляют из выражений (9) – (13) и (16) – (19).
3. Задание
Объектом исследования является нагруженная по верхней поверхности равномерно распределённой поперечной нагрузкой интенсивностью q прямоугольная в плане, шарнирно опёртая по контуру плита со сторонами a, b и толщинойh (рис. 6), модулемупругостиE икоэффициентомПуассонаνматериала.
9

q
0
a
z
yA
xA
 A
A
y
h/2 |
|
|
h/2 |
x |
|
h |
||
|
||
|
x |
|
b |
q |
|
|
Рис.6. М.1:35
Разрешающую функцию принять в виде двойного тригонометрического ряда:
|
|
sin n y . |
|
w(x, y) Amn sin m x |
(24) |
||
m 1 n 1 |
a |
b |
|
В этом случае условия на контуре (23) удовлетворяются, а дифференциальное уравнение (20) обращается в тождество, если коэффициенты ряда будут равны
|
|
|
4 |
|
|
|
|
|
|
b a |
|
|
|
Amn |
|
|
|
|
|
|
|
|
q(x, y) sin m x |
sin n y |
dy dx, |
||
|
|
m2 |
n2 |
|
2 |
||||||||
|
D |
4 |
|
0 0 |
a |
b |
(25) |
||||||
|
|
a b |
a |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где m 1,2,3 ; n 1,2,3 и т. д.
10
