
Физико-химические проблемы и высокие технологии строительного материаловедения. Рудаков О.Б., Борисов Ю.М
.pdf
ISSN 2225-1995
НАУЧНЫЙ ВЕСТНИК
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ
АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ
УНИВЕРСИТЕТ
Серия:
Физико-химические проблемы и высокие технологии
строительного материаловедения
•МАТЕРИАЛОВЕДЕНИЕ. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ
•ТЕХНОЛОГИЯ СТРОИТЕЛЬНЫХ ИЗДЕЛИЙ И КОНСТРУКЦИЙ
•ФИЗИЧЕСКАЯ ХИМИЯ СТРОИТЕЛЬНЫХ И ТЕХНИЧЕСКИХ МАТЕРИАЛОВ
•МЕТОДЫ КОНТРОЛЯ И ДИАГНОСТИКИ МАТЕРИАЛОВ И ИЗДЕЛИЙ
•ПОЖАРНАЯ И АВАРИЙНАЯ БЕЗОПАСНОСТЬ
•ХРОНИКА, БИБЛИОГРАФИЯ
Выпуск № 6
2013 г
Научный Вестник Воронежского государственного архитектурно-строительного университета
УДК 54 |
ISSN 2225-1995 |
ББК 24 |
|
ФИЗИКО-ХИМИЧЕСКИЕ ПРОБЛЕМЫ И ВЫСОКИЕ ТЕХНОЛОГИИ СТРОИТЕЛЬНОГО МАТЕРИАЛОВЕДЕНИЯ
Редакционный совет научного журнала
Главный редактор д-р. хим. наук, проф. О.Б. Рудаков; д-р. техн. наук, проф. Ю.М. Борисов; зам. главного редактора д-р. хим. наук, проф. Г.В. Славинская; зам. главного редактора д-р. техн. наук проф. В.Т. Перцев.
Редакционная коллегия научного журнала
Д-р техн. наук, проф. В.В. Белов (г. Тверь, ТвГТУ); д-р техн. наук, проф. А.Н. Бобрышев (г. Пенза, ПГУАС); к.т.н., проф. В.В. Власов (г. Воронеж, Воронежский ГАСУ); д-р техн. наук, проф. Гаркави М.С. (г. Магнитогорск, МГТУ им. Г.И. Носова); д-р техн. наук, проф. С.С. Глазков (г. Воронеж, Воронежский ГАСУ); д-р физ.-мат. наук, проф. П.А. Головинский (г. Воронеж, Воронежский ГАСУ); д-р техн. наук, профессор Ю.Г. Иващенко (г. Саратов, СГТУ им. Ю.А. Гагарина); д-р хим. наук, проф. А.В. Калач (г. Воронеж, ВИ ГПС МЧС России); д-р техн. наук, проф. В.И. Калашников (г. Пенза, ПГУАС); д-р техн. наук, проф. А.Д. Корнеев (г. Липецк, ЛГТУ);д-р техн. наук, проф. Л.В. Моргун (г. Ростов, РГСУ); д-р техн. наук, проф. Ю.В. Пухаренко (г. Санкт-Петербург, СПбГАСУ); д-р техн. наук, проф. Ш.М. Рахимбаев (г. Белгород, БГТУ им. В.Г. Шухова); д-р хим. наук, проф. В.Ф. Строганов (г. Казань, КГАСУ); д-р техн. наук, проф. И.С. Суровцев (г. Воронеж, Воронежский ГАСУ); д-р техн. наук, проф. А.А. Трещев (г. Тула, ТулГТУ); д.-р. техн. наук, проф. Е.М. Чернышов (г. Воронеж, Воронежский ГАСУ); д-р физ.-мат. наук, проф. М.В. Шитикова (г. Воронеж, Воронежский ГАСУ); д-р техн. наук, проф. В.П. Ярцев (г. Тамбов, ТГГУ).
Секретарь выпуска - канд. физ.-мат. наук, ст. преподаватель Никишина А.И. (г. Воронеж, Воронежский ГАСУ.)
Технический редактор выпуска - м.н.с. департамента науки и инноваций Альбинская Ю.С. (г. Воронеж, Воронежский ГАСУ)
В вестнике данной серии публикуются результаты научных исследований и производственного опыта сотрудников университета и других вузов страны по проблемам физической химии строительных и технических материалов; химической технологии и физико-химическим методам контроля качества строительных и других технических материалов, применяющихся в строительстве; по экологии и химической безопасности строительных технологий и др.
Опубликованные материалы могут быть полезны специалистам в области производства строительных работ, эксплуатации зданий и сооружений и других конструкций, а также исследователям при разработке новых технологий получения строительных и отделочных материалов, при осуществлении контроля их технологических свойств новыми методами; инженерно-техническим работникам, интересующимся вопросами экологии гидросферы, атмосферы и литосферы; специалистам других направлений - научным сотрудникам, преподавателям, аспирантам, магистрантам и студентам строительных и других образовательных учреждений.
АДРЕС РЕДАКЦИИ 394006 г. Воронеж, ул. 20-летия Октября, 84, ком. 6418
тел.: (473) 2369350, (473)2717617 E-mail: chemistry@vgasu.vrn.ru
Воронежский государственный архитектурно-строительный университет
Перепечатка материалов журнала допускается только с разрешения редакции
2

Научный Вестник Воронежского государственного архитектурно-строительного университета
МАТЕРИАЛОВЕДЕНИЕ. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ
УДК 235. 016
П.А. Головинский, М.А. Преображенский
ЗАМКНУТЫЕ ВЫРАЖЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ ОТРАЖЕНИЯ И ПОГЛОЩЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ОТ ПОВЕРХНОСТИ МЕТАЛЛА
Получены точные выражения для коэффициентов отражения и преломления волн электромагнитных волн на границе раздела двух сред, одна из которых является прозрачным диэлектриком, а вторая имеет комплексный коэффициент преломления. Аналитические результаты проиллюстированы конкретными примерами. Найденные соотношения могут быть использованы при решении задач о спонтанном излучении атомов и наночастиц вблизи границы раздела диэлектрик-металл, а также при решении задач классической электродинамики.
Ключевые слова: коэффициент отражения, коэффициент преломления, металл, диэлектрик, комплексный показатель преломления
P.A. Golovinsky, M.A. Preobrazhensky
THE CLOSED EXPRESSIONS FOR
REFLECTIONS AND ABSORPTION FACTORS OF
THE ELECTROMAGNETIC WAVE FROM A METAL SURFACE
Exact expressions have been received for the reflection and refraction factors of electromagnetic waves on the interface of two media, one of which is transparent dielectric, while the second medium has complex factor of refraction. Analytical results have been illustrated by specific example. The found relationships could be used for solving the problems on spontaneous radiation of atoms and nanoparticles near the interface dielectric-metal, as well as for the solution of problems of classical electrodynamics.
Keywords: factor of reflection, factor of refraction, metal, dielectric, complex indicator of refraction
Введение. В настоящее время значительные экспериментальные и теоретические усилия направлены на исследование электродинамики наноструктур [1]. Значительную роль в соответствующих процессах играют плазмонные эффекты [2], которые качественно меняют характер взаимодействия наночистиц электромагнитным полем, особенно на малых расстояниях. При этом оказываются востребованы и соотношения классической электродинамики, которых, например, невозможно построить функции электромагнитного поля при наличии близких диэлектрических или металлических поверхностей. В связи с этим требуются точные соотношения для отражения и преломления электромагнитных волн на границе раздела сред. Классическая теория для случая плоского раздела между двумя прозрачными диэлектриками хорошо известна [3]. Ряд современных результатов, относящихся к оптике металлов, отражен в [4-6], в то время как более раннее состояние вопроса можно изучить по работе [7]. Данная работа посвящена систематизации имеющихся результатов для задачи отражения электромагнитных волн от границы раздела двух сред, одна из которых является прозрачным диэлектриком, а другая характеризуется комплексным показателем преломления, что позволяет единым образом включить в описание в качестве второй среды и металлы.
Общие соотношения. Общие выражения, связывающие комплексные амплитуды падающей, отраженной и преломленной плоских волн на границе раздела изотропных сред
© Головинский П.А., 2013
3
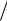
Научный Вестник Воронежского государственного архитектурно-строительного университета
были получены Френелем на основе теории, рассматривающей свет как колебания упругой среды, в виде [8]:
R |
|
|
n2 cos i n1 cos t |
A |
; |
R |
|
|
n1 cos i n2 cos t |
A |
. |
. |
(1) |
|| |
|
|
|||||||||||
|
|
n2 cos i n1 cos t |
|| |
|
|
|
n1 cos i n2 cos t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь A – |
вектор, характеризующий |
падающую волну, n1,n2 |
– |
показатели |
|||||||||
преломления сред, i , t – углы падения и преломления соответственно. Индексы амплитуд
отражают поляризацию волн – параллельную и перпендикулярную плоскости падения соответственно. При этом, однако, поскольку коэффициенты преломления могут принимать комплексные значения, амплитуды R не являются наблюдаемыми величинами. Определить непосредственно наблюдаемые параметры можно, выделяя в уравнениях (1) действительные и мнимые части в виде
|
R|| || exp i || A||; |
|
R exp i A , |
|
(2) |
|||
В частности, если падающая волна линейно поляризована, то модули и фазы |
||||||||
комплексного |
коэффициента отражения |
||, ||, , определяют |
параметры эллипса |
|||||
поляризации отраженной волны. При этом |
отношение |
модулей |
| | |
|
определяет |
|||
эксцентриситет, а разность || – ориентацию его осей [8]. |
|
|
|
|
||||
Амплитуды и фазы комплексных коэффициентов отражения |
получены только для |
|||||||
частных случаев нормального и скользящего |
падения [8]. |
В |
работе |
[9] |
приведены |
|||
алгебраические |
уравнения, позволяющие |
рассчитать величины |
||, ||, |
, . Однако |
||||
замкнутые выражения для них до сих пор получены не были. Получение этих выражения и является целью данной работы.
Вследствие скин-эффекта глубина проникновения электромагнитных волн в металлы мала во всех диапазонах. Так, в видимом диапазоне она составляет несколько нанометров, а в диапазоне длинных радиоволн – несколько миллиметров. Поэтому граничные условия для проходящих волн мы в данной работе исследовать не будем.
Рассмотрим падение волны из вакуума ( n1 1 ) на металл ( n2 n 1 i ) (здесь n и– действительная часть показателя преломления металла и коэффициент поглощения
соответственно). Пусть плоскость падения совпадает с |
координатной |
плоскостью z0x |
||
(рис.1). Тогда составляющие электрического вектора E падающей и отраженной волн могут |
||||
быть представлены в виде A 0, Ay ,0 , A|| Ax ,0, Az |
и R 0, Ry ,0 , R|| Rx ,0, Rz . |
|||
При этом, компоненты вектора A колеблются синфазно, |
а вектора R ‒ |
с разностью фаз, |
||
равной || . |
|
|
||
Закон преломления принимает вид |
|
|
||
|
sin i |
n 1 i . |
(3) |
|
|
|
|||
|
sin t |
|
|
|
Соотношение (3) позволяет выразить cos t через cos i в виде
4
Научный Вестник Воронежского государственного архитектурно-строительного университета |
|||||||
cos t |
n2 1 2 2 sin 2 |
i |
1 2 2i |
C cos i sin |
|
||
n 1 2 |
|
|
(4) |
||||
|
|
|
|
||||
|
E |
|
|
z |
E |
|
|
E|| |
k |
Θi |
|
E|| |
|
||
|
Θi |
k |
|
||||
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
Металл |
|
|
|
|||
Рис.1. Относительное расположение векторов напряженности электрического и магнитного полей |
|
||||||
и импульса электромагнитной волны при отражении от поверхности металла. Напряженность |
|
||||||
магнитного поля перпендикулярна плоскости чертежа и направлена к наблюдателю |
|
||||||
Модуль cos t имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
n2 |
1 2 2 |
1 |
2 sin 2 |
i |
2 |
4 2 sin 4 |
i |
14 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Фаза |
cos t определяется выражением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
1 |
arctg |
|
|
|
|
|
|
|
|
|
2 sin 2 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||||||||
|
|
|
|
2 |
n |
2 |
1 |
2 2 |
|
|
|
|
2 |
i 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Поскольку |
cos arctg x |
|
1 |
|
|
|
|
|
и |
справедливы |
|
соотношения для |
функции |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
половинного угла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
1 cos arctgx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 cos arctgx |
|
|
|||||||||||||||||||||||||||
cos |
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
, sin |
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 x2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 x2 1 |
|
|
|||||||||||||||||||||||
|
|
cos |
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
; sin |
|
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
. |
(7) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 1 x2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 1 |
x2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

Научный Вестник Воронежского государственного архитектурно-строительного университета
Подставляя выражения (5), (6),(7) в формулу (4), получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
i |
|
|
|
|
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
1 |
1 |
|
(8) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
4 1 2 4 |
|
2n2 sin 2 |
1 4 |
sin 4 |
1 2 2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
(9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 1 2 2 |
sin 2 |
|
1 2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, комплексная функция cos t может быть выражена в виде |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
C iC , |
|
|
|
|
|
|
|
|
|
|
(10) |
||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
C C |
|
|
K 1 |
|
|
|
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставляя выражение (10) в уравнения (1) и учитывая соотношение n2 n 1 i , |
|||||||||||||||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
n 1 i cos i C iC |
|
|
A |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|| |
|
|
|
n 1 i cos i |
C iC |
|
|
|
|
|| |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos i |
n 1 i C iC |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
A |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos i |
n 1 i C iC |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому модули коэффициентов отражения имеют вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|| |
|
|
|
n cos i |
C 2 |
n cos i |
C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
n cos i |
C 2 |
n cos i |
C 2 |
|
|
|
|
|
|
|
|
|
|
(13) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
cos i |
n C C 2 |
n2 C C 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
cos i |
n C C 2 |
n2 C C 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Для вычисления фаз отраженных волн поляризованных в плоскости падения |
|||||||||||||||||||||||||||||||||||||||||||||||
представим уравнения (12) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
R|| |
|
n 1 i cos i C iC n 1 i cos i C iC |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 i cos |
|
C |
|
iC |
|
|
|
|
2 |
|
|
|
(14) |
||||||||||||||||||||
|
A|| |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, фаза коэффициента отражения волны поляризованной в плоскости падения определяется отношением мнимой и действительной части числителя выражения (14):
6
Научный Вестник Воронежского государственного архитектурно-строительного университета
|
|
|
|
|
2n cos |
i |
C C |
|
|
|
|
|
|
|
|
||||
|
|
|
|| arctg |
|
|
|
|
|
|
|
|
|
|
|
|
(15) |
|||
|
|
|
n2 cos2 i |
2 1 C2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Аналогично, поскольку в соответствии с уравнением (12) справедливо равенство |
|
||||||||||||||||||
|
R |
|
cos i n 1 i C iC cos i |
n 1 i C iC |
, |
(16) |
|||||||||||||
|
A . |
|
cos |
i |
n 1 |
i C |
|
iC |
|
|
|
2 |
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то фаза коэффициента отражения волны поляризованной перпендикулярно плоскости падения определяется соотношением
|
2n cos |
C C |
|
|
|
|
arctg |
i |
|
|
|
|
|
n2 1 2 C2 cos2 |
i |
|
(17) |
|||
|
|
|
|
|
|
|
Комплексный коэффициент поглощения |
железа |
волны с |
длиной |
589.3 нм |
||
(желтая линия натрия) равен n2 1.51 1.63i . [8]. |
Модули |
и фазы |
коэффициентов |
|||
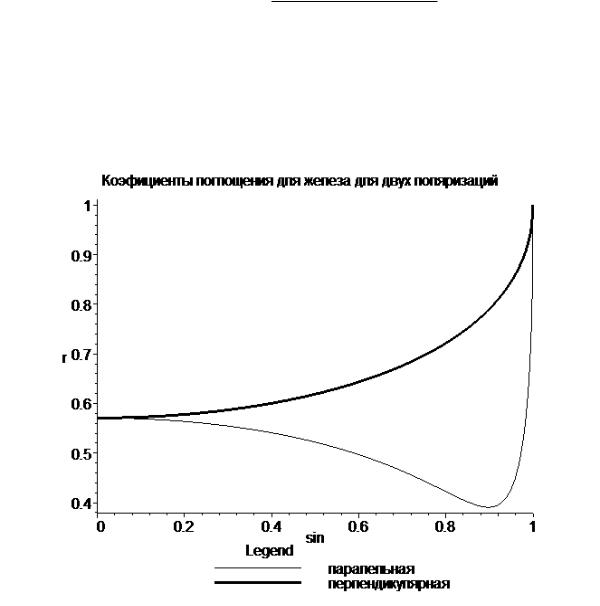
поглощения железом волн различных поляризаций для указанной длины волны приведена на рисунках 2 и 3. На обоих графиках жирная линия соответствует волне поляризованной в плоскости падения, тонкая – плоскости перпендикулярной плоскости падения.
Рис. 2. Зависимость модулей коэффициентов поглощения железом света с длиной волны 589.3 нм от синуса угла падения для двух поляризаций падающего излучения
7
Научный Вестник Воронежского государственного архитектурно-строительного университета
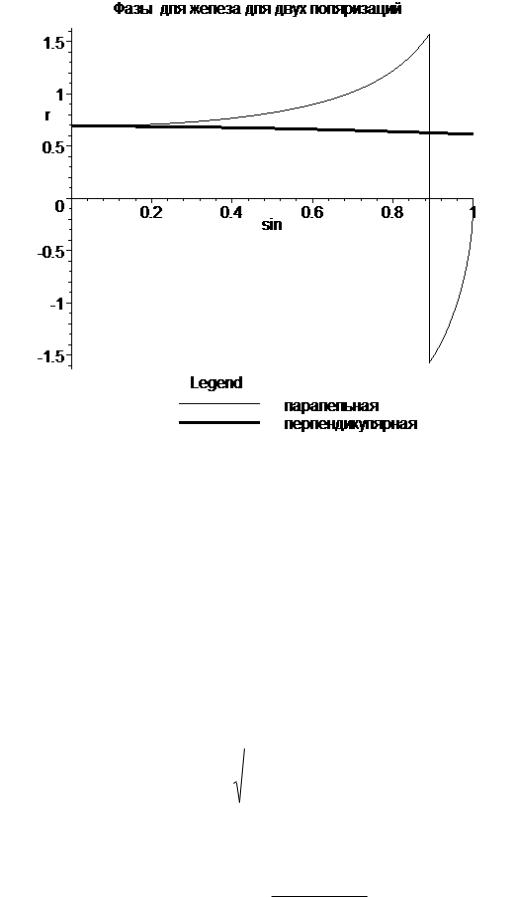
Рис. 3. Зависимость фаз коэффициентов поглощения железом света с длиной волны 589.3 нм от синуса угла падения для двух поляризаций падающего излучения.
Скачок фазы || соответствует главному углу падения, для которого, как показано в
[8], линейно поляризованное излучение, в общем случае после отражения превращается в эллиптически поляризованное. При этом оси эллипса поляризации параллельны и перпендикулярны плоскости падения соответственно.
Частные и предельные случаи общих соотношений. Нормальное падение: i 0.
В этом случае в соответствии с равенством (3) sin i sin t 0 и, следовательно, вне зависимости значений коэффициентов преломления и поглощения должны выполнятся
равенства C 1, |
C 0 . Выполнение этих условий возможно при значениях C K 1 |
|||||
, что соответствует равенствам (5) и (11) |
при sin i 0. При этом, вне зависимости от |
|||||
поляризации волны, модули коэффициентов отражения определяются равенством |
|
|||||
|
|
|
|
|
|
|
|
|| |
n 1 2 n2 2 |
, |
|
(18) |
|
|
n 1 2 n2 2 |
|
||||
|
|
|
|
|
||
что совпадает с результатами [8]. Фазы |
равенством коэффициентов отражения |
при |
||||
cos i 1 принимают вид |
|
|
|
|
|
|
|
|| arctg |
2n |
|
|
|
|
|
n2 1 2 1 |
|
(19) |
|||
|
|
8 |
|
|
|
|
Научный Вестник Воронежского государственного архитектурно-строительного университета
Поскольку |
выполняется равенство || , то отраженный свет остается плоско |
поляризованным, и направления поляризации падающего и отраженного света совпадают.
Скользящее падение: i 2 . В этом случае cos i |
0. При этом выражения (5) и |
||||||||||||||||||||||||||||||
(9) упрощаются и принимают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n2 |
1 2 2 1 2 2 4 |
2 14 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(20) |
||
|
|
|
|
|
|
|
|
|
n 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n4 1 2 4 2n2 1 4 1 2 2 |
(21) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
n2 1 2 |
2 1 2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
При этом, в соответствии с равенствами |
(15) и (17) || |
0 и |
в соответствии с |
||||||||||||||||||||||||||||
равенствами (13) |
|| 1 , что совпадает с результатом работы [1, § 13.2]. |
||||||||||||||||||||||||||||||
Отражение от диэлектрика.В этом случае 0 и выражения (5) и (9) значительно |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
упрощаются и |
принимают вид C |
|
|
|
n2 |
sin 2 |
i |
; |
|
|
|
|
K 1, вследствие чего, в силу |
||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
равенства (11), величины C |
принимают следующие значения C С, |
C 0 . Поэтому |
|||||||||||||||||||||||||||||
формулы (13) в этом частном случае принимают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|| |
|
n2 cos |
i |
|
|
n2 sin |
2 |
i |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n2 cos |
i |
|
|
n2 sin |
2 |
i |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
i |
|
|
n2 sin 2 |
i |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
cos |
|
|
|
|
n2 sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
с точностью до обозначений, совпадающих с формулами Френеля для диэлектрика [1, 8]. Числители выражений, определяющих фазы отраженных лучей (равенства (15) и
(17)) стремятся к нулю в пределе малых коэффициентов поглощения. При этом, для угла
|
|
|
1 |
|
|
|
Брюстера cos |
i |
|
|
|
к нулевому пределу стремятся и знаменатель выражений (15). |
|
|
||||||
|
|
|
n2 1 |
|
||
|
|
|
|
|||
Поэтому фаза коэффициента отражения луча, поляризованного в плоскости падения, в этом случае не определена, а амплитуда – равна нулю.
Отражение от металла. Приведем теперь результаты расчетов коэффициента отражения в широком диапазоне изменения действительной и мнимой части показателя
преломления |
для оптических частот. Согласно данным [7] |
в оптическом диапазоне |
||
действительная часть показателя преломления лежит в диапазоне от |
n 0.031(для натрия) |
|||
до n 4.15 (для галлия). Мнимая часть лежит в диапазоне от 1 |
(для железа) до 61 |
|||
(для натрия). |
При этом в любом случае |
n2 2 3. Графики зависимости модулей и |
||
амплитуд коэффициента поглощения от |
действительной и |
мнимой части показателя |
||
|
|
9 |
|
|
Научный Вестник Воронежского государственного архитектурно-строительного университета
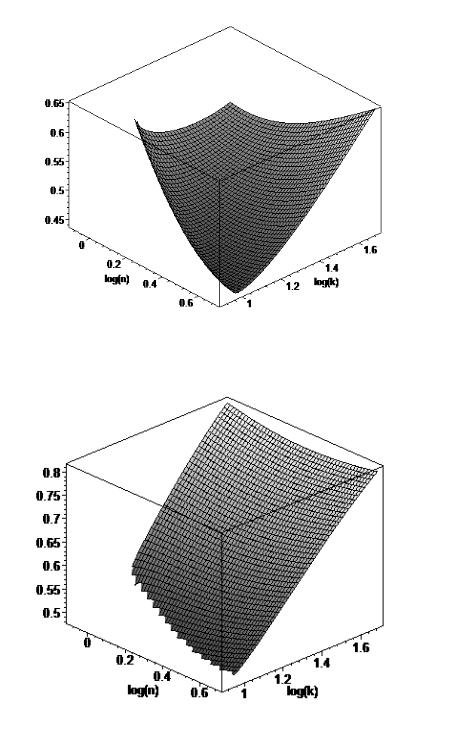
преломления, лежащих в указанном диапазоне, при фиксированном значении угла паденияi 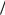 6приведены на рисунках 3 – 6. На всех рисунках масштаб по осям абсцисс и ординат
6приведены на рисунках 3 – 6. На всех рисунках масштаб по осям абсцисс и ординат
логарифмический, по оси аппликат – линейный. Вид зависимости для других углов падения качественно не изменяется. Фаза для всех металлов остается практически постоянной вне зависимости от значений n, и здесь не приводится.
Рис. 4. Зависимость || от действительной и мнимой части коэффициента преломления металла
Рис. 5. Зависимость от действительной и мнимой части коэффициента преломления металла
10
