Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 644

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

				2x2
			x2
7)	x1		x2
7)	x		3x
	x		3x
		1			2
	4x
		1
	x1		x2
				4x2
9)				4x2
9)
	3x1
	2x				x	2
		1				2

3x3 x4 1,

2x3 x4 1,

5x3		0,
	4x4	3.
x3	x4	3,

3x3 x4 1,

x3 x4 2,

3x3 2x4 0.

			x1	2x2 x3												4,
				2x2 x3 x4 2,
11)				2x2 x3 x4 2,
11)		3x x							x x							1,
		3x x					2		x x			4				1,
				1			2			3		4
			x1 3x2 x3 x4 5.
			x1 3x2 x3 x4 5.
				4x2 5x3						x4 0,
																	1,
13)	x1 7x2 3x3																1,
13)			x 3x 5x 3x 0,
			x 3x 5x 3x 0,
			1	2					3			4
				x2 3x3							x4 4.
				x2 3x3							x4 4.
				x2 2x3 3x4 0,
			x1	x2 3x3													1,
15)			x1	x2 3x3													1,
15)			x	x							x						2,
			x	x	2						x		4				2,
			1		2								4
	2x x				2			x		4x					4		0.
			1		2				3						4
	2x1			x2 4x3													1,
				x2					x3 x4 2,
17)				x2					x3 x4 2,
17)			2x	2x					3x		x						0,
			2x	2x		2			3x		x			4			0,
			1			2				3				4
			x	x					x								0.
			1		2					3

					2x2 3x3 4x4 2,
													x3 2x4 1,
8)	2x1												x3 2x4 1,
8)	2x				2x								4x			2x											3,
	2x				2x					2			4x			2x									4		3,
			1							2				3											4
	2x 2x									2			2x						6x						4		1.
			1							2				3											4
	3x1 2x2 3x3																						4,
													x3 x4 1,
10)	2x1												x3 x4 1,
10)		5x		2x								4x												0,
		5x		2x					2			4x												0,
			1						2					3
	3x			2x					2			3x				x					4				1.
			1						2					3							4
	2x1				x2												x4 2,
							x2 2x3 x4 0,
12)							x2 2x3 x4 0,
12)	2x				2x								3x														2,
	2x				2x					2			3x														2,
			1							2				3
	2x											3x 2x												4			2.
			1											3										4
					x2 x3									3x4 3,
								x3						x4 1,
14)	x1							x3						x4 1,
14)	x x													4x								2,
	x x					2								4x					4			2,
			1			2													4
	x x					2		2x 2x											4			4.
			1			2							3						4
					x2 x3 3x4 3,
										x3 x4 1,
16)	x1									x3 x4 1,
16)	x			x										4x							2,
	x			x			2							4x				4			2,
			1				2											4
	x x						2	2x 2x												4			4.
			1				2							3						4
	2x1 3x2																		x4 1,
			x1			x2 2x3																						2,
18)			x1			x2 2x3																						2,
18)			x			x														2x								1,
			x			x					2									2x							4	1,
			1								2																4
	4x					x					2		2x		3					5x						4		2.
			1								2				3											4

			3x2 4x3 5x4 2,										x2 3x3		x4 5,
		x1	x2			x3	x4 1,							x3				0,
19)										20)	x1 x2
		2x	x			2x	x		0,			x		3x	2x			1,
				2				4									4
		1				3						1		3
	3x		3x		2	3x	5x	4	7.		2x			7x	x	4		4.
		1				3						1		3

4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Задача отыскания корней нелинейного уравнения с одним неиз-

вестным вида
f x 0	(4.1)

имеет многовековую историю, но не потеряла своей актуальности и в наши дни. Она часто возникает как элементарный шаг при решении различных научных и технических проблем.

Определение. Совокупность значений переменной x, при которых уравнение (4.1) обращается в истинное тождество, называется решением этого уравнения, а каждое значение x из этой совокупности

корнем уравнения.

Для справедливости большинства рассуждений четвертого раздела достаточно предположить, что в окрестности каждого из искомых корней функции f ( x) дважды непрерывно дифференцируема.


В зависимости от вида функции				f x уравнения вида (4.1) делят
на трансцендентные и алгебраические.
Определение. Функцию f x называют трансцендентной, если
она содержит	показательную		функцию ( y a x ), логарифмическую
функцию	( y loga x),		тригонометрические		функции
(sin x, cos x, tgx,		ctgx), обратные		тригонометрические	функции
(arcsin x, arccos x,		arctg x, arcctg x) и другие.

Предположим, что (4.1) имеет лишь изолированные корни, т.е. для каждого корня такого уравнения существует окрестность, не содержащая других корней этого уравнения.

Задача о нахождении приближенных значений действительных корней (4.1) предусматривает предварительное отделение корня, т. е. установление промежутка, в котором других корней для данного уравнения нет, и уточнение корней с заданной точностью.

На этапе отделения корней область допустимых значений x разбивается на отрезки, на каждом из которых содержится только лишь один корень. Существует два метода отделения корней: графи-

ческий и аналитический.


Так как действительными корнями				уравнения (4.1)	являются
абсциссы точек пересечения			кривой y f ( x) с осью OX ,		то корень
можно отделить графически.			Иногда бывает полезно уравнение (4.1)
записать	в	виде 1( x) 2 ( x). Затем		строят графики	функций
y 1 x	и	y 2 x . Абсциссы точек их пересечения и являются

корнями данного уравнения.

В первом и втором подходах с графиков снимают числа а и b, между которыми расположен корень уравнения (4.1).

Аналитически корни уравнения (4.1) отделяют с помощью известной теоремы математического анализа.

Теорема 4.1. Если непрерывная функция f x принимает значения разных знаков на концах отрезка [а, b], т.е. f a f b 0 , то

внутри этого отрезка существует, по крайней мере, один корень уравнения (4.1).

Далее рассмотрим три метода приближенного вычисления корней нелинейных уравнений.

4.1. Метод простых итераций

Функцию f x представим в виде f x x g x . Соответственно, необходимо решить уравнение вида

x g x .

Поступают следующим образом, корень ищут в виде последовательности приближений xk 1 g xk , где k номер итерации. При

этом l i mxk , g или f 0 , x0 начальное прибли-

жение, которое берут из отрезка [а, b] (в котором находится изолированный корень), можно взять левую границу, т.е. точку а.

Ясно, что подобранное хорошее начальное приближение позво-

лит за малое число итераций найти корень с заданной точностью ε. Условия окончания вычисления элементов последовательности

xk k 0 :

xk 1 xk или f xk .

Пример. Решить уравнение x3 3x 2 0, x (0,1) с точностью

ε = 0,01, т.е. f x* .

Решение. Методом простых итераций найдем корень. Для этого

построим последовательность приближений в виде xk 1					1	2 xk3 .

		x1 0,667 f x1 0, 298;		2
x0 0;
x2 0,568 f x2 0,113;
x3	0,606 f x3 0,041;
x4	0,592 f x4 0,017;
x5	0,598 f x5 0,008 .
Таким образом, x		0,598 x* , потребовалось пять итераций.
	5
Замечание. Для решения нелинейного уравнения				f x 0 со-
вершается переход от функции			f x к функции x x и тогда
организуется итерационный процесс
	xk 1 xk ,		k 0, 1, 2, .

Рассмотрим вопрос поиска функции x . Решение уравнения x x представляет самостоятельный интерес; нахождение его корней называется задачей о неподвижной точке. Это название связано с тем, что точка x* x* при отображении с помощью x из

R в R остается на месте.

Существование и единственность корня уравнения x x

основывается на принципе сжимающих отображений или принципе неподвижной точки.

Определение. Непрерывная функция x называется сжимающей (функцией сжатия) на отрезке [а, b], если:

1. x a,b	x a,b ;
2. q 0,1 :	x2 x1	q	x2 x1	x1, x2 a,b .
2. q 0,1 :	x2 x1	q	x2 x1	x1, x2 a,b .

Теорема 4.2. Пусть функция x определена и дифференцируема на отрезке [а, b]. Тогда, если выполняются условия:

x a,b x a,b		и	q :	x	q 1 x a,b ,

уравнение x x имеет единственный на [а, b] корень x* .
К этому корню сходится определяемая методом простых итера-
ций xk 1	xk последовательность xk k 0,1,2,... , начинающаяся с
любого	x0 a,b . При	этом	справедливы оценки погрешности

k R :

x x

или

x x

1 q

k 1

1 q

Переход от уравнения f (x) 0 к уравнению

x (x) осуществ-

ляется следующим образом: уравнение сначала переписывают в виде x x f (x) , где const , которую необходимо найти. Этот коэф-

фициент можно найти из условия ( x0 ) 0 , где	x0	начальное
приближение.
( x) x f (x) ( x0 ) 1 f ( x0 ) 0		1	.

		f ( x0 )
		f ( x0 )

Или же можно провести иную оценку на основе

(x)

( x)

1 f ( x)

1 1 f

( x)

f ( x)

при условии, что f ( x) 0.

В противном случае вместо уравнения

f (x) 0

рассматривается

уравнение f (x) 0 , если известно, что

0 a f x , x a,b , то	1	.

4.2. Метод половинного деления (метод дихотомии)


Пусть f ( x)		определена и непрерывна на отрезке [а, b] и f (x) 0,
то по теореме 4.1		a,b			f ( ) 0 .

Чтобы определить			ξ выберем произвольную точку c1 (a,b) и
рассмотрим f c1 ( c1 пробная точка):
а) f a f c1 0 a,c1 ,
б) f b f c1 0 c1,b ,
в) f c1 0		c1.
Далее анализируем отрезок, в который попал корень. Например,
если f a	f c1 0 ,		то	на интервале a, c1		выбираем точку
c2 a, c1	и вычисляем значения f c2 , f a и					f c1 . И так про-
должаем до тех пор, пока не выполнится условие							f ci	, где –

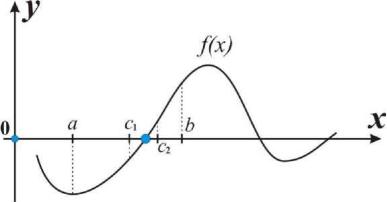
точность вычислений (рис. 4.1).

Рис. 4.1. Графическая иллюстрация метода дихотомии

Если способ задания пробных точек ci определен так, что по-

следовательность длин, получающихся в этом процессе промежутков существования корня стремится к нулю, то методом дихотомии можно найти какой-либо корень уравнения (4.1).

Наиболее распространенным частным случаем метода дихото-

мии является метод половинного деления, реализующий простой способ выбора пробной точки деление промежутка корня пополам,

т.е. c

a b

, c

a c1

или

c1 b

... .

Пример.

Решить уравнение:

x3 3x 2 0,

x 0,1 с точно-

стью ε = 0,01, т.е.

f ( x*)

Решение.

Начнем поиск корня:

f (0) 2,

f (1) 2;

a b

0,5;

f c

0,375;

x* 0; 5,1

0,75;

f c

0,67;

x* 0,5; 0,75

0,625;

f c 0,119;

x* 0,5; 0,625

0,5625;

f c

0,13;

x* 0,5625; 0,625

0,59375;

f c2 0,009;

f c

0,009

0,59375 x*.

4.3.

Метод Ньютона

Одним из популярнейших итерационных методов решения нелинейных уравнений, что связано с его идейной простотой и быстрой

сходимостью, является метод Ньютона.
Будем		считать,		что f x	дважды					дифференцируема	на
a,b ,	a,b ,		f 0.
Необходимо построить последовательность xk , такую,											что
lim xk .
k		xk a,b
Пусть		xk a,b		некоторый	член					последовательности.	По
формуле Тейлора:
	f x f xk f xk x xk							1	f k x xk 2 ,
	f x f xk f xk x xk						2		f k x xk 2 ,
k a,b между точками x и							2
k a,b между точками x и					xk .		Тогда
	f f xk f xk xk					1		f		k xk 2 0.
	f f xk f xk xk							f		k xk 2 0.
					2

Если k известна, то ξ находится из уравнения

				f xk f xk xk	1	f k xk 2	0.
				f xk f xk xk	2	f k xk 2	0.
					2
		Будем считать, что xk близко к			, то расстояние			xk	мало,
		Будем считать, что xk близко к			, то расстояние			xk	мало,
			2
а	x		2	еще меньше, и поэтому этим слагаемым можно пренебречь.
		k

При этом будет найден не корень , а некоторая другая точка xk 1

следующий член последовательности.

Таким образом, итерационный процесс Ньютона определяется

линейным уравнением
f xk f xk xk 1 xk 0				(4.2)
или в явной форме		f xk
x	x	f xk	, k 0, 1, 2,...,
x	x		, k 0, 1, 2,...,
k 1	k	f xk
xk находим до тех пор, пока не выполнится условие					f xk	.
xk находим до тех пор, пока не выполнится условие					f xk	.

Если в равенстве (4.2) фиксированную точку xk 1 заменить переменной x , а 0 в правой части переменной y , то получим уравнение касательной к кривой y f x, проведенной к ней в точке

xk , f xk . Отсюда	геометрический смысл метода Ньютона:
приближения к корню	совершаются по абсциссам точек пересече-

ния касательных к графику данной функции, проводимых в точках, соответствующих предыдущим приближениям (рис. 4.2). Поэтому метод Ньютона называют также методом касательных. Поскольку

процесс итерационный, то необходимо задать начальное приближение
x0 графическим методом. Например, a, b	x0 a.

Рис. 4.2. Графическая иллюстрация метода Ньютона

Пример. Решить уравнение: x3 3x 2 0, x 0,1 с точностью ε = 0,01, т.е. f x* .

Решение. Методом Ньютона найдем корень с заданной точностью. Для этого построим последовательность приближений в виде

xk 1 xk	f xk		,	f x 3x2 3 xk 1		xk	xk3 3xk 2	.

	f xk						3xk3 3
x0 0		f x0 2,0;			x1 0,667	f x1 0, 298;
		x2 0,598			f x2 0,008 .
Следовательно, искомый корень с заданной точностью равен
x* x 0,598.		Потребовались две итерации.
2

4.4. Обобщение методов решения нелинейных уравнений на решение систем нелинейных уравнений

Задача отыскания решений системы нелинейных уравнений более сложная, чем задача отыскания решения одного нелинейного уравнения или системы линейных алгебраический уравнений.

Пусть требуется решить систему уравнений:

f1 x1, x2				,..., xn 0,
		x1, x2		,..., xn			0,
f1		x1, x2		,..., xn			0,
							(4.3)

f	n	x , x	2		,..., x	n	0,
	n	1	2			n

где fi , i 1, n нелинейные функции.

В матричной форме записи система (4.3) принимает вид

F X 0,

где

	f1		x1

F	f2	,	X x2	.


	fn		xn

Рассмотрим два итерационных метода для получения приближенного решения системы (4.3).

Метод простых итераций

Преобразуем систему (4.3) к следующему эквивалентному виду (к виду, удобному для итераций):

x1	1 x1, x2 ,..., xn ,
	2 x1, x2 ,..., xn ,
x1	2 x1, x2 ,..., xn ,	или X X .
..................................		или X X .
..................................

xn n x1, x2 ,..., xn ,

Метод простых итераций определяется рекуррентной формулой:

X (k 1) X (k ) k 0, 1, 2,... .

Вычисления проводятся до тех пор, пока не выполнится условие:

	fi x(k 1)			.
max	fi x(k 1)	или max	xi(k 1) xi(k )	.
i		i
i		i

Итак, задавая начальное приближение

X (0) x1(0) , x2(0) ,..., xn(0) ,

находим последующие приближения по формуле: X (k 1) X (k ) .

Метод Ньютона

Обобщим метод Ньютона для решения одного нелинейного уравнения на решение систем нелинейных уравнений:

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022330.39 Кб2Методическое пособие 64.pdf
#
30.04.20223.05 Mб7Методическое пособие 640.pdf
#
30.04.20223.05 Mб6Методическое пособие 641.pdf
#
30.04.20223.06 Mб2Методическое пособие 642.pdf
#
30.04.20223.07 Mб5Методическое пособие 643.pdf
#
30.04.20223.09 Mб5Методическое пособие 644.pdf
#
30.04.20223.11 Mб3Методическое пособие 645.pdf
#
30.04.20223.11 Mб9Методическое пособие 646.pdf
#
30.04.20223.12 Mб7Методическое пособие 647.pdf
#
30.04.20223.12 Mб23Методическое пособие 648.pdf
#
30.04.20223.17 Mб3Методическое пособие 649.pdf