2. ОПРЕДЕЛИТЕЛИ

2.1.Вычисление определителей

Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, назы-

ваемое определителем или детерминантом n-го порядка этой матрицы. Начнем с определителей второго и третьего порядков.

Пусть дана матрица

тогда ее определитель второго порядка вводится по формуле

Правило вычисления определителя второго порядка: из произведения элементов на главной диагонали вычитается произведение элементов на второй диагонали матрицы А.

В дальнейшем мы не будем приводить матрицу, для которой вычисляется определитель, так как в записи определителя содержатся все элементы соответствующей матрицы.

Определитель третьего порядка вычисляется по форму-

ле

a13 a22 a31 a11 a23 a32 a12 a21 a33.

16

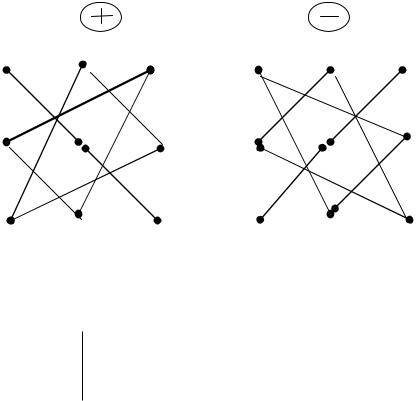
Правило вычисления определителя третьего порядка та-

ково. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком “плюс” берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком “минус” – произведения, сомножители которых стоят не на главной диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).

Порядок определителя равен порядку соответствующей матрицы.

3 1 8 16 90 8 24 20 24 134.

17

2.2.Основные свойства определителя

1.Величина определителя не изменяется, если строки и столбцы этого определителя поменять ролями, т. е.

2.Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число (-1).

3.Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.

4.Умножение всех элементов некоторой строки (столб-

ца) определителя на число равносильно умножению определителя на это число , т. е. общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак определителя:

5.Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.

6.Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

7.Если каждый элемент n-ой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы определителей, первый из которых имеет в n-ой строке (столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель в остальных строках (столбцах), а второй определитель имеет в n-ой строке (столбце) вторые из упомянутых сла-

18

гаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах):

8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель, то величина определителя не изменится.

a21 ... a2n

a21 ... a2n =0. an1 ... ann

Минором элемента aij определителя n-го порядка назы-

вается определитель (n-1)-го порядка, получаемый из данного определителя путем вычеркивания той строки и столбца, на пересечении которых стоит данный элемент. Это число M ij .

Алгебраическим дополнением любого элемента опреде-

лителя называется число, равное минору этого элемента, взятому со знаком (+), если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, есть число четное и со знаком (-) – в противном случае

19

9. Разложение определителя по строке (столбцу).(Один из способов вычисления определителя) Сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца) равна величине этого определителя.

Определитель 3-го порядка разложим по первой строке

Пример 2.2. Вычислить определитель четвертого порядка

Разложить определитель можно по любой строке (столбцу). Однако объем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой больше элементов, равных нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вид

20