Методическое пособие 195

медианой будет значение Me, занимающее серединное значение в ряду. Таким образом, медиана — это значение параметра, которое делит упорядоченный ряд на две равные по объему группы. При нечетном числе измерений, т. е. при n =2i+1, значение параметра для случая i+1 будет медианным. При четном числе измерений (2i) медианой является средняя арифметическая двух значений, расположенных в середине ряда.

Таким образом, формулы для вычисления медианы

напряжения (х1=179, х2=180, х3=181, х4=182, х5=183),т.е.

нечётное число измерений, расположенных в возрастающем порядке. Находим медиану: (2i+1)=5, откуда 2i=4, i=2. По формуле (2.5) получим

Me xi 1 x2 1 x3 181B.

Если из табл. 2.2а взять только четыре значения пробивного напряжения (х1=179,х2=180,х3=181,х4=182), т. e. четное число измерений, то 2i=4, i=2. По формуле (2.6),

Me xi xi 1 x2 x3 180 181 180.5B. 2 2 2

Значение медианы легко определяется графически с помощью кумулятивной кривой (см. рис. 3). Так как по оси ординат отложены накопленные частоты, то, разделив отрезок ординаты, соответствующий 100% наблюдений, пополам и восстановив из его середины перпендикуляр, мы получим медиану геометрически как абсциссу точки пересечения перпендикуляра с кумулятивной кривой.

20

Модой случайной величины называется значение параметра, которое наиболее часто встречается в данном ряду. Условимся обозначать моду через Мо. Для дискретного ряда мода определяется по частотам наблюдаемых значений параметра качества и соответствуют значению параметра с наибольшей частотой.

В случае непрерывного распределения с равными интервалами модальный (т.е. содержащий моду) интервал определяется по наибольшей частоте; в случае неравных интервалов - по наибольшей плотности. Плотность вычисляется как отношение частоты к продолжительности интервала.

Средние величины, характеризуя однородную совокупность одним числом, не учитывают рассеивание наблюдаемых значений параметра качества. Для отображения рассеивания в математической статистике применяют ряд характеристик. Самый простой из них является размах R. Размах представляет собой величину неустойчивую, зависящую от случайных обстоятельств и поэтому применяемую, как правило, в качестве приблизительной оценке рассеивания. Однако, как будет показано ниже, размах бывает очень удобно применять в контрольных картах. Размах R сравнительно легко вычисляется как разность между наибольшим и наименьшем значениями ряда наблюдений:

наблюдаемых значений показывает, как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней. Так как алгебраическая сумма отклонения отдельных значений xi от средней арифметической x равна нулю и непригодна в качестве меры рассеивания, за меру рассеивания принимают сумму квадратов отклонений отдельных значений от средней арифметической, делённую на число наблюдений, уменьшенное на единицу. Эту

21

меру называют выборочной дисперсией и обозначают через s2. Для простой статистической совокупности

i 1

Вместо выборочной дисперсии s2 часто применяют выборочное стандартное отклонение s. Оно имеет ту же

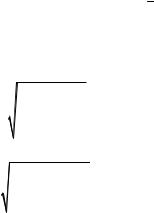
размерность, что и средняя арифметическая x. Выборочное стандартное отклонение для простой статистической совокупности и при наличии частот определяется соответственно по следующим формулам:

арифметической, выраженное в процентах, называют

коэффициентом вариации V:

Коэффициент вариации, который также используется как статистическая характеристика рассеивания, показывает относительное колебание отдельных значений около средней арифметической. Коэффициент вариации, являясь

22

безразмерным, удобен для сравнения рассеивания случайной величины с её средним значением.

3. ВОПРОСЫ К ДОМАШНЕМУ ЗАДАНИЮ

3.1.Что понимается под статистическим рядом и какие его разновидности Вам известны?

3.2.Приведите примеры дискретного и непрерывного изменений случайной величины.

3.3.Как составляется и в дальнейшем заполняется контрольный лист.

3.4.Какие числовые характеристики статистического ряда Вам известны ?

3.5.В чём отличие генеральных и выборочных характеристик?

3.6.Поясните порядок построения наиболее распространенных графиков представления статистического ряда.

3.7.Что такое выборка ?

3.8.Перечислить и охарактеризовать виды выборок.

3.9.Что понимается под абсолютной и относительной частотами ?

3.10.Пояснить способы объединения данных в интервальный ряд.

23

4. ЛАБОРАТОРНОЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕГО ВЫПОЛНЕНИЮ

4.1По выданному преподавателем номеру варианта получить статистические данные измеренного параметра качества.

4.2Построить упорядоченный статистический ряд данных и контрольный листок (по формам А и Б).

4.3Построить интервальный ряд данных.

4.4Построить полигон и гистограмму частот интервального ряда.

4.5Построить кумулятивную кривую частот интервального ряда.

4.6Вычислить среднюю арифметическую величину, медиану, моду и размах статистического ряда данных.

4.7Вычислить выборочную дисперсию, стандартное отклонение и коэффициент вариации.

5.УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА

Вотчете по лабораторной работе №1 указывается следующее: а) наименование лабораторной работы и ее цель; б) результаты выполнения домашнего задания;

в) ход и результаты выполнения лабораторного задания,

где приводятся исходные данные, все расчеты, проводится анализ, делаются выводы, в которых указываются приобретенные при выполнении лабораторной работы знания и навыки.

Студент отчитывается о выполненной и оформленной лабораторной работе на следующем занятии.

6.КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1Как строится упорядоченный статистический ряд ?

6.2Какие данные содержит контрольный листок, как он заполняется и как используется при управлении качеством ?

24

6.3 Как строится и когда используется полигон и гистограмма частот значений измеренного параметра ?

6.4Что такое кумулятивная кривая и как она строится ?

6.5Как вычисляются средняя арифметическая величина, медиана, мода, размах, выборочная дисперсия, стандартное отклонение и коэффициент вариации ? Для каких целей они используются ?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Управление качеством электронных средств: учеб. для ВУЗов по спец. "Проектирование и технология радиоэлектрон. средств" / О.П. Глудкин, А.И. Гуров, А.И. Коробов и др; под ред. О.П. Глудкина. - М.: Высш. шк., 1994. 414 с.

2. Всеобщее управление качеством: учебник для вузов / О.П. Глудкин, Н.М. Горбунов, А.И. Гуров, Ю.В. Зорин; под ред О.П. Глудкина. - М.: Радио и связь, 1999. - 600 с.

3. Статистические методы повышения качества: пер. с англ. / под ред. X. Кумэ. - М.: Финансы и статистика, 1990. 301 с.

СОДЕРЖАНИЕ

СТАТИСТИЧЕСКИЙ РЯД И ЕГО ОБРАБОТКА

ПРИ УПРАВЛЕНИИ КАЧЕСТВОМ В ПРИБОРОСТРОЕНИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе № 1 по дисциплине

«Управление качеством в приборостроении» по направлению подготовки бакалавров 200100.62 «Приборостроение» (профиль «Приборостроение»)

очной и заочной форм обучения

Составители: Данилов Юрий Михайлович Скоробогатов Виктор Сергеевич

В авторской редакции

Компьютерный набор B.C. Скоробогатова

Подписано в печать 28.03.2013. Уч.-изд. л. 1,7. "С"

ФГБОУ ВПО "Воронежский государственный технический университет"

394026 Воронеж, Московский просп., 14

26