5.4. Коллекторная модуляция

Этот вид модуляции осуществляется изменением коллекторного напряжения в такт с модулирующим низкочастотным сигналом и_Ω = cosΩt. Модулирующее напряжение вводится последовательно с напряжением питания Е_{к мол}, определяющим режим молчания:

, (5.16)

где модуляция реализуется в перенапряженном режиме. В максимальной точке режим АЭ критический. Импульс тока, опреде­ляемый входным высокочастотным напряжением u_б = U_б cos ωt и фик­сированным смещением Е_с, имеет постоянный нижний угол отсечки . Остаточное напряжение на коллекторе е_{к min кр} = Е_{к max} - U_к.mах. По мере уменьшения Е_к в импульсе появляется и величивается провал. При Е_к < е_{к min кр} импульс из-за отсечки на уровне S_KpE_K становится трапецеидальным, а верхний угол отсечки Θ! стремится к Θ.

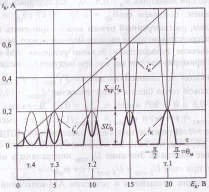
Рис. 20. Временные диаграммы формирования импульсов коллекторного тока при коллекторной модуляции (представленные формы импульсов тока коллек­тора соответствуют точкам 1—4 на рис. 21)

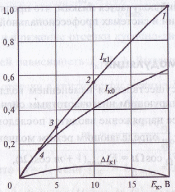
Рис. 21. Статические моду­ляционные характеристики I_к0 (E_к), I_к1,(E_к) (в амперах) и отклонение характеристики I_к1 I_к1 (E_к) от линейной (в амперах)

Процесс формирования импульсов тока i_к(ωt) иллюстрируется на рис. 4.6. Зависимость I_к1 (Е_к) близка к линейной, характеристика I_к0 (E_k) существенно нелинейная (рис. 4.7). В режиме молчания, в котором отклонение от линейной зависимости близко к максимальному, ∆ I_к1/ I_к1mах = 0,068, а для постоянной составляющей ∆ I_к0/ I_{к0 max}= 0,16, т.е. в 2,3 раза больше (численные данные отно­сятся к значению ζ_кр = 0,8).

Расчет модуляционных характеристик. Примем кусочно-линейную модель безынерционного АЭ и рассчитаем сначала зависи­мость I_к1 (Е_к). Расчет выполним двумя способами. Первый, основанный на графическом решении трансцендентных уравнений, предложен СИ. Евтяновым [5].

По условию задачи напряжения Е_с, U₆, cosΘ= -(Е_С- E')/U₆ и сопротивление коллекторной нагрузки R_K считаются постоянными. В результате ток I_к1 в ПР является функцией только напряжения на кол­лекторе:

, (5.16)

где

(5.17)

Формулы (5.16) и (5.17), если считать Е_к параметром, определяют в явной форме семейство I_к1 (U_K) колебательных характеристик уси­лителя. В свою очередь I_к1 и U_K связаны соотношением U_K = I_KR_K, определяющим на плоскости (U_K, I_к1) прямую обратной связи:

I_к1(U _к)=U _к /R _к. (5.18)

Точки пересечения колебательных характеристик с прямой обрат­ной связи, как показано на рис 22, определяют искомую модуляци­онную характеристику I_к1 (Е_К) (см. рис. 21).

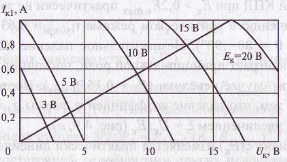
Рис 22. к графическому расчету модуляционных характеристик при коллекторной амплитудной модуляции

На рис. 20, 21 точкам 1 ...4 соответствуют напряжения: 1) E_{K тах} — режим критический; 2) Е_{к мол1} = Е_{к mах}/2 — режим молчания; 3) Е_к = E _KminKp — начало уплощения импульса i_к(ωt) из-за отсечки на уровне S_KpE_{K min кр}; 4) Е_к = 0,6е _min — импульс при U_K = 0 имеет трапецеидальную форму с верхним углом отсечки Θ ₁, близким к Θ.

Графическое решение дает наглядное представление о формиро­вании модуляционной характеристики I_к1 (U_к), но ее расчет оказыва­ется трудоемким. Преобразуем уравнения (5.16)—(5.18) так, чтобы получить параметрическое представление зависимости I_к1 (Е_к). Под­ставим (5.18) в (5.16) и разрешим полученное уравнение относи­тельно U_K:

^, (5.19)

где I_{к1 max} = SU _б γ ₁ (Θ) — амплитуда тока в максимальном режиме.

Параметром в уравнении является верхний угол отсечки Θ₁. Ана­логичное представление E_K(Θ₁) получим из формулы

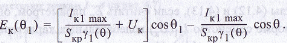(5.20):

Угол отсечки в (5.19), (5.20) меняется в пределах Θ₁ = 0...Θ.

Параметрическое решение удобно для расчетов на ЭВМ (с приме­нением программ типа MathCAD). Таким способом рассчитаны модуляционные характеристики токов (см. рис. 21), электронного КПД и его составляющих, а также зависимости мощностей Р₀, P₁, Р_рас от напряжения Е_к (рис. 23).

Обратим внимание на особенности зависимостей η_{э кр} Электронный КПД при Е_к > 0,2Е_{К тах} практически не зависит от Е_к и близок к значению в критическом режиме ц_{э кр} = 0,63...0,72 (ζ_кр = 0,8...0,85, Θ = 80...90°). Незначительное падение КПД при Е_к < 0,2Е_{к mах} не играет принципиальной роли, поскольку мощности Р₀ и P₁, в данном случае невелики (Р₁ = 0,15P _{1 мол}). Постоянство КПД объясняется тем, что падение коэффициента формы g₁ = I_к1 / I_к0 ком­пенсируется увеличением ζ, = U_K/E_K (рис. 4.9, а).

Коэффициент ζ,(Е_К) изменяется практически линейно от значения ζ_кр в максимальном режиме до ζ₀ ^ПР^И Е_к → 0:

ζ=ζ ₀ -(ζ ₀ -ζ _кр) Е_к /Е _{к max} (5.21)

При линейной аппроксимации (5.21) зависимость I_к1 (Е_K) = ζE_K/R_K описывается параболой, а коэффициент гармоник определяется вто­рой гармоникой частоты модуляции:

К_Г = 0,5hm², (5.22)

где h = 0,25(ζ₀/ζ_кр - 1). Согласно расчетам по формулам (4.15), (4.16) в области ζ_кр = 0,7...0,82; Θ = 75...90° имеем h ≈ 0,07, и, следова­тельно, коэффициент гармоник изменяется от 1,7 % при m = 0,7 до 3,5% при m = 1. При дальнейшем увеличении ζ_кр значение К_Г несколько уменьшается, но при ζ_кр < 0,9 остается достаточно высо­ким: К_Г ≈ 2,5 % при m = 1.

Модуляционные характеристики на рис. 23, б рассчитаны по фор­мулам:

Р₀ = E_кI_к0 ; Р₁ = I²_к1 /R _к ; P_рас = Р₀ - Р₁ (5.23)

При линейных зависимостях 1_к0(Е_к), 1_к1(Е_к) зависимости мощностей от Е_к имеют вид парабол, например Р₁ = Р_{1 max}(E_K/E_{K max}) ² . Рас­четная зависимость Р₁ (Е_К) в (5.23) удовлетворительно аппроксимируется параболой степени 3/2: Р₁ = Р_{1 max} (E_K/E_{K max}) ^3/2.Из-за недостаточной линейности и других недостатков, отмечен­ных далее, простая коллекторная модуляция в технике передающих устройств, как правило, не применяется.