3. Лабораторные задания и методические указания по их выполнению

Измерить в полосе частот 8,5-12,0 ГГц с шагом 0,25 ГГц следующие характеристики волноводного направленного ответвителя на основе двух прямоугольных волноводов 23х10 мм2 с общей узкой стенкой и тремя отверстиями связи:

1) частотную характеристику КСВ по входу;

2) частотную характеристику рабочего затухания;

3) частотную характеристику переходного ослабления;

4) коэффициент развязки между выходными основным и боковым плечами.

При проведении измерений к неиспользуемым плечам ответвителя необходимо подключать согласованные нагрузки.

Полученные результаты оформить в виде таблицы.

4. Содержание отчета

В отчете должны быть представлены:  краткая теория направленных ответвителей, описание их электрических характеристик, результаты измерений характеристик исследованного направленного ответвителя и выводы.

5. Контрольные вопросы

1. Волноводные Е- и Н-тройники, их свойства, применение в СВЧ-технике.

2. Двойной волноводный Т-мост, его свойства, применение в СВЧ-технике.

3. Балансный делитель (сумматор) мощности и его свойства.

4. Направленные ответвители и мосты, их основные электрические параметры и применение в СВЧ-технике.

5. Методика исследования характеристик направленных ответвителей.

Лабораторная работа № 5 исследование пассивных невзаимных устройств свч

Цель работы

1. Изучение конструкций и основных свойств невзаимных и взаимных устройств СВЧ на основе волноводов с намагниченными ферритами.

2. Экспериментальное исследование характеристик резонансного ферритового вентиля но основе прямоугольного металлического волновода.

Домашнее задание: изучить теоретический раздел работы.

1. Свойства свч ферритов. Гиромагнитные эффекты в намагниченных ферритах

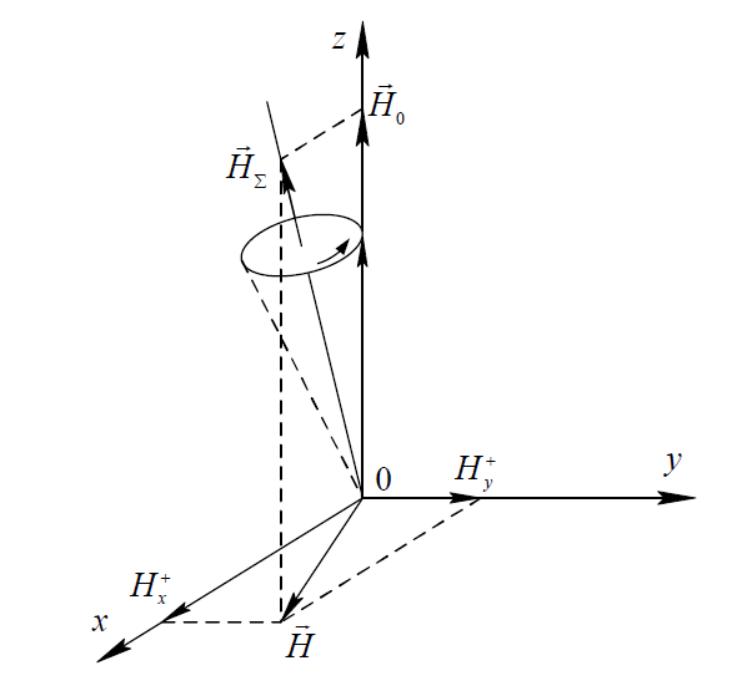
Использование ферритов на СВЧ обусловлено рядом специфических эффектов, возникающих при распространении электромагнитных волн в намагниченной ферритовой среде. Ферритовые приборы применяются в СВЧ и КВЧ диапазонах в качестве развязывающих устройств (вентилей и циркуляторов), поляризаторов, перестраиваемых резонаторов и фильтров. Основные характеристики и параметры этих устройств определяются свойствами ферритов, представляющих собой смеси оксидов железа и других металлов (марганца, кобальта, никеля, цинка, кадмия, магния). Ферриты – это трудно механически обрабатываемые керамические материалы с высоким удельным сопротивлением (более 10⁶ Ом∙см) с относительной диэлектрической проницаемостью ε_r=5–20 и низким тангенсом угла диэлектрических потерь tgδ_э=10^-3–10^-4. Начальная относительная магнитная проницаемость СВЧ ферритов в слабых низкочастотных полях μ=10–3000. На СВЧ при отсутствии постоянного намагничивающего поля μ ферритов лишь незначительно отличается от единицы. Структура ферритов может быть моно- и поликристаллической. Монокристаллы – это правильные многогранники с упорядоченной кристаллической решеткой во всем объеме; поликристаллы состоят из большого числа хаотически сросшихся мелких кристаллов. Ферритовые образцы состоят из доменов – мелких областей, намагниченных до насыщения. Размеры домена очень малы – менее 1 мкм. Поскольку векторы намагниченности доменов в отсутствие внешнего магнитного поля имеют произвольную пространственную ориентацию, образец в целом может быть ненамагниченным. С ростом температуры вследствие нарушения ориентации магнитных моментов электронов намагниченность доменов уменьшается и при температуре Кюри порядка t_c=100-600 °С она исчезает. Магнитные свойства ферритов определяются наличием в их кристаллической решетке «магнитных частиц» – атомов или ионов, обладающих векторным магнитным моментом m. Такой момент обусловлен нескомпенсированными спиновыми магнитными моментами m_сп электронов атома (орбитальные моменты дают незначительный вклад в суммарный магнитный момент атома). Рассмотрим «магнитный» атом, находящийся в постоянном магнитном поле напряженностью Н₀ (рис. 1). Пусть магнитный момент атома m составляет с вектором Н₀ некоторый угол α. Под действием возникшего со стороны магнитного поля момента силы механический момент атома L и магнитный момент m начинают прецессировать (вращаться) вокруг направления Н₀. Таким образом, вектор m описывает в пространстве конус с осью в виде вектора Н₀. Соответственно, так же прецессирует и суммарный вектор намагниченности феррита М. Если смотреть по направлению постоянного магнитного поля Н₀ (вдоль оси OZ), вращение векторов m и М происходит по часовой стрелке. Частота прецессии

, (1)

где – гиромагнитная постоянная (e – заряд, m_e - масса электрона), называется круговой частотой ферромагнитного резонанса. Вследствие взаимодействия «магнитных» атомов друг с другом и с кристаллической решеткой угол прецессии α постепенно уменьшается, и за время порядка 10^-7-10^-9 с (время релаксации) становится равным 0. Магнитные моменты всех атомов выстраиваются по направлению Н₀, так же ориентируется и вектор намагниченности М (величина М есть предел отношения результирующего магнитного момента феррита к его объему при стремлении последнего к нулю) и феррит оказывается намагниченным.

Пусть в феррите вместе с постоянным действует переменное магнитное поле с частотой ω, описываемое вектором Н, поляризованным в плоскости XOY, причем амплитуда Н<<Н₀. Поскольку на магнитные моменты атомов теперь действует суммарное поле Н_Σ (рис. 1), вектор намагниченности феррита теперь имеет постоянную и переменную составляющие: М=М₀+М_ω и вращается вокруг направления Н_Σ. Если переменного магнитного поля нет, направление вектора М=М₀ совпадает с направлением вектора Н₀.

Возникновение преимущественной угловой ориентации магнитных моментов атомов и вектора намагниченности феррита М приводит к тому, что электромагнитная волна воспринимает намагниченный феррит как анизотропную среду, в которой вектор магнитной индукции B=||μ||H, где ||μ|| - тензор абсолютной магнитной проницаемости.

Из электродинамики известно, что для феррита, намагниченного полем Н₀ вдоль оси OZ, тензор магнитной проницаемости имеет вид

, (2)

где ; ; – параметр, имеющий размерность частоты, определяемый свойствами феррита; μ₀ = 4π10^-7 Г/м – абсолютная магнитная проницаемость свободного пространства.

Тензор ||μ|| является антисимметричным. Это свидетельствует о наличии гиротропных свойств у намагниченного феррита, выражающихся в специфических явлениях, сопровождающих распространение ЭМВ в такой среде (в частности, вращение плоскости поляризации ЭМВ).

а) б)

Рис. 1. К пояснению свойств намагниченного феррита

В развернутом виде выражение (2) имеет вид:

,

где μ, k – комплексные элементы тензора магнитной проницаемости, зависящие от Н₀ и частоты ω.

Таким образом, если вектор Н высокочастотного поля параллелен оси OZ, т.е. H_x=H_y=0, H_z=H, то вектор магнитной индукции имеет единственную компоненту B_z=μ₀H, и гиромагнитные свойства в феррите не проявляются. Если же вектор магнитного поля Н имеет круговую поляризацию и плоскость вращения перпендикулярна намагничивающему полю, то вектор магнитной индукции также имеет круговую поляризацию, по направлению совпадающую с вектором Н. Действительно, положим H=x₀H±jy₀H, где x₀, y₀ – единичные векторы прямоугольной системы координат; нижний знак соответствует круговой поляризации правого вращения (по часовой стрелке, если смотреть в направлении Н₀), а верхний – левого вращения (против часовой стрелки, если смотреть в направлении Н₀). Найдем B_x , B_y и B_z:

– для правого вращения; (3)

– для левого вращения. (4)

В этих выражениях μ₊ и μ_– – комплексные абсолютные магнитные проницаемости феррита для волн круговой поляризации правого и левого вращений соответственно. Различные значения μ₊ и μ_– приводят к различию постоянных распространения и (ε=ε₀ε_r – абсолютная диэлектрическая проницаемость феррита) и, естественно, фазовых скоростей волн с круговой поляризацией вектора Н правого и левого вращения. Зная направление и величину намагничивающего постоянного поля Н₀, вычислив действительную и мнимую части μ₊ и μ_–, представив высокочастотное поле Н в виде линейной комбинации полей с круговой поляризацией правого и левого вращений, можно охарактеризовать происходящие в феррите гиромагнитные эффекты.

На рис. 2 представлены зависимости действительных и мнимых частей относительных магнитных проницаемостей и от величины намагничивающего поля Н₀ . Мнимые части _{характеризуют потери энергии электромагнитного поля СВЧ. Резонансные свойства феррита характеризуются шириной линии ферромагнитного резонанса 2ΔН, определяемой по уровню Поэтому}

_{2ΔН=1/(πγτ0),}

_{а добротность феррита определяется относительной шириной линии ферромагнитного резонанса}

_{Q=Н0/(2ΔН).}

В ферритовых образцах конечных размеров внутреннее магнитное поле отличается от внешнего, в котором находится образец. Поэтому частота ферромагнитного резонанса зависит от формы образца и его ориентации относительно внешнего магнитного поля.

а) б)

Рис. 2. Зависимости действительных и мнимых частей относительных магнитных проницаемостей феррита от величины намагничивающего поля

На рис. 2 отмечены четыре области намагничивания, используемые в ферритовых устройствах СВЧ.

В области I (при Н₀<<Н_рез.) значения _{, а положительны и различны. Поэтому различаются} постоянные распространения и и _{фазовые скорости} и _{распространения ЭМВ с правым и левым направлениями вращения плоскости поляризации вектора Н. Это явление используется в приборах, работающих на основе различия фазового сдвига волн левого и правого вращения при прохождении ими слоя феррита, например, в поляризаторах на эффекте Фарадея, циркуляторах и фазовращателях СВЧ.}

В области II (при Н₀<Н_рез.) значения _{, а При этом феррит существенно искажает структуру поля волны с правым вращением вектора Н. Это явление при Н0=Нсм используется в вентилях со смещением поля, а при Н0=Н┴ (когда )} – _{в вентилях на основе поперечного ферромагнитного резонанса.}

В области III (при Н₀~Н_рез.) _{, что приводит к резкому возрастанию поглощения ферритом энергии волны с правым вращением вектора Н из-за ферромагнитного резонанса. При совпадении частоты СВЧ колебаний ω с частотой ферромагнитного резонанса ωН волна с правым вращением вектора Н создает силу, вызывающую вынужденную незатухающую прецессию магнитных моментов атомов и вектора намагниченности феррита, следовательно, энергия волны СВЧ колебаний будет интенсивно поглощаться ферритом. Это явление используется в резонансных ферритовых вентилях.}

Область IV (при Н₀>Н_рез.) используется для реализации зарезонансных циркуляторов.

Продольное распространение электромагнитных волн в намагниченном феррите

Пусть в намагниченном до насыщения феррите вдоль направления намагничивания (ось OZ) распространяется плоская линейно-поляризованная ЭМВ. Из уравнений Максвелла следует, что поле этой волны поперечно, т.е. продольные компоненты векторов Е и Н равны нулю. При этом проявляется эффект Фарадея, заключающийся в повороте плоскости поляризации волны на некоторый угол φ при прохождении через продольно намагниченный феррит (см. рис. 3). Значение намагничивающего поля Н₀ должно соответствовать области 1 на рис. 2. Линейно поляризованная волна может быть представлена в виде комбинации равноамплитудных волн с круговыми поляризациями векторов Н и Е правого и левого вращений с различными постоянными распространения и характеристическими сопротивлениями:

и , и .

Подчеркнем, что для волн с круговой поляризацией намагниченный феррит будет представлять собой изотропную среду с абсолютной диэлектрической проницаемостью ε и скалярными абсолютными магнитными проницаемостями μ₊ ≠μ_- .

Фазовые скорости этих волн также будут различными:

и .

Из-за различия магнитных проницаемостей феррита для этих волн они имеют различные фазовые скорости и приобретают различные фазовые набеги при распространении на одинаковое расстояние. Таким образом, линейно-поляризованная волна распространяется в феррите с фазовой скоростью

,

где – среднее значение постоянных распространения волн с поляризациями правого и левого вращения. На выходе ферритовой среды в результате сложения волн с круговыми поляризациями вновь возникает линейно-поляризованная волна; текущий угол φ(z), образуемый ее плоскостью поляризации с осью OX, определяется выражением

При прохождении волной в феррите расстояния L плоскость поляризации повернется на угол (рис. 3, а)

Поворот плоскости поляризации всегда происходит по часовой стрелке, если смотреть в направлении вектора намагничивающего поля Н₀ и не зависит от направления распространения волны, т.е. эффект Фарадея является невзаимным эффектом: при распространении волны в обратном направлении вектор Н дополнительно повернется на угол φ и окажется повернутым относительно исходного положения на угол 2φ(L) (рис. 3, б).

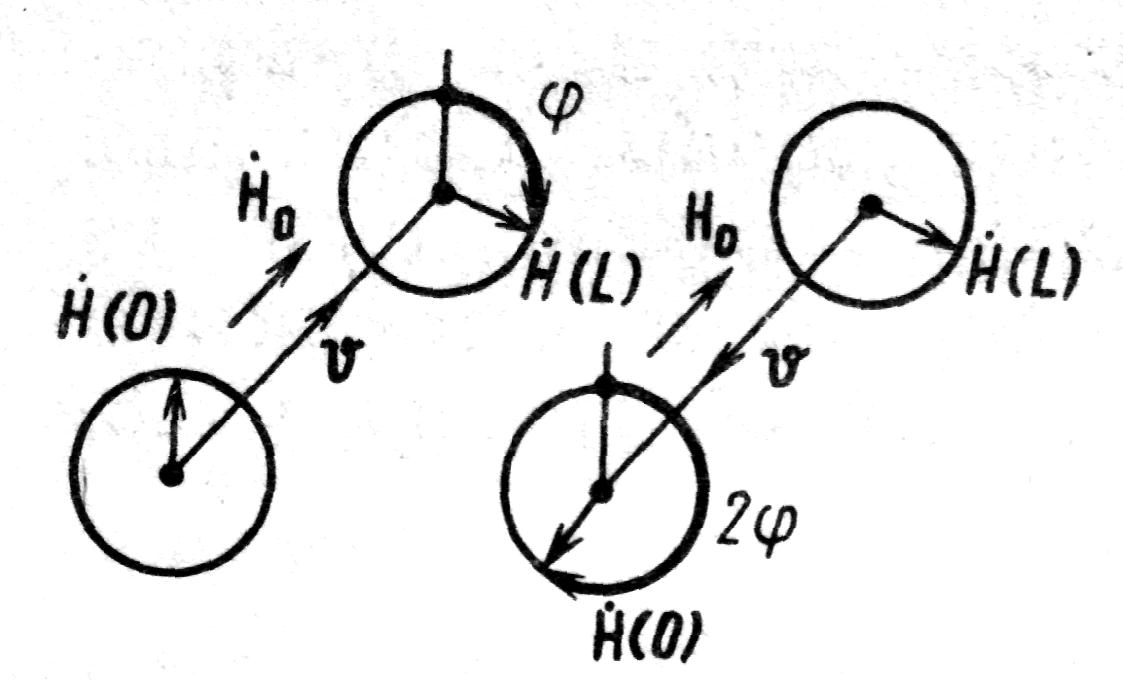
Рис. 3. Невзаимное вращение плоскости поляризации ЭМВ в продольно-намагниченном феррите (эффект Фарадея)

Электрическое поле рассматриваемой волны при этом имеет эллиптическую поляризацию, поскольку характеристические сопротивления волн с поляризацией правого и левого вращения различны и, соответственно, Е_x ≠E_y.

Эффект Фарадея проявляется и в продольно-намагниченной плазме, которая характеризуется тензором ||ε||.

С учетом выражений для μ и k, входящих в тензор магнитной проницаемости, абсолютные магнитные проницаемости μ₊ и μ_- для волн с круговой поляризацией правого и левого вращения могут быть представлены в виде

; .

Очевидно, что при совпадении частоты волны с частотой прецессии магнитных моментов атомов ω=ω_H скалярная магнитная проницаемость для волны с круговой поляризацией правого вращения μ₊ стремится к бесконечности, и, следовательно, фазовая скорость этой волны – к нулю (без учета потерь) и распространение волны прекращается. Частота ω_H=ω_H1 называется круговой частотой продольного ферромагнитного резонанса.

С другой стороны, при ω=ω_H энергия волны с круговой поляризацией правого вращения будет затрачиваться на поддержание вынужденной прецессии магнитных моментов атомов и эта волна будет интенсивно затухать, о чем говорит резонансное возрастание при Н₀=Н_рез (рис. 2, б). Это явление называется продольным ферромагнитным резонансом и наблюдается только для волны с правой круговой поляризацией, волна же с круговой поляризацией левого вращения будет распространяться в феррите практически без ослабления.

Поперечное распространение электромагнитных волн в намагниченном феррите

Пусть в намагниченном до насыщения феррите перпендикулярно направлению намагничивания (ось OZ), например, вдоль оси OX распространяется плоская линейно-поляризованная волна (рис. 1).

При нормальном падении на поперечно-намагниченную ферритовую пластину волны с вектором Н, вращающимся в поперечной плоскости, и совпадении положений вектора Е волны и вектора Н_0, в случае круговой поляризации левого вращения волна будет проходить сквозь пластину практически без ослабления; случае круговой поляризации правого вращения при ω=ω_H возникнет ферромагнитный резонанс и волна будет интенсивно затухать как и при продольном ферромагнитном резонансе.

При нормальном падении линейно-поляризованной волны на поперечно-намагниченную пластину и несовпадении положений вектора Е волны и вектора Н₀ , в пластине, как следует из уравнений Максвелла, одновременно возбуждаются обыкновенная и необыкновенная волны, которые вследствие разности фазовых скоростей в пластине на ее выходе оказываются несинфазными и, суммируясь, дают волну эллиптической поляризации. Явление преобразования гиротропной пластиной линейно поляризованной волны в волну с эллиптической поляризацией называется эффектом Коттона-Мутона (эффект магнитного двойного лучепреломления). При выключении постоянного намагничивающего поля необыкновенная волна исчезает и двойное лучепреломление не возникает.

У обыкновенной волны электромагнитное поле поперечное, ее постоянная распространения и характеристическое сопротивление определяются выражениями

, .

Обыкновенная волна распространяется в феррите и при отсутствии поля Н₀ как в изотропном диэлектрике с абсолютными магнитной μ₀ и диэлектрической ε=ε₀ε_r проницаемостями и представляет собой поперечную (Т) волну.

У необыкновенной волны электрическое поле линейно поляризовано (в данном случае в плоскости YOZ), а магнитное поле имеет эллиптическую поляризацию в плоскости распространения XOZ, поскольку вектор Н имеет как поперечную, так и продольную составляющие, что характерно для волны Н-типа. Постоянная распространения, фазовая скорость и характеристическое сопротивление необыкновенной волны определяются выражениями

, .

Обозначим . Очевидно, что при μ=0 фазовая скорость необыкновенной волны стремится к нулю, т.е. в отсутствие потерь эта волна не может распространяться в феррите. Это явление имеет место на частоте

,

называемой круговой частотой поперечного ферромагнитного резонанса. При наличии диэлектрических потерь волна распространяется, но интенсивно затухает, поскольку волновое число β₂ становится комплексным, а при некотором значении намагничивающего поля , μ₂ стремится к бесконечности, следовательно, мнимая часть волнового числа β₂, определяющая потери энергии СВЧ поля в феррите, тоже стремится к бесконечности.

Таким образом, затухание волны при поперечном ферромагнитном резонансе вызвано наличием диэлектрических потерь в феррите. Надо отметить, что напряженность намагничивающего поля , при которой наступает поперечный ферромагнитный резонанс, оказывается значительно меньшей Н_рез. (рис. 2). Это облегчает построение вентилей, позволяя использовать постоянные магниты с меньшей массой и габаритами. Поперечный ферромагнитный резонанс является невзаимным эффектом.

Эффект смещения поля

Эффект смещения поля возможен и в продольных, и в поперечных магнитных полях в случае μ<k. При этом величина намагничивающего поля Н_см должна соответствовать области II на рис. 2, а. В этой области значение действительной части магнитной проницаемости феррита для волн правого вращения оказывается , что соответствует мнимому значению постоянной распространения . Поэтому такая волна в ферритовом образце конечных размеров будет иметь экспоненциально убывающую амплитуду, как в запредельном волноводе. Распространение волны в нем невозможно и поле вытесняется из образца. Так как образец, как правило, размещается в линии передачи (например, в волноводе), это вытеснение приводит к смещению и искажению всей структуры поля волны с круговой поляризацией правого вращения. При этом волна с круговой поляризацией левого вращения, для которой _, распространяется в феррите как в обычном диэлектрике с повышенными значениями диэлектрической и магнитной проницаемостей. Эффект смещения поля является невзаимным.