12. Цифровая обработка сигналов

1. Структура и характеристики цифрового фильтра

Цифровым фильтром называется вычислительное устройство, реализующее алгоритм работы согласно следующему уравнению в конечных разностях:

₍₁₂₂₎

где x_p(kT) отсчеты входного сигнала; y_p(kT) - отсчеты выходного сигнала; a_mb_i,- коэффициенты.

Линейные цифровые фильтры делятся:

- на устройства с постоянными параметрами, у которых все коэффициенты a_mb_i, есть константы, и с переменными параметрами, не отвечающие данному требованию;

- на фильтры нерекурсивные (другое название - транверсальные), у которых все коэффициенты b_i=0, вследствие чего выходной сигнал зависит только от входного, и рекурсивные при b_i≠0, что означает наличие обратной связи.

Рассмотрим сначала структуру и характеристики нерекурсивного цифрового фильтра с постоянными параметрами. Для такого фильтра получим уравнение в конечных разностях:

₍₁₂₃₎

Применив Z-преобразование получим для передаточной функции нерекурсивного фильтра:

₍₁₂₄₎

Путем подстановки. z=θ^jɷT найдем выражение для комплексной частотной характеристики нерекурсивного фильтра:

₍₁₂₅₎

Для амплитудно-частотной характеристики нерекурсивного фильтра получим:

₍₁₂₆₎

Для фазочастотной характеристики имеем:

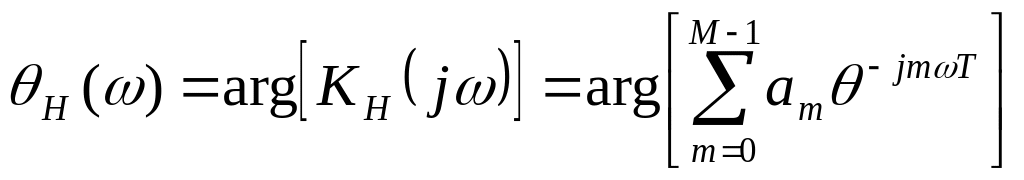(127)

₍₁₂₈₎

Прямая форма реализации временной характеристики приводит к структуре нерекурсивного цифрового фильтра, представленной на рис. 60.

На схеме рис. 60 звено означает задержку входного импульса на время , равное времени дискретизации входного аналогового сигнала. Z-образ такого звена есть .

Импульсная характеристика цифрового фильтра есть его реакция на единичный дельта-импульс имеет вид:

₍₁₂₉₎

где (k-m)T - единичный дельта-импульс.

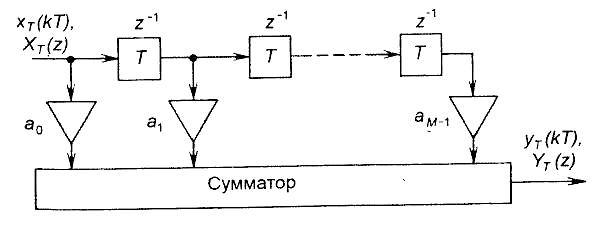
Рис. 60

Частотная характеристика нерекурсивного фильтра, как и спектр дискретного сигнала, является периодической функцией с частотой повторения F=1/T. Максимум АЧХ соответствует значению частоты f_m=mF₁, где m - целое число. Форма АЧХ и ФЧХ зависит от комбинации коэффициентов a_m, собранных в вектор а.

2. Цифровой фильтр

Применив Z-преобразование, получим для передаточной функции рекурсивного фильтра:

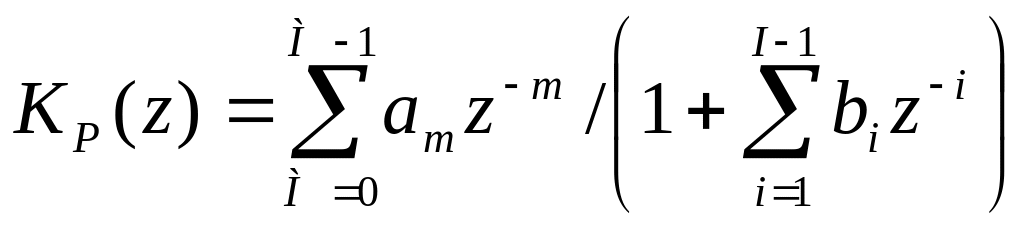₍₁₃₀₎

Путем подстановки z=e^jɷT найдем выражение для комплексной частотной характеристики рекурсивного фильтра:

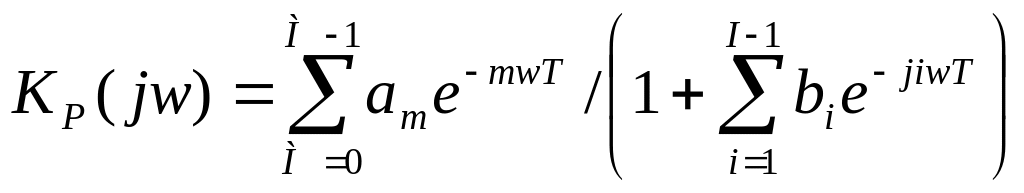₍₁₃₁₎

Для амплитудно-частотной характеристики рекурсивного фильтра получим:

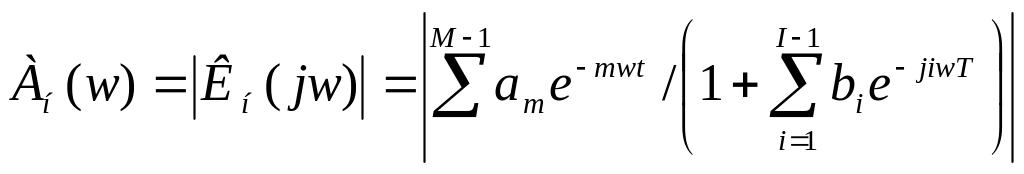
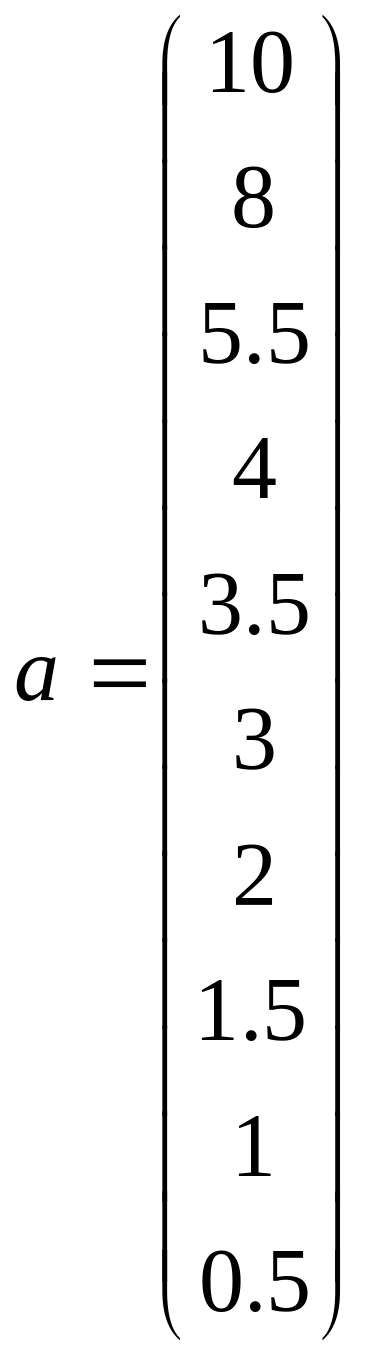
T=0.5 m=10 m1=1

m=0...M1

Для фазочастотной характеристики имеем

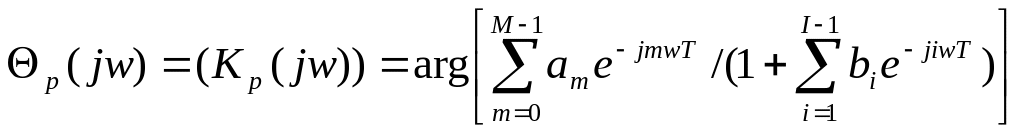₍₁₃₂₎

На рис. 61 приведена программа по расчету амплитудно-частотной и фазочастотной характеристик (АЧХ и ФЧХ) рекурсивного цифрового фильтра при заданных значениях коэффициентов a₀, a₁, a_2,…a_M-1 собранных в вектор а, коэффициентов b₀, b₁, b₂…b_j-1, собранных в вектор b, и шаге дискретизации T. В программе приняты те же обозначения, что и в перечисленных формулах.

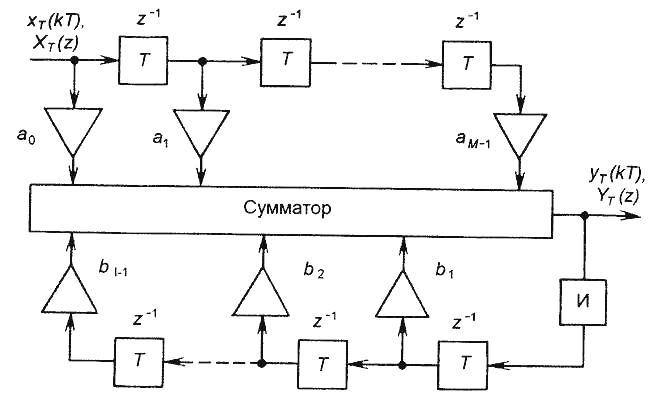
Рис. 61

Частотная характеристика рекурсивного фильтра, как и спектр дискретного сигнала, является периодической функцией с частотой повторения F=1/T. Форма АЧХ и ФЧХ зависит от комбинации коэффициентов a_m и b_H собранных соответственно в векторы a и b. Пример расчета при М = 10, l = 10 трех характеристик цифрового фильтра по программе приведенной ниже показан на рис. 62, на котором АЧХ построена в двух масштабах.

Следует отметить существенные различия в характеристиках нерекурсивного и рекурсивного цифровых фильтров, причиной чему является наличие в последнем обратной связи. Эти различия приводят в рекурсивном фильтре к возможности получения более узкой АЧХ, к сложному, колебательному виду ФЧХ и возможной потере устойчивости.

Под устойчивостью цифрового фильтра понимается ограниченность амплитуды выходного сигнала при любых начальных условиях и ограниченном входном сигнале x_T(kT). Одним из критериев такой устойчивости является расположение полюсов z_j, передаточной функции, т.е. корней знаменателя функции K_P(z), внутри единичной окружности на z-плоскости.

В этом отношении устойчивость цифрового рекурсивного фильтра во многом напоминает линейную цепь непрерывного типа с обратной связью, устойчивость которой также определяется по расположению нулей и полюсов на плоскости комплексной переменной.

Одним из признаков устойчивости цифрового фильтра является отсутствие неограниченного возрастания пикового значения АЧХ.

Другой важной проблемой при анализе работы цифрового фильтра является возникновение в нем помехи, называемой шумом квантования, связанной с преобразованием на входе фильтра аналогового сигнала в цифровой. Рассмотрим подробнее данный вопрос. Квантование сигнала есть представление его отсчетов с помощью конечного числа n разрядов.

При двоичном коде квантование приводит к получению N=2” возможных комбинаций или уровней квантования, на которые может быть разбит по амплитуде входной аналоговый сигнал. Амплитуда сигнала и его мощность на нагрузке 1 Ом при этом составят (рис. 63):

, ₍₁₃₃₎

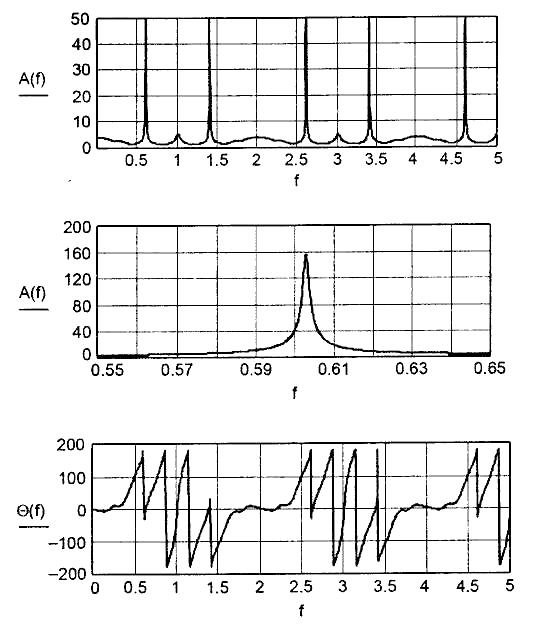
Рис. 62

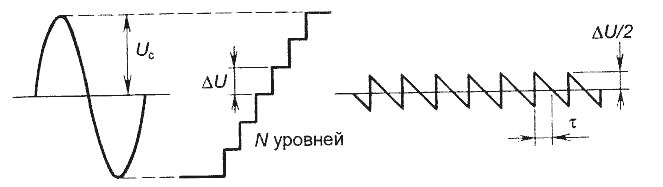
Рис. 63

В первом приближении ошибка квантования не превышает половины одного уровня квантования, составляя U_n=ΔU/2, а по виду близка к треугольной форме u_n(t)=U_nt/τ. Эту ошибку можно трактовать как шум квантования или помеху, мощность которой на нагрузке 1 Ом составит:

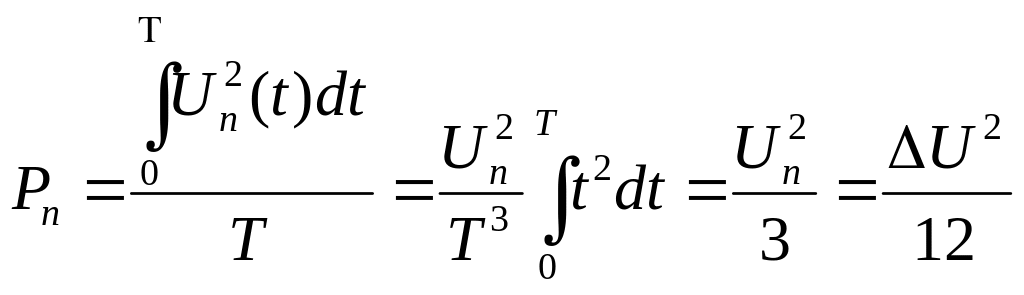₍₁₃₄₎

На основании двух последних выражений и равенства N=2ⁿ для отношения мощностей сигнал/помеха за счет шумов квантования получим:

₍₁₃₅₎

или (дБ)

Отношение сигнал/помеха за счет шумов квантования составляет ориентировочно 6 дБ на один разряд квантования.

Функцию цифрового фильтра может выполнять сигнальный микропроцессор, программируемый согласно уравнениям в конечных разностях. Одновременно он может выполнять функции аналого-цифрового (АЦП) и цифро-аналогового преобразователей (ЦАП).