
- •Введение
- •Электромагнитные волны
- •Основные законы электромагнитного поля
- •Электромагнитные волны и их свойства
- •Общие вопросы распространения радиоволн. Основные определения
- •Тропосфера
- •Строение и основные параметры тропосферы
- •Влияние тропосферы на распространение земных радиоволн. Явление тропосферной рефракции
- •Состав и строение верхних слоев атмосферы
- •Особенности распространения сверхдлинных и длинных радиоволн
- •Общие сведения
- •Скорость распространения
- •Особенности распространения средних волн
- •Антенны. Общие понятия
- •Назначение и классификация антенн
- •Назначение передающей и приемной антенн
- •Структурная схема антенны
- •Расчет электромагнитных полей излучающих систем в дальней, промежуточной и ближней областях
- •Векторная комплексная диаграмма направленности антенны
- •Рабочая полоса частот и предельная мощность антенны
- •Шумовая температура приемной антенны
- •Взаимное сопротивление разнесенных антенн
- •Передающая антенна как четырехполюсник
- •О передаче мощности между двумя антеннами
- •Антенна как открытый колебательный контур
- •Общие характеристики антенн
- •Сопротивление излучения
- •Сопротивление потерь
- •Полное активное сопротивление антенны
- •К. П. Д. Антенны
- •Входное сопротивление антенны
- •Характеристики направленности антенны
- •Диапазонные свойства антенны
- •Максимальное напряжение в антенне
- •Эксплуатационные характеристики передающей антенны
- •Формулы идеальной радиопередачи
- •Мощность, отдаваемая приемной антенной приемнику
- •Антенны длинных и средних волн
- •Виды антенн
- •Ромбические антенны
- •Антенна бегущей волны
- •Информация в радиотехнических системах
- •Классификация радиотехнических систем
- •Количество и характер информации
- •Вероятностное описание сообщений (непрерывных, импульсных, цифровых)
- •Классификация ртс по характеру сообщений
- •Основы телевидения
- •Телевизионные радиопередатчики. Общая характеристика
- •Телевизионные приемники
- •Системы телевидения. Основные понятия и принципы
- •Телевизионная развертка изображений
- •Кодирование сигналов в системах цветного телевидения
- •Телевизионный приемник цветного изображения
- •Сотовые системы связи
- •Радиальные системы с каналами общего доступа. Сотовые системы I поколения (аналоговые)
- •Системы с сотовой структурой
- •Космические радиолинии
- •Радиолинии «земля — космос», «космос — земля», «космос — космос»
- •Ретрансляционные радиолинии
- •Принцип радиорелейной связи
- •Классификация радиорелейных линий
- •Цифровая обработка сигналов
- •Структура и характеристики цифрового фильтра
- •Цифровой фильтр
- •Синтез цифрового фильтра
- •Устройства питания
- •Назначение и параметры
- •Выпрямители
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Расчет электромагнитных полей излучающих систем в дальней, промежуточной и ближней областях
При теоретических исследованиях излучающие системы антенн обычно предполагаются расположенными в неограниченном однородном пространстве. Это существенно облегчает задачу расчета электромагнитных полей и сохраняет возможность впоследствии учесть влияние Земли и окружающих предметов с помощью методов теории дифракции.
Как известно из
основ электродинамики, векторные
потенциалы электромагнитного поля,
создаваемого известным распределением
возбуждающих электрических и магнитных
токов
![]() в произвольной точке наблюдения
в произвольной точке наблюдения
![]() ,
определяются выражением:
,
определяются выражением:
![]() (17)
(17)
где
![]() — расстояние между точками наблюдения
Р и интегрирования Q;
— расстояние между точками наблюдения
Р и интегрирования Q;
![]() ;
V — объем, занимаемый токами излучающей
системы.
;
V — объем, занимаемый токами излучающей
системы.
Выражение (17) представляет строгое решение векторных неоднородных уравнений Гельмгольца. Это решение является единственным, поскольку удовлетворяет условию излучения на бесконечности и имеет всюду конечное значение. Далее можно определить векторы полей Е и Н для любой точки пространства. Сокращенно можно записать:
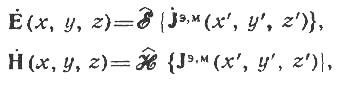
где
![]() и
и
![]() — векторные интегродифференциальные
операторы, задающие последовательность
вычислений нужных компонентов поля.
Операторы
— векторные интегродифференциальные
операторы, задающие последовательность
вычислений нужных компонентов поля.
Операторы
![]() и
и
![]() ставят в соответствие заданному
распределению электрических или
магнитных токов в области V
распределение полей E
и Н в пространстве. Эти операторы
являются строгими и применимы при
любых взаимных расположениях точек
источников и точек наблюдения. Однако,
идя по такому пути, как правило, не
удается получить простых замкнутых
выражений даже для сравнительно
простых излучающих систем. Потому
приходится прибегать к упрощающим
предположениям, связанным с разбиением
пространства на дальнюю, промежуточную
и 6лижнюю области.
ставят в соответствие заданному
распределению электрических или
магнитных токов в области V
распределение полей E
и Н в пространстве. Эти операторы
являются строгими и применимы при
любых взаимных расположениях точек
источников и точек наблюдения. Однако,
идя по такому пути, как правило, не
удается получить простых замкнутых
выражений даже для сравнительно
простых излучающих систем. Потому
приходится прибегать к упрощающим
предположениям, связанным с разбиением
пространства на дальнюю, промежуточную
и 6лижнюю области.
Введём сферическую
систему координат
![]() центр которой помещен внутри излучающей
системы (рис. 18, а). Пусть точки
центр которой помещен внутри излучающей
системы (рис. 18, а). Пусть точки
![]() и Р(х, у, z) изображают соответственно
текущую точку интегрирования внутри
излучающей системы и точку наблюдения
в окружающей однородной среде. Расстояние
и Р(х, у, z) изображают соответственно
текущую точку интегрирования внутри
излучающей системы и точку наблюдения
в окружающей однородной среде. Расстояние
![]() ,
входящее в формулу (17),
равно:
,
входящее в формулу (17),
равно:
![]() (18)
(18)
где
![]() –
угол между направлениями OQ и ОР.
–
угол между направлениями OQ и ОР.
Если R>R' и точка наблюдения находится на достаточном удалении от объема с излучающими токами, то расстояние можно приближенно представить в виде ряда по степеням отношения:
![]()
Пусть
![]() ,
что соответствует наиболее важной для
теории антенн области дальнего поля
(часто называемой дальней зоной, а также
областью Фраунгофера).
,
что соответствует наиболее важной для
теории антенн области дальнего поля
(часто называемой дальней зоной, а также
областью Фраунгофера).
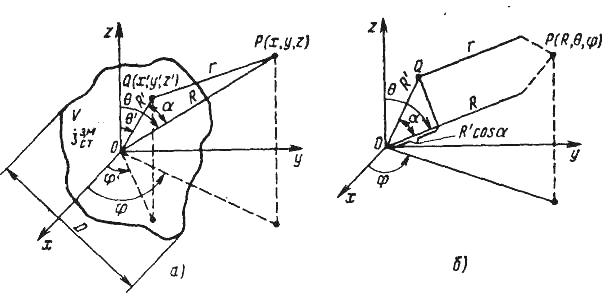
Рис. 18. К расчету электромагнитных полей излучающих систем: а — общий случай; б — точка наблюдения в дальней зоне
Тогда формула (17) упрощается:
1) в знаменателе подынтегрального выражения приближенно можно положить r=R, тогда множитель 1/R выходит из-под знака интеграла;
2) в показателе
экспоненты под интегралом можно положить
![]() ,
тогда функция
,
тогда функция
![]() также выходит из-под знака интеграла.
также выходит из-под знака интеграла.
Более аккуратный
подход к замене r
на приближенное выражение в показателе
экспоненты объясняется тем, что здесь
отбрасываемые члены должны быть малы
по сравнению с величиной
![]() ,
т. е. с периодом экспоненты с мнимым
показателем. Фактически второе
предположение означает, что лучи,
проведенные в точку наблюдения дальней
зоны из начала координат и из текущей
точки интегрирования Q, считаются
параллельными (рис. 18, б). Добавок
,
т. е. с периодом экспоненты с мнимым
показателем. Фактически второе
предположение означает, что лучи,
проведенные в точку наблюдения дальней
зоны из начала координат и из текущей
точки интегрирования Q, считаются
параллельными (рис. 18, б). Добавок
![]() к величине r
носит название разности хода лучей.
Разность хода учитывает относительное
запаздывание сферических волн, приходящих
в точку наблюдения от двух элементарных
источников, располагающихся в начале
координат и в точке Q(x', у', z').
к величине r
носит название разности хода лучей.
Разность хода учитывает относительное
запаздывание сферических волн, приходящих
в точку наблюдения от двух элементарных
источников, располагающихся в начале
координат и в точке Q(x', у', z').
Разность хода
фактически представляет собой проекцию
(рис. 18, б) вектора
![]() на направление единичного вектора,
исходящего из начала координат в точку
наблюдения:
на направление единичного вектора,
исходящего из начала координат в точку
наблюдения:
![]() (19)
(19)
Перемножая скалярно эти векторы, находим явное выражение для разности хода:
![]() (20)
(20)
Используя введенные в формулу (17) упрощения, приходим к асимптотической формуле для векторного потенциала в дальней зоне:
![]() (21)
(21)
Здесь индекс
![]() показывает, что это выражение справедливо
при
показывает, что это выражение справедливо
при
![]() .
.
Как следует из
(20), значение интеграла (21) зависит только
от угловых координат точки наблюдения
и не зависит от расстояния R. Для
перехода от векторных потенциалов
![]() к векторам полей Е и Н в дальней зоне
необходимо выполнить операции
пространственного дифференцирования.
После ряда тождественных преобразований,
а также отбрасывания членов, имеющих
радиальную зависимость
к векторам полей Е и Н в дальней зоне
необходимо выполнить операции
пространственного дифференцирования.
После ряда тождественных преобразований,
а также отбрасывания членов, имеющих
радиальную зависимость
![]() (или
(или
![]() ),
т. е. несущественных в дальней зоне,
получаем следующие расчетные
соотношения:
),
т. е. несущественных в дальней зоне,
получаем следующие расчетные
соотношения:
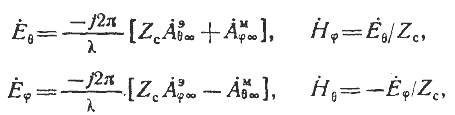 (22)
(22)
где
![]() — характеристическое сопротивление
среды. В практических расчетах вычисление
интегралов типа Удобно производить
через декартовы составляющие:
— характеристическое сопротивление
среды. В практических расчетах вычисление
интегралов типа Удобно производить
через декартовы составляющие:
![]() (23)
(23)
Переходя затем к сферическим координатам с помощью соотношений
![]() (24)
(24)
Сформулируем главные свойства электромагнитного поля излучающей системы в дальней зоне:
Поле дальней зоны имеет поперечный характер, т. е. составляющие векторов Е и Н в направлении распространения волны отсутствуют.
Поле в окрестности точки наблюдения в дальней зоне носит характер плоской электромагнитной волны, т. е. компоненты
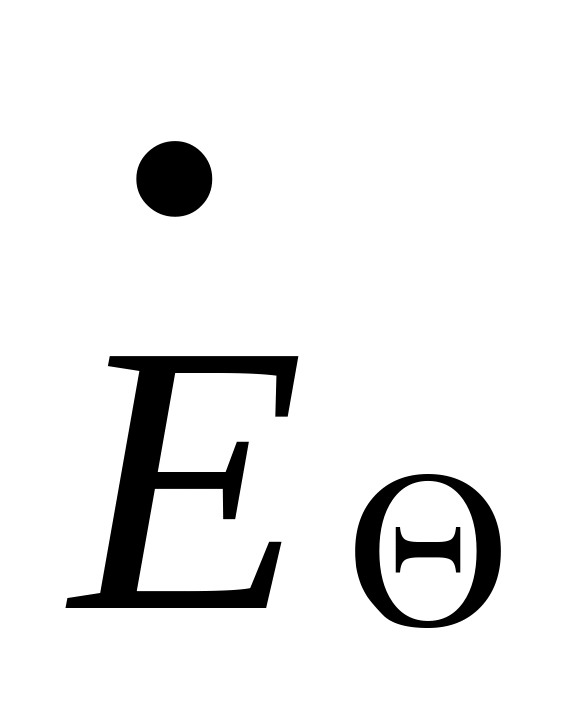 и
и
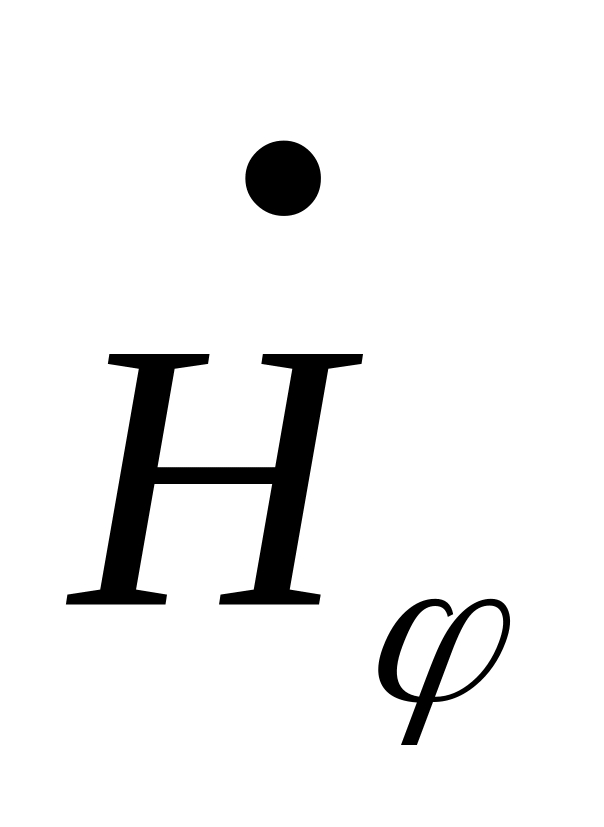 ,
а также
,
а также
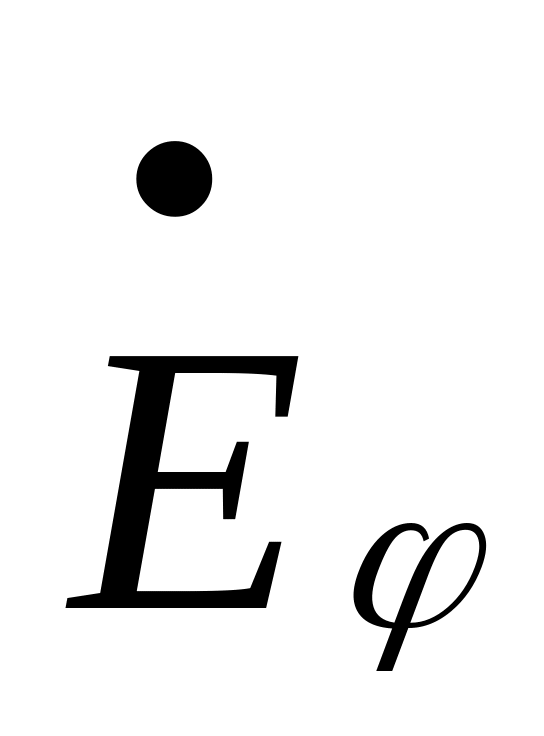 и
и
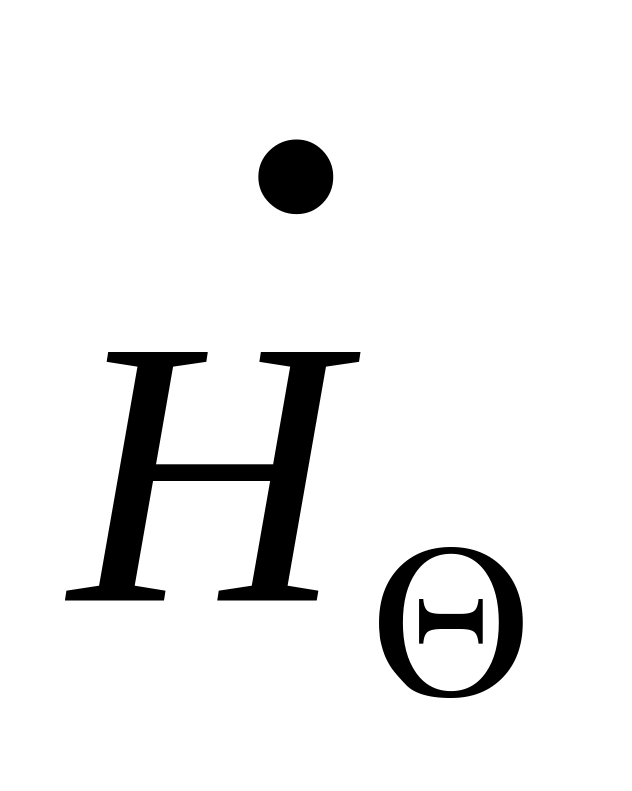 находятся в фазе и их отношение равно
характеристическому сопротивлению
среды.
находятся в фазе и их отношение равно
характеристическому сопротивлению
среды.Зависимость поля от расстояния R имеет вид расходящейся сферической волны
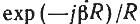 .
Однако эквифазные поверхности для
каждого компонента поля не являются в
общем случае сферами с центром в
начале координат, поскольку
.
Однако эквифазные поверхности для
каждого компонента поля не являются в
общем случае сферами с центром в
начале координат, поскольку
 и
и
 —
комплексные функции, зависящие от
углов
—
комплексные функции, зависящие от
углов
 ,
а начало координат выбрано нами
произвольно.
,
а начало координат выбрано нами
произвольно.Угловое распределение составляющих вектора Е в дальней зоне не зависит от расстояния R и может быть охарактеризовано функциями
![]() (25)
(25)
где
![]() и
и
![]() — направления максимального излучения
для соответствующих компонентов.
Функции
— направления максимального излучения
для соответствующих компонентов.
Функции
![]() и
и
![]() называются нормированными диаграммами
направленности по полю для соответствующих
составляющих.
называются нормированными диаграммами
направленности по полю для соответствующих
составляющих.
Иногда свойство 4 используют в «обращенном» виде, т. е. относят к дальней зоне те точки наблюдения, для которых угловые зависимости поперечных компонентов поля не зависят от расстояния до антенны.
5.
Поток мощности излучения в дальней зоне
всегда направлен радиально. Плотность
потока мощности равна радиальной
составляющей вектора Пойнтинга
![]() .
.
Поскольку
![]() ,
получаем
,
получаем
![]() (26)
(26)
Мнимая часть вектора Пойнтинга в дальней зоне равна нулю. Таким образом, плотность потока мощности в каждом направлений определяется как сумма независимых плотностей потоков мощности, определяемых меридиональной и азимутальной составляющими поля.
Угловая зависимость
![]() (27)
(27)
где
![]() — модуль вектора Пойнтинга в направлении
максимального излучения
— модуль вектора Пойнтинга в направлении
максимального излучения
![]() ,
называется нормированной диаграммой
направленности по мощности.
,
называется нормированной диаграммой
направленности по мощности.
Установим теперь,
на каком расстоянии от излучающей
системы можно пользоваться формулами
(21) и (22) для расчета полей, т. е. найдем
границу дальней зоны. Основное упрощение,
которое нами использовалось, заключается
в замене точного выражения
![]() приближенным
.
Возникающая из-за этого фазовая
ошибка в показателе подынтегральной
экспоненты в (17) оказывается приближенно
равной
приближенным
.
Возникающая из-за этого фазовая
ошибка в показателе подынтегральной
экспоненты в (17) оказывается приближенно
равной
![]() .
.
Так как максимальное
значение R' составляет примерно половину
наибольшего размера излучающей системы
D, то наибольшая фазовая ошибка может
составить
![]() .
Полагая допустимую фазовую ошибку
равной
.
Полагая допустимую фазовую ошибку
равной
![]() ,
после несложных преобразований
получаем искомую оценку расстояния до
ближней границы дальней зоны
,
после несложных преобразований
получаем искомую оценку расстояния до
ближней границы дальней зоны
![]() При увеличении размера излучающей
системы в длинах волн граница дальней
зоны быстро отодвигается. Если
При увеличении размера излучающей
системы в длинах волн граница дальней
зоны быстро отодвигается. Если
![]() ,
то дальняя зона начинается с расстояний
,
то дальняя зона начинается с расстояний
![]() ,
а при
,
а при
![]() начало дальней зоны соответствует
расстоянию 20 000
.
начало дальней зоны соответствует
расстоянию 20 000
.
Так как диаграммы направленности (ДН) антенн определяют угловую зависимость полей излучения именно в дальней зоне, то выполнение условия является важным требованием при экспериментальном снятии ДН с помощью пробной приемной антенны, перемещаемой по сферической поверхности вокруг исследуемой антенны.
При расстояниях дальняя зона излучающей системы плавно переходит в промежуточную область, иногда называемую областью Френеля. При расчете полей излучающих систем в промежуточной области делаются следующие упрощения:
1. Как и в случае дальней зоны, величина в знаменателе подынтегрального выражения (17) принимается приближенно равной R и выносится из-под знака интеграла.
2. В показателе
экспоненты подынтегральной функции в
(17) принимается
![]() ,
что соответствует отбрасыванию в
степенном ряду (18) членов выше второй
степени. Функция
,
не зависящая от координат источников,
выносится из-под интеграла.
,
что соответствует отбрасыванию в
степенном ряду (18) членов выше второй
степени. Функция
,
не зависящая от координат источников,
выносится из-под интеграла.
Таким образом, в промежуточной области векторные потенциалы определяются по формуле:
![]() (28)
(28)
где разность хода по-прежнему определяется формулой (20)
3. При выполнении
операций пространственного
дифференцирования отбрасываются
все члены, имеющие радиальную зависимость
![]() и
и
![]() ,
аналогично тому, как это делалось при
вычислении полей дальней зоны.
Следовательно, компоненты векторов
поля Е и Н в промежуточной области могут
быть найдены по формулам (22) с заменой
в них векторных потенциалов
,
аналогично тому, как это делалось при
вычислении полей дальней зоны.
Следовательно, компоненты векторов
поля Е и Н в промежуточной области могут
быть найдены по формулам (22) с заменой
в них векторных потенциалов
![]() на векторные потенциалы
на векторные потенциалы
![]() .
.
Сформулированные
ранее выводы о поперечном характере
дальнего поля и о его локальном подобии
плоской электромагнитной волне в
окрестности любой точки наблюдения
сохраняются и в промежуточной области.
Однако зависимость поля от расстояния
уже не имеет характера сферической
волны
![]() ,
так как расстояние R дополнительно
входит в показатель степени подынтегральной
экспоненты в (28). Расчеты показывают,
что из-за этого в промежуточной области
на монотонное убывание поля по закону
1/R накладывается осциллирующее затухающее
колебание. Угловое распределение
составляющих векторов поля оказывается
зависящим от расстояния R, т. е. ДН
излучающей системы в промежуточной
области искажаются тем сильнее, чем
меньше R. Анализ точности приближения
промежуточной зоны показывает, что
расстояние R должно находиться в пределах
,
так как расстояние R дополнительно
входит в показатель степени подынтегральной
экспоненты в (28). Расчеты показывают,
что из-за этого в промежуточной области
на монотонное убывание поля по закону
1/R накладывается осциллирующее затухающее
колебание. Угловое распределение
составляющих векторов поля оказывается
зависящим от расстояния R, т. е. ДН
излучающей системы в промежуточной
области искажаются тем сильнее, чем
меньше R. Анализ точности приближения
промежуточной зоны показывает, что
расстояние R должно находиться в пределах
![]() (29)
(29)
где D — максимальный размер излучающей системы.
Величина D/4 в левой
части неравенства играет роль только
для очень малых антенн и учитывает
амплитудную ошибку, возникающую в
связи с заменой
![]() на
на
![]() с последующим вынесением 1/R из-под знака
интеграла. При
с последующим вынесением 1/R из-под знака
интеграла. При
![]() промежуточная область охватывает
пределы
промежуточная область охватывает
пределы
![]() .
С увеличением размера антенны
промежуточная область расширяется и
при
.
С увеличением размера антенны
промежуточная область расширяется и
при
![]() охватывает расстояния от
охватывает расстояния от
![]() до
до
![]() .
Более строгое рассмотрение показывает,
что границы промежуточной и дальней
областей излучающей системы зависят
не только от расстояния R, но и от углов
наблюдения. Эти границы зависят также
от формы излучающей системы антенны и
характера распределения токов
.
Более строгое рассмотрение показывает,
что границы промежуточной и дальней
областей излучающей системы зависят
не только от расстояния R, но и от углов
наблюдения. Эти границы зависят также
от формы излучающей системы антенны и
характера распределения токов
![]()
На расстояниях, меньших нижней границы промежуточной области, располагается ближняя зона излучающей системы. В этой области электромагнитное поле имеет сложный характер и при его расчете необходимо пользоваться строгими операторами. В ближней зоне в общем случае присутствуют все компоненты поля, зависимость поля от расстояния R носит нерегулярный характер, вектор Пойнтинга становится комплексным и по направлению может не совпадать с радиусом-вектором R.
В ближней зоне излучающей системы сосредоточивается некоторый запас электромагнитной энергии, как правило, затрудняющий хорошее согласование входа антенны в широкой полосе частот.
