
- •1. Исчисление высказываний
- •1.1. Алгоритмы проверки общезначимости и противоречивости в исчислении высказываний
- •1.2. Метод резолюций в исчислении высказываний
- •1.3. Метод резолюций для хорновских дизъюнктов
- •Задачи и упражнения
- •2. Логика и исчисление предикатов
- •2.1. Логика предикатов
- •2.2. Алгебра предикатов
- •2.2.1. Логические операции
- •2.2.2. Правила записи сложных формул
- •2.2.3. Законы алгебры предикатов
- •2.2.4. Предваренная нормальная форма
- •2.2.4.1. Алгоритм приведения формулы к виду пнф
- •2.2.5. Сколемовская стандартная форма
- •2.2.5.1. Алгоритм Сколема
- •2.3. Исчисление предикатов
- •2.3.1. Интерпретация формул
- •2.3.2. Правила вывода
- •2.3.3. Метод дедуктивного вывода
- •2.3.4. Метод резолюций в исчислении предикатов
- •2.4. Проблемы в исчислении предикатов
- •2.5. Логическое программирование
- •Задачи и упражнения
- •3. Элементы теории алгоритмов
- •3.1. Рекурсивные функции
- •3.1.1. Базовые функции
- •3.1.2. Элементарные операции
- •3.2. Машина Тьюринга
- •3.2.1. Описание машины Тьюринга
- •3.2.2. Примеры машин Тьюринга
- •3.2.3. Условные обозначения и схемные соединения машин Тьюринга
- •3.2.4. Рекурсивные функции и вычисления на машинах Тьюринга
- •3.3. Конечные автоматы
- •4. Неклассические логики
- •4.1. Пропозиционные логики
- •4.2. Алгоритмические логики
- •Задачи и упражнения
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.3. Метод резолюций для хорновских дизъюнктов
В общем случае метод резолюций неэффективен, так как количество переборов, которые необходимо сделать для получения ответа, экспоненциально зависит от количества информации (числа дизъюнктов и переменных), содержащейся в множестве дизъюнктов. Однако для некоторых классов дизъюнктов, к которым относится класс хорновских дизъюнктов, метод резолюций эффективен.
Дизъюнкт D называется хорновским, если он содержит не более одной переменной без отрицания (позитивной переменной).
Пример. Хорновскими
дизъюнктами являются следующие дизъюнкты:
![]() ,
,
![]() ,
,
В.
,
,
В.
В общем случае
хорновские дизъюнкты имеют вид
![]() (что равносильно формуле
(что равносильно формуле
![]() )
или
)
или
![]() .
Хорновский дизъюнкт вида
называется точным. При этом переменные
А1, …, Аn
называются фактами, а переменная В
– целью. Хорновский дизъюнкт вида
называется негативным. Дизъюнкт D=B
называется унитарным позитивным
дизъюнктом.
.
Хорновский дизъюнкт вида
называется точным. При этом переменные
А1, …, Аn
называются фактами, а переменная В
– целью. Хорновский дизъюнкт вида
называется негативным. Дизъюнкт D=B
называется унитарным позитивным
дизъюнктом.
Если S
– множество хорновских дизъюнктов, то
невыполнение множества S
проверяется следующим образом. Выбирается
в S унитарный позитивный
дизъюнкт Р и дизъюнкт D
из S, содержащий
![]() .
После этого заменяем S
на (S \
{D}){res(D,P)}
и продолжаем процесс до тех пор, пока S
не будет содержать 0. Если на заключительном
шаге множество дизъюнктов будет содержать
0, то исходное множество S противоречиво,
в противном случае S непротиворечиво.
.
После этого заменяем S
на (S \
{D}){res(D,P)}
и продолжаем процесс до тех пор, пока S
не будет содержать 0. Если на заключительном
шаге множество дизъюнктов будет содержать
0, то исходное множество S противоречиво,
в противном случае S непротиворечиво.
Пример. Проверить на противоречивость множество дизъюнктов
![]() .
.
Для доказательства противоречивости запишем дизъюнкты из S в таблицу и применим описанные алгоритм, записывая результат каждого следующего шага в таблицу. Переменные, использующиеся на данном шаге, будем подчеркивать.
Номер шага |
|
|
R |
|
|
|
1 |
|
Q |
R |
|
T |
|
2 |
|
Q |
R |
|
T |
|
3 |
P |
Q |
R |
|
T |
|
4 |
|
|
|
|
|
0 |
На шаге 4 получаем 0, являющийся резолютивным выводом из S. Следовательно, множество S невыполнимо.
Задачи и упражнения
1. Выполнить подстановку:
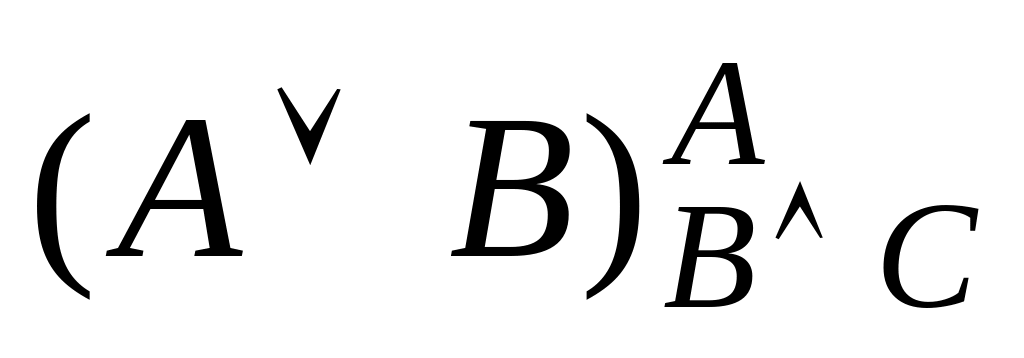 ;
;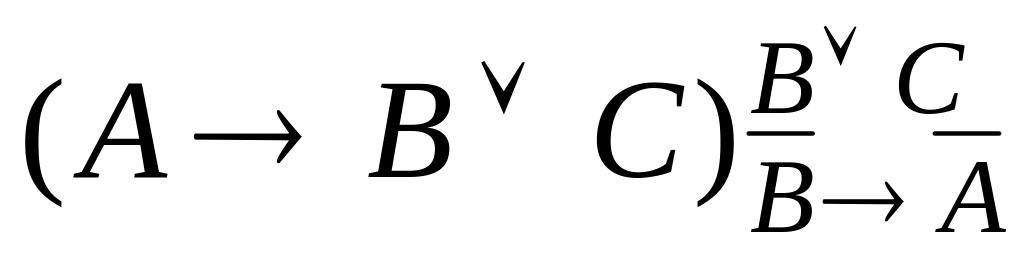 ;
;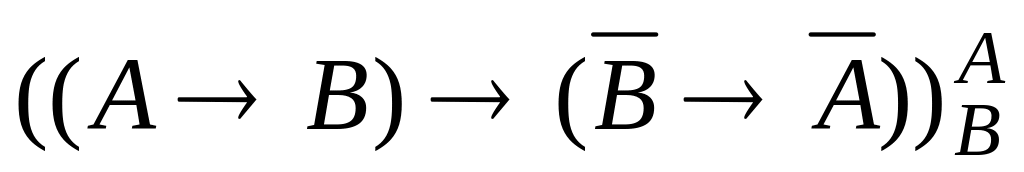 .
.
Доказать выводимость в исчислении высказываний:
а)
![]() ├─
├─![]() ;
;
б)
![]() ├─
├─![]()
в)
├─![]()
г)
![]() ├─
├─![]()
д)
├─![]()
е)
├─![]() .
.
Выводимы ли в исчислении высказываний следующие формулы:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
С помощью алгоритма Квайна и алгоритма редукции доказать тождественную истинности аксиом исчисления высказываний.
5. Проверить на противоречивость множество хорновских дизъюнктов
S={![]() }.
}.
6. Выводимость заключения по методу резолюции:
а)
![]()
б)
![]()
в)
![]()
2. Логика и исчисление предикатов
В логике высказываний в качестве исходных элементов рассматриваются некоторые элементарные высказывания, из которых строятся более сложные высказывания, называемые формулами. При этом не анализируется структура и состав высказываний, а учитываются лишь значения истины или лжи, которые они могут принимать. Однако есть много рассуждений, которые не могут быть рассмотрены таким простым способом. Например, приведем следующее умозаключение:
Каждый человек смертен.
Сократ – человек, следовательно, он смертен.
Очевидно, рассмотренное рассуждение интуитивно корректно. Однако, введя следующие обозначения:
A=«Каждый человек смертен»,
B= «Сократ – человек»,
C=«Сократ смертен»,
получаем
формулу
![]() ,
которая не доказуема в исчислении
высказываний. Указанное несоответствие
между утверждениями имеет место потому,
что в логике высказываний не используется
структура высказываний A,
B
и С. В этом разделе введем логику
предикатов (логику первого порядка) и
исчисление предикатов, которые позволяют
преодолеть подобные трудности и дают
возможность проверить формализацию
большей части повседневного и
математического языка.
,
которая не доказуема в исчислении
высказываний. Указанное несоответствие
между утверждениями имеет место потому,
что в логике высказываний не используется
структура высказываний A,
B
и С. В этом разделе введем логику
предикатов (логику первого порядка) и
исчисление предикатов, которые позволяют
преодолеть подобные трудности и дают
возможность проверить формализацию
большей части повседневного и
математического языка.
