
- •1. Исчисление высказываний
- •1.1. Алгоритмы проверки общезначимости и противоречивости в исчислении высказываний
- •1.2. Метод резолюций в исчислении высказываний
- •1.3. Метод резолюций для хорновских дизъюнктов
- •Задачи и упражнения
- •2. Логика и исчисление предикатов
- •2.1. Логика предикатов
- •2.2. Алгебра предикатов
- •2.2.1. Логические операции
- •2.2.2. Правила записи сложных формул
- •2.2.3. Законы алгебры предикатов
- •2.2.4. Предваренная нормальная форма
- •2.2.4.1. Алгоритм приведения формулы к виду пнф
- •2.2.5. Сколемовская стандартная форма
- •2.2.5.1. Алгоритм Сколема
- •2.3. Исчисление предикатов
- •2.3.1. Интерпретация формул
- •2.3.2. Правила вывода
- •2.3.3. Метод дедуктивного вывода
- •2.3.4. Метод резолюций в исчислении предикатов
- •2.4. Проблемы в исчислении предикатов
- •2.5. Логическое программирование
- •Задачи и упражнения
- •3. Элементы теории алгоритмов
- •3.1. Рекурсивные функции
- •3.1.1. Базовые функции
- •3.1.2. Элементарные операции
- •3.2. Машина Тьюринга
- •3.2.1. Описание машины Тьюринга
- •3.2.2. Примеры машин Тьюринга
- •3.2.3. Условные обозначения и схемные соединения машин Тьюринга
- •3.2.4. Рекурсивные функции и вычисления на машинах Тьюринга
- •3.3. Конечные автоматы
- •4. Неклассические логики
- •4.1. Пропозиционные логики
- •4.2. Алгоритмические логики
- •Задачи и упражнения
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.1. Алгоритмы проверки общезначимости и противоречивости в исчислении высказываний
1. Алгоритм
Квайна. Напомним, что формула F
от пропозициональных переменных А1,
А2, …, Аn
является тождественно истинной или
(что то же самой) доказуемой, если булева
функция
![]() ,
соответствующая формуле F,
тождественно равна 1. Для проверки
значений функции f
используется так называемое семантическое
дерево, т.е. бинарное дерево, которое
удовлетворяется следующим условиям:
,
соответствующая формуле F,
тождественно равна 1. Для проверки
значений функции f
используется так называемое семантическое
дерево, т.е. бинарное дерево, которое
удовлетворяется следующим условиям:
каждое ребро соответствует переменной (с отрицанием или без);
ребра, выходящие из одной вершины, соответствуют контрарным переменным:
 ,
,
 ;
;ребра соответствуют одной и той же переменной тогда и только тогда, когда они находятся на одинаковом расстоянии от корня (рис. 1.1).
Семантическое
дерево имеет
![]() висячих вершин и для проверки общезначимости
необходимо пройти
маршрутов от корня до этих вершин.
висячих вершин и для проверки общезначимости
необходимо пройти
маршрутов от корня до этих вершин.
Алгоритм Квайна позволяет проходить не все семантическое дерево, а только его часть. Он состоит в том, что пропозициональным переменным , упорядоченным в набор (А1, А2, …, Аn), последовательно придают значения 0 и 1 и анализируют таблицы истинности формул, содержащих меньшее число переменных.

Пример. Проверить общезначимость формулы
![]() .
.
Упорядочим пропозициональные переменные (А, В, С). Придадим первой переменной А значение 1, т.е. А=1. Тогда формула F преобразуется следующим образом:
![]()
![]() .
.
В полученной
формуле переменной В придадим
значение 1, т.е. В=1. Тогда преобразованная
формула имеет вид
![]() ,
т.е. будет общезначимой. В случае В=0
имеем
,
т.е. будет общезначимой. В случае В=0
имеем
![]() ,
что также общезначимо. Рассмотрим теперь
случай А=0. Имеем
,
что также общезначимо. Рассмотрим теперь
случай А=0. Имеем
![]() .
.
Таким образом, все возможные случаи приводят к тождественно истинным формулам. Следовательно, формула F также истинна. На рис. 1.2а изображено семантическое дерево, соответствующее формуле F, а на рис. 1.2б показана часть семантического дерева, которая фактически использовалась для проверки общезначимости.
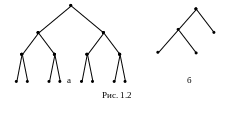
2. Алгоритм редукции решает ту же задачу проверки общезначимости формулы, но используется в том случае, когда в формуле содержится достаточно много импликаций. Идея алгоритма состоит в попытке нахождения значений пропозициональных переменных формулы F, при которых значение функции f равно 0, на основе того, что импликация является ложной в том и только в том случае, когда посылка истинна, а заключение ложно.
Пример. Проверить тождественную истинность формулы
![]()
Предположим, что
формула ложна при некотором наборе
значений переменных А, В, С.
Тогда истинностная функция f
по этим значениям переменных дает
следующие значения формул:
![]() ,
,
![]() .
Тогда из второго равенства получает
А=1,
.
Тогда из второго равенства получает
А=1,
![]() ,
откуда имеем B=1, C=0.
Однако при этих значениях справедливо
,
откуда имеем B=1, C=0.
Однако при этих значениях справедливо
![]() .
Получили противоречие. Таким образом,
формула F
тождественно истинна.
.
Получили противоречие. Таким образом,
формула F
тождественно истинна.
1.2. Метод резолюций в исчислении высказываний
Пусть
![]() и
и
![]() – дизъюнкты. Дизъюнкт
– дизъюнкты. Дизъюнкт
![]() называется резольвентой дизъюнктов
D1 и D2
по переменной А и обозначается через
resA(D1,D2).
Резольвентой дизъюнктов D1
и D2 называется
резольвента по некоторой переменной и
обозначается через res(D1,D2),
res(A,
)=0.
Если дизъюнкты D1
и D2 не содержат
контрарных переменных, то резольвент
у них не существует.
называется резольвентой дизъюнктов
D1 и D2
по переменной А и обозначается через
resA(D1,D2).
Резольвентой дизъюнктов D1
и D2 называется
резольвента по некоторой переменной и
обозначается через res(D1,D2),
res(A,
)=0.
Если дизъюнкты D1
и D2 не содержат
контрарных переменных, то резольвент
у них не существует.
Пример. Если
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() не существует.
не существует.
Утверждение. Если
![]() существует, то
существует, то
![]() ├─
.
├─
.
Пусть
![]() – множество дизъюнктов. Последовательность
формул
– множество дизъюнктов. Последовательность
формул
![]() называется резолютивным выводом из S,
если для каждой формулы
называется резолютивным выводом из S,
если для каждой формулы
![]() (i=1,…,n)
выполняется одно из условий:
(i=1,…,n)
выполняется одно из условий:
1)
![]() ;
;
2) существуют
![]() такие, что
такие, что
![]() .
.
Теорема (о полноте метода резолюций). Множество дизъюнктов S противоречиво в том и только в том случае, когда существует резолютивный вывод из S, заканчивающийся 0.
Существует эффективный метод логического вывода – метод резолюции. Он основан на том, что выводимость формулы В из множества посылок F1, F2, F3, …, Fn равносильна доказательству теоремы
├─ (F1F2F3. . . FnB),
формулу которой можно преобразовать так:
├─ (F1F2F3. . . FnB)
├─ (![]() B)
B)
├─
![]() .
.
Следовательно,
заключение В истинно тогда и только
тогда, когда формула F1F2F3.
. . Fn
![]() 0.
Это возможно при значении 0 хотя бы
одной из подформул Fi
или
.
0.
Это возможно при значении 0 хотя бы
одной из подформул Fi
или
.
Для анализа этой формулы все подформулы Fi и должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные атомы) формируют третий дизъюнкт – резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустую резольвенту. Наличие пустого дизъюнкта свидетельствует о выполнении условия
F1F2F3. . . Fn 0.
Опишем пошагово алгоритм вывод по методу резолюций.
Шаг 1. Придать отрицание заключению, т.е. .
Шаг 2. Привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме.
Шаг 3. Выписать множество дизъюнктов всех посылок и отрицания заключения S = {D1, D2, …, Dk }.
Шаг 4. Выполнить анализ пар множества S по правилу:
«если существуют дизъюнкты Di и Dj, один из которых (Di) содержит переменную А, а другой (Dj) – контрарную переменную , то соединить эту пару логической связкой дизъюнкции (DiDj) и сформировать новый дизъюнкт – резольвенту, исключив контрарные литеры А и ».
Шаг 5. Если в результате соединения дизъюнктов, содержащих контрарные переменные, будет получена пустая резольвента – 0, то конец, в противном случае включить резольвенту в множество дизъюнктов S и перейти к шагу 4.
Примеры.
1. Работа автоматического устройства, имеющего три клапана А, В и С, удовлетворяет следующим условиям: если не срабатывают клапаны А или В или оба вместе, то срабатывает клапан С; если срабатывают клапаны А или В или оба вместе, то не срабатывает клапан С. Следовательно, если срабатывает клапан С, то не срабатывает клапан А.
![]()
1)
![]() – посылка;
– посылка;
2)
![]() – посылка;
– посылка;
3)
![]() – отрицание заключения;
– отрицание заключения;
4) множество
дизъюнктов: S={(АC),
(BC),
![]() ,
,
![]() ,
C, А}.
,
C, А}.
Построим резолютивный вывод, заканчивающийся 0.
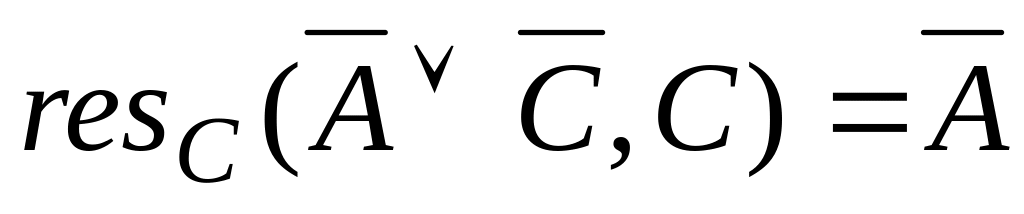 .
.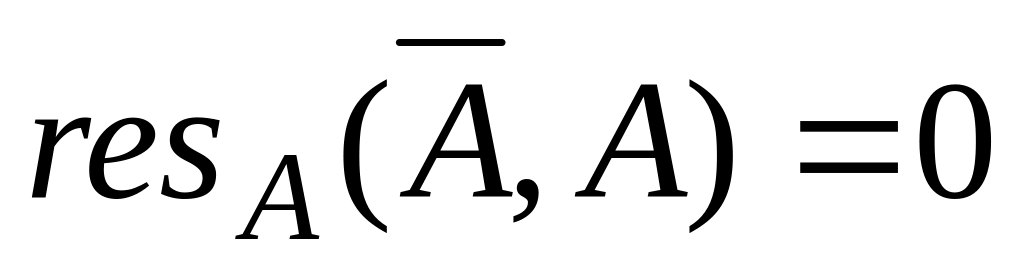 .
.
Так доказано, что если срабатывает клапан С, то не срабатывает клапан А.
2. Доказать истинность заключения
![]()
1) A – посылка;
2) B – посылка;
3)
![]() – посылка;
– посылка;
4)
![]() – отрицание заключения;
– отрицание заключения;
5)
множество дизъюнктов:
S={A,
B, (![]() ),
C};
),
C};
6)
![]() ;
;
7) S1={A,
B, (
),
C, (![]() )};
)};
8)
![]() ;
;
9) S2={A,
B, (
),
C, (
),![]() };
};
10)
![]() – пустая резольвента.
– пустая резольвента.
Так доказана истинность заключения по принципу резолюции.
Для иллюстрации вывода удобно использовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а концевыми вершинами ветвей – оставшиеся дизъюнкты отрицания заключения и всех посылок. Узлами графа типа дерево являются резольвенты. Ниже дан пример, сопровождаемый графом.
Пример. Доказать истинность заключения
![]()
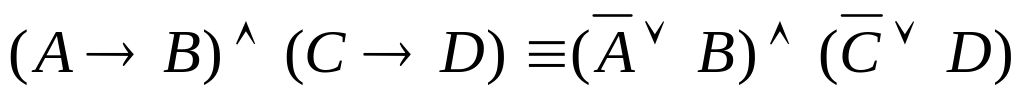 –
посылка;
–
посылка;
2)
![]() – посылка;
– посылка;
3)
![]() –
посылка;
–
посылка;
4)
![]() – отрицание заключения;
– отрицание заключения;
5) S
={A,
C,
,
![]() ,
,
![]() ,
,
![]() }
}
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9 )
)
![]() ;
;
10)
![]() – пустая резольвента.
– пустая резольвента.
Так доказана истинность заключения , граф доказательства изображен на рис.1.3.

Замечание. Метод резолюций достаточен для обнаружения возможной выполнимости данного множества – дизъюнктов S. Для этого включим в S все дизъюнкты, получающиеся при резолютивном выводе из S. Из теоремы о полноте метода резолюций вытекает
Следствие. Если множество дизъюнктов S содержит резольвенты всех своих элементов, то S выполнимо тогда и только тогда, когда 0S.
Двойственным к
правилу резолюций является правило
согласия. Пусть
![]() ,
,
![]() – конъюнкты. Положим
– конъюнкты. Положим
![]() ,
,
![]() .
.
Пусть
![]() – множество конъюнктов. Последовательность
формул
называется выводом из S
по правилу согласия, если для каждой
формулы
(i=1,…,n)
выполняется одно из условий:
– множество конъюнктов. Последовательность
формул
называется выводом из S
по правилу согласия, если для каждой
формулы
(i=1,…,n)
выполняется одно из условий:
1) ;
2) существуют
такие, что
![]() .
.
Теорема. Множество конъюнктов общезначимо (т. е. выполняется) тогда и только тогда, когда существует вывод из S по правилу согласия, заканчивающийся символом 1.
