3.2.1. Описание машины Тьюринга

Математическая модель машины Тьюринга имеет вид:

Т = < v_t; Q; D; ; ;  >,

где: VT = {ai; a2; ... an}	– множество символов алфавита внешней памяти;
Q = {qi; q2; ... qm}	– множество символов алфавита внутренней памяти;
D = {П; Л; С}	– множество символов алфавита перемещения головки;
: Q  vt => vt	– функция выхода машины Тьюринга;
: Q  vt => vt	– функция переходов машины Тьюринга.
: Q  vt => vt	– функция перемещения головки машины Тьюринга.

С алгебраической точки зрения машина Тьюринга является трехосновной алгеброй, т. е. алгеброй с тремя множествами (внешней памяти, внутренней памяти и перемещения головки) и тремя функциями (выхода, переходов и перемещений).

Полное описание машины Тьюринга определяется полной записью всех слов на информационной ленте, положением головки относительно ячеек информационной ленты и текущим состоянием управляющего устройства. Такое описание называют конфигурацией машины Тьюринга и обозначают

K =  q_i , где  – слово, расположенное слева от головки;

 – слово, расположенное вправо от головки;

q_i – текущее состояние машины Тьюринга.

Введенное понятие «состояние» машины Тьюринга определяет ее «память», т. е. учет всех тех конфигураций, которые привели машину в текущее q_i состояние. Следует обратить внимание, что символ, находящийся в ячейке под считывающей головкой, является первым символом слова , т.е.

 = (a_j ).

Каждая конфигурация содержит только одно вхождение символа q_i. К незаключительной конфигурации может быть применима только одна команда, которая переводит машину в новую конфигурацию. Так реализуется дискретность и детерминированность алгоритмического процесса.

Для удобства анализа вычислительных алгоритмов рекурсивных функций математик Пост предложил ограничить множество символов внешнего алфавита v_t двумя символами, т.е. v_t = {|; #}, где "|" (палочка) есть символ унарного кода числа, а "#" – символ пробела между числами. При этом любое целое положительное число может быть представлено на информационной ленте последовательностью палочек, как это представлено в табл. 2.

Таблица 2

Число в десятичной системе счисления	«Слово» в унарном коде на информационной ленте
0	|
1	||
2	|||
3	||||
........................	..........................................
i

«x» эквивалентно « | ^{x + 1}»

Для упорядочения составления протоколов машины Тьюринга информационную ленту ограничивают полулентой бесконечной длины только в одну сторону. Алгоритмы допустимо исследовать на левой полуленте бесконечной в левую сторону и правой полуленте бесконечной в правую сторону. В зависимости от используемой полуленты приняты различные схемы записи стандартных конфигураций машины Тьюринга (табл. 3).

Таблица 3

Стандартная	Информационная полулента
конфигурация	правая	левая
Началь-ная	qí | x 1+ 1# | x 2+ 1 # ... #| x n+ 1	| x 1+ 1# | x 2+ 1 # ... #| x n qí |
Конечная	qk | y + 1	| y qk |

Работу машины Тьюринга удобно представлять протоколом, таблицей и графом.

При протокольной записи все команды должны быть записаны упорядоченным списком. Например,

1) q_ía_i  q_ia_jD

2) q_i a_k  q_j a_iD

.................................

n) q_| a_m  q_k a_n C.

При табличном представлении строки описывают текущее состояние машины, а столбцы – содержимое обозреваемой ячейки. Тогда элементами матрицы этой таблицы являются правые части команд (q_ja_iD) для соответствующей пары текущего состояния машины (q_iа_к). Табличная форма описания машины более компактна и позволяет применить матричные методы анализа для оптимизации структуры алгоритма (табл. 4).

Таблица 4

Текущее	Символы vt
состояние	аi	ак	...	am
qн	qiajD	...
qi	...	qjaiD		...
...	...	...	...	...
qk	...	...	...	qkanC

При графовом представлении вершинам графа соответствуют состояния машины, а дугам – переходы в те состояния, которые предусмотрены командой. При этом на дуге указывают считываемый сигнал обозреваемой ячейки / записываемый сигнал в обозреваемую ячейку и команда на перемещение головки (рис. 3.1). Граф машины Тьюринга, реализующей заданный алгоритм, часто называют граф-схемой алгоритма (ГСА).

q_i q_|

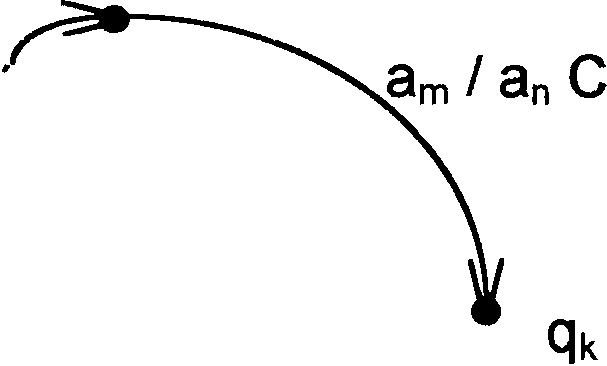
Рис. 3.1. Граф-схема алгоритма

Граф-схема алгоритма обеспечивает наглядность и позволяет применять различные методы исследования графов для оптимизации структуры алгоритма.