ФГБОУ ВПО “Воронежский государственный
технический университет”
СПРАВОЧНИК МАГНИТНОГО ДИСКА
(кафедра высшей математики и
физико-математического моделирования)
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
Методические указания
для проведения тестовых и контрольных работ
у студентов направления 230400.62
«Информационные системы и технологии»
по дисциплине «Математика»
Часть 5
Составители: Марина Леонидовна Лапшина
Марина Владимировна Юрьева
Метод. указ. Ч.5.doc 1,91 Мбайт 20.11.2013 3,1 уч.-изд.л.
(наименование файла) (объём файла) (дата) (объём издания)
ФГБОУ ВПО “Воронежский государственный
технический университет”
Кафедра высшей математики и физико-математического
моделирования
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
Методические указания
для проведения тестовых и контрольных работ
у студентов направления 230400.62
«Информационные системы и технологии»
по дисциплине «Математика»
Часть 5
Воронеж 2013
Составители: д-р техн. наук М.Л. Лапшина,
канд. физ.- мат. наук М.В. Юрьева
УДК 517.2 (07)
Контрольно-измерительные материалы: методические указания для проведения тестовых и контрольных работ у студентов направления 230400.62 «Информационные системы и технологии» по дисциплине «Математика». Ч.5/ ФГБОУ ВПО «Воронежский государственный технический университет»; сост.: М.Л. Лапшина, М.В. Юрьева. Воронеж, 2013. 51 с.
Методические указания предназначены для проведения практических занятий по теме «Теория поля». Для каждого практического занятия приводятся необходимые теоретические сведения и формулы, примеры решения задач, а также задачи для самостоятельного решения. Приведены задания для проведения тестовых и контрольных работ
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Метод. указ. Ч.5.doc.
Ил. 3. Библиогр.: 4 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Горбунов
Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО “Воронежский государственный
технический университет”, 2013
Вопросы для самопроверки
1. Понятие поля. Виды полей.
2. Скалярное поле. Линии и поверхности уровня.
3. Производная по направлению.
4. Формулы для вычисления производной по направлению для двумерного и трехмерного поля.
5. Градиент, его свойства.
6. Векторное поле. Векторные линии.
7. Поток векторного поля через поверхность, его физический смысл.
8. Формула Остроградского.
9. Дивергенция векторного поля, ее физический смысл.
10. Линейный интеграл в векторном поле, его свойства и физический смысл.
11. Циркуляция векторного поля. Формула Стокса.
12. Ротор векторного поля, его физический смысл.
13. Условия независимости линейного интеграла от формы пути интегрирования.
14. Потенциальное поле. Условия потенциальности.
15. Нахождение потенциала.
16. Соленоидальные и гармонические поля.
17. Оператор Гамильтона, Векторные операции второго порядка.
Практические занятия
Перед каждым практическим занятием необходимо прочитать по лекциям и учебнику соответствующий материал и ответить на вопросы, относящиеся к теме занятия.
Понятие поля лежит в основе многих представлений современного естествознания. Средством изучения полей является векторный анализ.
Если в каждой точке некоторой области
в каждый момент времени t
задано значение некоторой физической
величины
=
(М,
t), то эта область
называется полем величины
.
Если поле величина
не зависит от времени (
=
(м)),
то оно называется стационарным
При рассмотрении физических явлений встречаются величины трёх типов: скалярные, векторные, тензорные. Соответственно различают три типа полей. Мы будем рассматривать скалярные и векторные стационарные поля.
Если в пространственной области D задана скалярная функция точки u=u(x,y,z), то поле – скалярное. Примерами скалярных полей могут служить поле температур в точках какого-либо тела, поле электрического потенциала, давления газа и т.д.
Если в области D задана
вектор-функция
,
то поле – векторное. Примерами векторных
полей являются поле скоростей точек
движущейся жидкости, поле силы тяжести
электромагнитное поле и т.д.
(Могут рассматриваться области в пространстве двух, трех или n измерений).
Изучение скалярных поле производится методами дифференциального исчисления функций двух и трёх переменных (производная по направлению, градиент, поверхности и линии уровня.). Для изучения векторных полей применяется интегральное исчислении функции нескольких переменных.
Занятие 1. Линии и поверхности уровня. Производная по направлению. Градиент
Простейшими геометрическими характеристиками скалярных полей являются линии уровня u(x, y)=C в пространстве двух измерений и поверхности уровня u(x, y, z)=C в пространстве трех измерений.
По определению производная скалярного поля для трехмерного случая:
,
где
.
Пусть единичный вектор данного направления
вектор
задан координатами:
.
Производная по направлению
вычисляется по формуле
(1)
Аналогично определяется производная в данном направлении для функции двух переменных. В этом случае
т.к. (
).
(2)
Градиентом скалярного поля u(P), обозначаемым grad u называется вектор, проекциями которого являются частные производные функции u(P) по соответствующим координатам
.
(3)
Аналогично определяется градиент функции двух переменных u=f(x,y). Это – вектор на плоскости Oxy:
(4)
Модуль градиента равен наибольшей скорости возрастания функции в данной точке
.
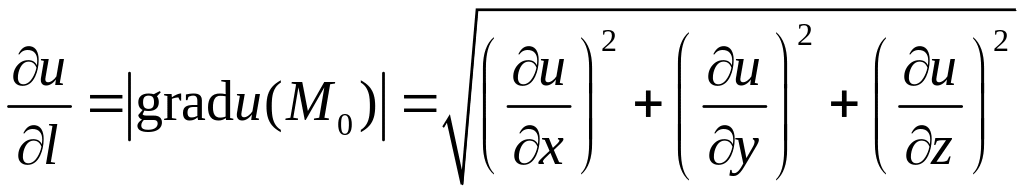(5)
Пример 1, Найти производную поля
в точке P(1;0) в направлении,
составляющем с осью Ox
угол 1200.
Решение. Находим частные производные данной функции и их значения в точке P:
Так
как
,
то по формуле (2) получим
.
Знак минус указывает, что функция в
данной точке и в данном направлении
убывает.
Пример 2. Найти производную поля f(x,y,z)=xy2z в точке М0(5,1,2) по направлению к точке М1(9,4,14).
Решение. Находим направляющие косинусы
вектора
:
=
;
.
Найдем значения частных производных в точке М0
.
По формуле (1) получим:
.
Положительный знак указывает, что функция в данной точке и в данном направлении возрастает.
Пример 3. Найти градиент поля
в точке P(1;1).
Решение. Находим частные производные
и их значения в точке P:
С
Следовательно,
.
Задачи для самостоятельного решения:
1. Определить вид линий или поверхностей уровня следующих скалярных полей:
1.
.
Ответ: линии уровня – параболы
y2=C – x.
2. u=xy. Ответ: линии уровня – гиперболы
xy=C. (при C=0 – совокупность координатных осей).
3.
.
Ответ: линии уровня – прямые
y=Cx.
4. u=x+y+z. Ответ: Поверхности уровня – параллельные плоскости x+y+z=C.
5.
. Ответ: Поверхности уровня – однопо-
лостные и двуполостные гиперболоиды
(при С=0 – конус
)
6.
.
Ответ: Поверхности уровня – парабо-
лоиды вращения
.
II. Исходя из выражения для производной по направлению и определения градиента, доказать следующие свойства градиента:
1. Производная поля по направлению s
равна скалярному произведению
градиента поля на единичный вектор
данного направления, т. е. равна проекции
градиента на данное направление
,
где
- угол между градиентом и вектором
.
2. Направление градиента есть направление наискорейшего возрастания функции поля.
3. В каждой точке поля градиент направлен
по нормали к соответствующей поверхности
уровня в сторону возрастания потенциала
поля. т. е.
,
где n – нормаль к
поверхности уровня, направленная в
сторону возрастания функции поля.
III.Найти производную от следующих полей в заданных точках по заданному направлению:
1.
в точке P0(2, -1) по
направлению P0P1,
где P1(0,2).
Ответ: 13/5.
2.
в точке P0(2,1,1) по
направлению прямой
в сторону возрастания поля.
Ответ:
.
3. Найти угол между градиентами поля
в точках P1(2,3,1),
P2(1,-1,2).
Ответ:
.
4. Найти скорость и направление наибыстрейшего возрастания поля u=xyz в точке P0(1,2,-2).
Ответ:
.
5. Найти единичный вектор нормали к
поверхности уровня поля
в точке P0(1, 1, -1),
направленный в сторону возрастания
поля.
Ответ:
.
6. Найти стационарные точки поля
Ответ: P(3,3,-3).
8. Убедиться в ортогональности линий уровня полей:
а)
,
;
б)
;
9. Убедиться в ортогональности поверхностей уровня следующих полей:
а)
,
;
б)
,
;
в)
,
,
.
10. Найти семейство линий наибыстрейшего возрастания для следующих полей:
а) плоского поля ;
б) трехмерного поля
;
в) трехмерного поля .
Ответ: а)
,
б)
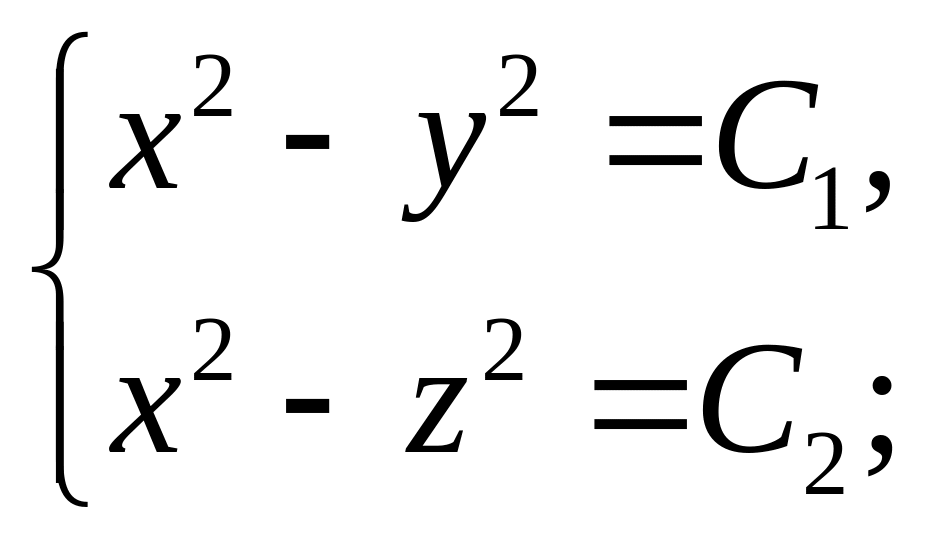в)
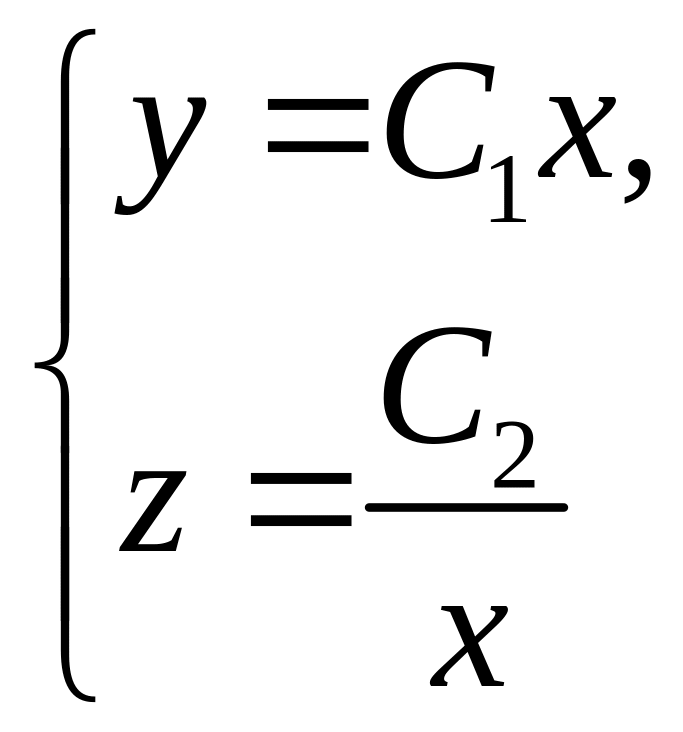
Занятие 2. Векторные линии. Дивергенция. Ротор
Векторной линией поля
называется линия, в каждой точке которой
касательная имеет направление вектора
,
соответствующего этой точке.
Векторные линии для вектора определяются системой дифференциальных уравнений
(6)
(аналогично для плоских и многомерных полей).
Дивергенцией векторного поля называется скалярная функция
.
(7)
Ротором (вихрем) векторного поля называется вектор
(8)
или
.
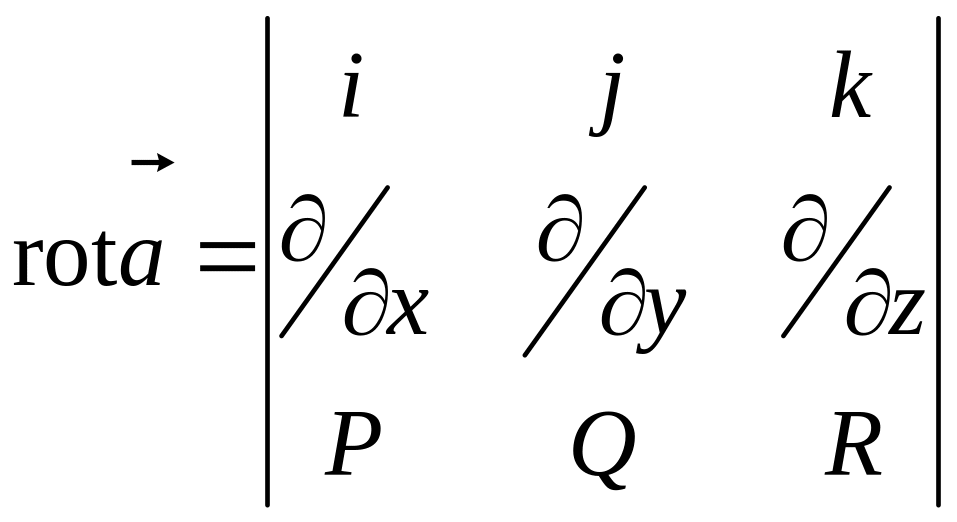(9)
В случае плоских полей функции u, P, Q зависят лишь от двух переменных, а функция R тождественно равна нулю.
Пример 1. Найти уравнения векторных линий поля
Решение. Здесь область D
– все пространство, за исключением
точки O(0,0,0). Система
(6) в этом случае имеет вид:
.
Перепишем ее в виде
Отсюда следует:
и
,
то есть
.
Точка O является особой
точкой для системы (6). Характер этой
особенности виден из последнего
полученного уравнения (если
):
если
то
.
Пример 2. Найти дивергенцию и ротор векторного поля
.
Решение. Здесь
;
по формуле(7), т.к.
,
имеем:
.
Для нахождения ротора воспользуемся
формулой (9):
=
.
Задачи для самостоятельного решения:
I. Найти векторные линии следующих полей:
1.
.
Ответ: Окружности -
.
2.
.
Ответ: Гиперболы xy=C. (при C=0 – совокупность координатных осей).
3.
.
Ответ: Параболы y2= 2(C +x).
4.
.
Ответ: Прямые
.
5.
(
– постоянный вектор).
Ответ: Окружности, являющиеся сечениями
сфер
плоскостями
,
перпендикулярными вектору
.
6.
.
Ответ: Линии пересечения гиперболических
цилиндров
с такими же цилиндрами
.
7.
.
Ответ: Окружности, являющиеся линиями
пересечения сфер
с
плоскостями
.
II. Найти а) дивергенцию б) ротор векторного поля:
1.
Ответ: а) 7+9π, б) 0.
2.
.
Ответ: а) 18π-1, б) 0.
3.
.
Ответ: а) 2z+1, б)
.
4.
.
Ответ: а) 81π-1,б) 0.
5.
.
Ответ: а) 4z, б)
.
6.
.
Ответ: а) 11π+2, б)0.
7.
.
Ответ: а)
б)
8.
.
Ответ: а)
,
б)
.
Занятие 3. Работа силового поля. Линейный интеграл
Пусть на дуге
кусочно-гладкой кривой задано поле
.
Делим дугу
на
произвольных частей с длинами
.
Наибольшую из них обозначаем через
.Тогда
на элементе дуги
работа поля приближенно равна
,
а вся работа
,
где
-
некоторая точка элемента
.
Переходя к пределу при
,
получим точное значение работы (если
предел существует) при перемещении в
силовом поле материальной точки по дуге
из точки A в точку B:
=
Это – криволинейный интеграл 2-го рода.
В теории поля его называют линейным
интегралом. Аналогично определяются
линейные интегралы в плоских и многомерных
векторных полях. Пусть кривая AB
задается параметрическими уравнениями:
.
Тогда
.
(10)
Здесь t0 и T – значения параметра t, отвечающие точкам A и B.
Линейный интеграл вектора
,
взятый по замкнутому контуру C,
называется циркуляцией вектора поля
по данному контуру и обозначается
символом
.
Направление обхода контура указывается
заранее. Положительным считается обход
против часовой стрелки, а отрицательным
– по часовой стрелке.
Для плоских векторных полей имеет место следующее утверждение:
Если векторная функция
непрерывна вместе с производными
и
в замкнутой области
,
то
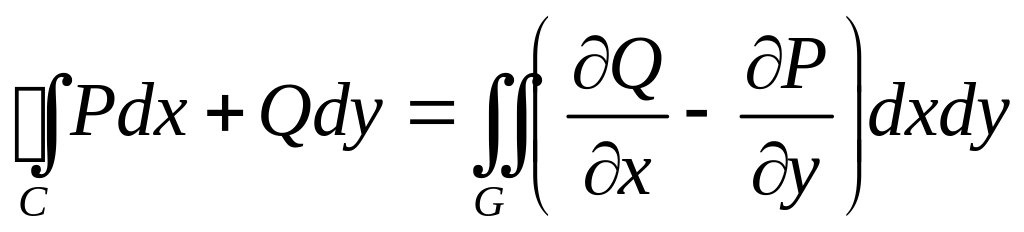(11)
(формула Грина).
Пример 1. . Найти работу силового
поля
при перемещении материальной точки
вдоль первого витка конической винтовой
линии
из точки A(0,0,0) в точку
B(a,0,a).
Решение. Так как
и
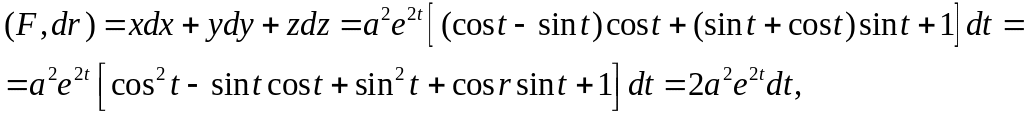то,
учитывая, что t = -
∞ в точке A и t
= 0 в точке B, имеем
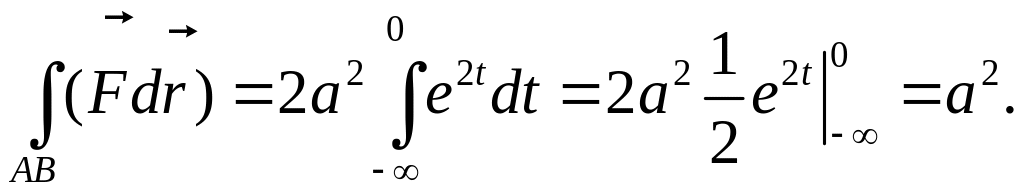
Пример 2. Вычислить криволинейный интеграл
,
где C– окружность
.
Решение. Здесь P(x,y) = x+y, Q(x,y) = - (x-y) и
.
Применяя формулу Грина, получим
=
,
так как
есть площадь круга
.
Задачи для самостоятельного решения:
1. Вычислить работу силового поля
при перемещении материальной точки
вдоль верхней половины эллипса
из точки A(a,0)
в в точку B(-a,0)..
Ответ: πab.
2. Вычислить линейный интеграл
,
если
,
O(0,0), B(1,1)
последующим путям:
а) отрезок прямой OB; б) дуга параболы x2=y;
в) дуга параболы y2=x; г) ломаная OAB, где A(1,0);
д) ломаная OCB, где C(0,1).
Ответ: а)
;
б)0,7; в) 0,7; г) 1; д) 1.
3. Вычислить линейный интеграл
,
если
,
уравнение дуги
:
.
Ответ:
.
4. Вычислить циркуляцию вектора
по окружности
в положительном направлении относительно
орта
.
Решение.
,
или
.
Положим y=tx.
Тогда имеем
,
,
.
Значению t = 0
соответствует точка A(R,0,0),
значениям
- точка B(0,R,0),
значению t= -1 - точка
C(0,0,R). Обходу
в положительном направлении относительно
оси Oz соответствует
обход BCAB, т. е.
изменение t от -∞ через
-1 и 0 до +∞. Далее
,
,
.
Получаем
,
откуда
5. Вычислить циркуляцию вектора
вдоль эллипса
в положительном направлении относительно
орта
.
Ответ: 2πa2.
6. Вычислить работу силового поля
при перемещении материальной точки
вдоль сечения гиперболоида
плоскостью
от токи (a,a,0)
до точки
.
Ответ:
.
7. Используя формулу Грина, вычислить интегралы:
а)
,
где С – контур, образованный
полуокружностью
и осью Ox.
Ответ: 2r2.
б)
,
где С – контур, образованный
синусоидой y = sinx
и отрезком оси Ox при
.
Ответ: - 4π.
в)
Ответ: 0.
г)
,
где С – треугольник с вершинами
O(0,0), A(1,0),
B(0,1).
Ответ:
.
Занятие 4. Поток вектора. Поверхностный интеграл 2-го рода
Пусть G – гладкая поверхность, т.е. поверхность в каждой точке имеет касательную плоскость, положение которой непрерывно изменяется вместе с точкой касания.
В произвольной точке Mo поверхности проведем нормаль, приписав ей одно из двух возможных направлений. Через точку Mo проводим замкнутый контур L проходящий через Mo и не пересекающий границами поверхности.
Если для точки Mo и любого замкнутого контура L, проходящего через нее, после его обхода мы возвращаемся в точку Mo с исходным направлением нормали, то поверхность называется двухсторонней. Выбор определенной стороны поверхности, т. е. выбор направления нормали к поверхности, называется ориентацией поверхности.
Пусть в некоторой части пространства
движется несжимаемая жидкость со
скоростью
зависящей от положения точки M,
и не зависящей от времени t.
Требуется определить объем жидкости
протекающей в единицу времени через
ориентированную двухстороннюю поверхность
G (поток).
Р
азделим
ее произвольным образом на n
частей:
с диаметрами
и площадями
.
Внутри каждой элементарной площадки
возьмем по точке Mk
и вычислим
.
Тогда
Приближенное значение потока через поверхность G получим, суммируя элементарные потоки:
или
Точное значение получим в пределе, когда
:
=
.
если этот предел не зависит ни от способа разбиения поверхности G на частичные поверхности, ни от выбора промежуточных точек Mk. Это – поверхностный интеграл 2-го рода.
Пусть в каждой точке гладкой ориентированной
простой поверхности G
определена векторная функция с
непрерывными проекциями
.
,
а
.
Тогда
=
(12)
или в проекциях на координатные оси
.
(13)
Вычисление поверхностного интеграла 2-го рода сводится к вычислению поверхностного интеграла 1-го рода (12) или к вычислению трех двойных интегралов:
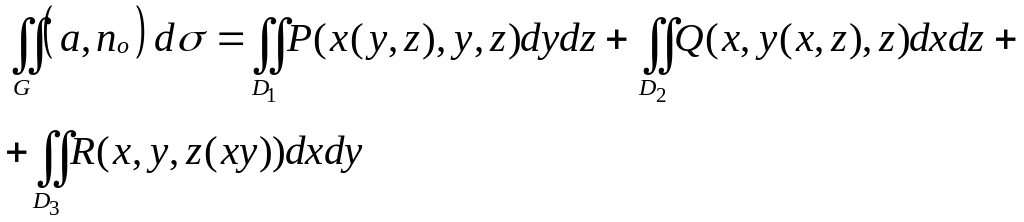(14)
Где D1, D2 D3 - проекции соответственно на плоскости Oyz, Oxz и Oxy, а x(y,z), y(x,z) и z(x,y) выражения, полученные из уравнения поверхности G разрешением относительно соответствующих координат.
Пример 1. Найти поток вектора
через часть поверхности эллипсоида
,
лежащую в первом октанте, в направлении
внешней нормали.
Решение. Вычислим поверхностный интеграл 2-го рода, сведя его к интегралу 1-го рода:
.
Так как в первом октанте внешняя нормаль эллипсоида со всеми осями координат образует острые углы, то все три направляющих косинуса неотрицательны. Поэтому
(Здесь каждый из интегралов по D1, D2, D3 определяет объем одной восьмой части эллипсоида).
Пример 2. Найти поток вектора
через всю поверхность тела
в направлении внешней нормали.
Решение. Переходя к поверхностному
интегралу 1-го рода, имеем:
.
З
аданная
поверхность ограничена сверху сегментом
сферы
,
с боков – частью поверхности гиперболоида
,
снизу кругом На плоскости Oyz
и Oxz поверхность G
проектируется дважды с разных сторон.
Поэтому, в силу симметрии поверхности
относительно этих плоскостей, первые
два интеграла в записи потока равны
нулю:
.
Найдем радиус круга, в который проектируется на плоскость Oxy сферический сегмент.
.
Следовательно,
(область
)
Часть поверхности гиперболоида
проектируется в кольцо
(область
).
Нижним основанием служит лежащий в этой
плоскости круг
(область
).
Но для сегмента сферы cosγ
> 0, для гиперболоида cosγ
< 0, а на нижнем основании z
= 0. Поэтому
.
Для вычисления интегралов перейдем к полярным координа-там:
,
.
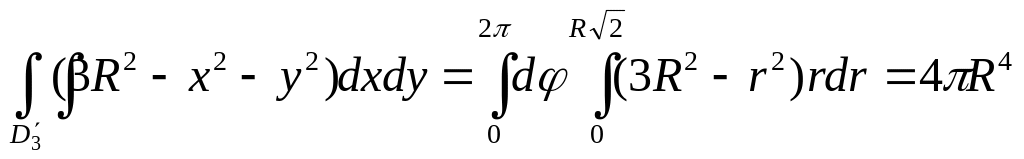Таким образом, окончательно находим:
.
Задачи для самостоятельного решения
1. Найти поток вектора
через всю поверхность тела
в направлении внешней нормали. Ответ:
.
2. Найти поток вектора
через часть поверхности цилиндра
в направлении внешней нормали. Ответ:
3. Найти поток вектора
через часть поверхности параболоида
в направлении внутренней нормали. Ответ:
.
4. Найти поток вектора
через часть поверхности сферы
,
в направлении внешней нормали. Ответ:
.
5. Найти поток вектора
через всю поверхность куба
в направлении внешней нормали. Ответ:
0.
6. Найти поток вектора
через всю поверхность тела
в направлении внешней нормали. Ответ:
.
7. Найти поток вектора
через часть поверхности параболоида
вырезаемую плоскостями x=R,
z=0, x=0,
ориентированной в соответствии с
направлением орта
.
Ответ:
8. Найти поток вектора
через часть поверхности параболоида
,
вырезаемую цилиндром
,
ориентированной в соответствии с
направлением орта
Ответ: 0.
Занятие 5. Теорема Остроградского. Теорема Стокса
Пусть в пространстве Оxyz
дана трёхмерная область Т, ограниченная
гладкой поверхностью σ, ориентированной
по правилу внешней нормали. Пусть функции
Р(x, y,
z), Q(x,
y, z),
R(x, y,
z) непрерывны вместе
со своими частными производными в
замкнутой области
. Тогда имеет место формула Остроградского,
устанавливающая связь интеграла по
поверхности σ с тройным интегралом по
области Т:
(15)
Пусть дано векторное поле
= P(M)
+ Q(M)
+ R(M)
,
причём функции P,Q и R имеют частные производные.
Теперь, используя векторное обозначение поверхностного интеграла и понятие дивергенции (7) формула Остроградского может быть записана в виде
=
(16)
(векторная формула записи).
Поток вектора
через замкнутую поверхность в направлении
внешней нормали равен тройному интегралу
от дивергенции этого вектора, взятому
по области, ограниченной данной
поверхностью.
Пусть дано произвольное векторное поле
,
причём функции Р,Q и R непрерывны вместе со своими производными. Рассмотрим в этом поле двустороннюю кусочно-гладкую поверхность σ, ограниченную кусочно-гладким контуром Г . Пусть прямые параллельные осям координат пересекают поверхность не более чем в одной точке. Выберем ту сторону поверхности, для которой cosγ>0 и ориентируем контур так, чтобы наблюдатель глядя в конец вектора π0, видел обход контура Г против часовой стрелки. Тогда имеет место формула Стокса:
+
+
(17)
Переходя в левой части равенства к векторным обозначениям и пользуясь в правой части понятием ротора (8), получим векторную форму записи формулы Стокса:
(18)
Пример 1. Используя теорему
Остроградского, найти поток вектора
через всю поверхность тела
в направлении внешней нормали.
Решение. Имеем
.
Поэтому по формуле (15)
.
Для вычисления тройного интеграла
перейдем к цилиндрическим координатам:
Уравнение поверхности принимает вид
.
.
Пример 2. Проверить ответ примера 2 в занятии 4 при помощи теоремы Стокса.
Решение. Так как
,
то P=z,
Q=x,
R=y
и по формуле (9)
.
За поверхность G
,ограниченную контуром L
примем сам круг, образованный сечением
шара
плоскостью
.
Центр круга
;
его радиус
.
Единичный вектор нормали
.
Так как
,
то по формуле (18) находим
.
Пример 3. Найти циркуляцию вектора
вдоль эллипса, образованного сечением
гиперболоида
плоскостью
в положительном направлении орта
Ответ проверить при помощи теоремы
Стокса.
Решение. Параметрические уравнения заданного эллипса
x=Rcost, y=Rcost, z=Rsint. Для обхода эллипса в заданном направлении параметр t надо изменять от 0 до2π. Следовательно,
.
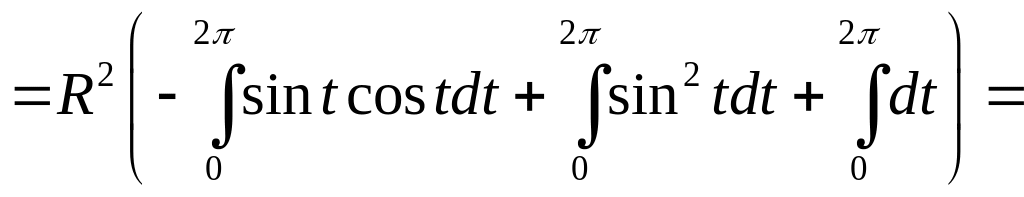
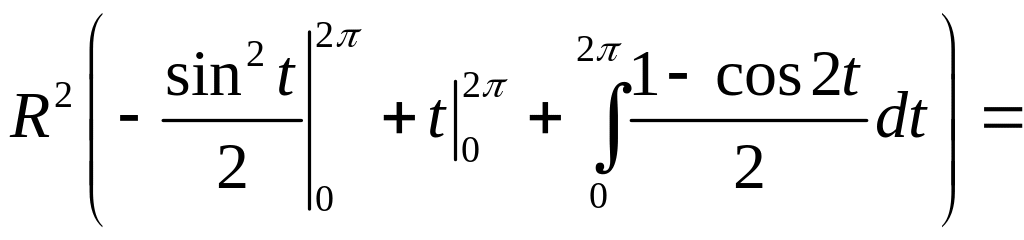
Применим теорему Стокса. Имеем
.
За поверхность G,
ограниченную контуром L,
часть секущей плоскости, лежащей внутри
эллипса. Единичный вектор нормали,
направленный в нужную сторону имеет
вид
.
Поэтому
и
,
но так как эллипс имеет полуоси
и
,
то
.
Задачи для самостоятельного решения
I. Используя теорему Остроградского, решить следующие задачи:
1. Доказать, что поток радиус-вектора
через любую кусочно гладкую замкнутую
поверхность в направлении внешней
нормали равен утроенному объему тела,
ограниченного этой поверхностью.
2. Найти поток вектора
через всю поверхность куба
в направлении внешней нормали. Ответ:
a5.
3. Найти поток вектора
через всю поверхность сферы
в направлении внешней нормали. Ответ:
4πR2.
4*. Найти поток вектора
,
направленный в отрицательную сторону
оси Ox через поверхность
части параболоида
,
отсекаемой плоскостью x=R.
Ответ: - πR3.
Указание: замкнуть поверхность, добавив основание параболического сегмента, и вычесть соответствующую часть потока.
5. Найти поток вектора
через всю поверхность тела
,
в направлении внешней нормали. Ответ:
.
6. Найти поток вектора
через всю поверхность тела
,
в направлении внешней нормали. Ответ:
.
II. Задачи к теореме Стокса:
1. Жидкая среда вращается с угловой
скоростью
вокруг оси, проходящей через начало
координат. Найти ротор поля скоростей
этой седы. Ответ:
.
Указание: скорость
точки
,
вращающейся с угловой скоростью
вокруг оси, проходящей через начало
координат, равна
.
2. При помощи теоремы Стокса вычислить
циркуляцию вектора
по сечению сферы
плоскостью
в положительном направлении относительно
орта
.
Ответ:
.
3. Вычислить циркуляцию вектора
по сечению гиперболоида
плоскостью
в положительном направлении относительно
орта
.
Проверить при помощи теоремы Стокса.
Ответ:
.
4. Вычислить циркуляцию вектора
по контуру, вырезаемому в первом октанте
из параболоида
плоскостями x=0, y=0,
z=R в
положительном направлении относительно
внешней нормали параболоида. Проверить
при помощи теоремы Стокса. Ответ:
.
Занятие 6. Оператор Гамильтона. Дифференциальные операции 2-го порядка
Все операции векторного анализа можно
выразить при помощи оператора Гамильтона
– символического оператора
(читается - набла), определяемого
равенством
Применяя формально известные операции умножения вектора на скаляр, скалярного и векторного произведения двух векторов, находим
=
=
;
;
=
;
=
/
По аналогии с производной по направлению
от скалярной функции
вводится понятие производной по
направлению единичного вектора
от векторной функции
.
Именно,
=
.
Производные по направлению произвольного
(не единичного ) вектора
отличаются только тем, что в них входит
дополнительный скалярный множитель
:
.
Применяя оператор , следует лишь помнить, что это дифференциальный оператор и не забывать правило дифференцирования произведения.
Пример 1. Найти градиент произведения двух скалярных функций u и v.
Решение. Имеем:
(штрих указывает функцию, на которую
действует оператор). Но
и
.
Таким образом,
Пример 2. Найти
,
где
- постоянный вектор.
Решение. По формуле векторной алгебры
.
Поэтому, учитывая соотношение
,
имеем:
.
Но
,
а это есть производная вектора
по направлению вектора
.
Далее
.
Таким образом,
.
Если принять величины
,
за исходные, то выполнив над ними
дифференциальные операции первого
порядка, получим дифференциальные
операции второго порядка над функциями
u(М) и
(М).
Их пять:
1) divgradu=
=
=
=
,
где
Δ=
-
оператор Лапласа;
2) rotgradu=
=
;
3)
=
;
4) divrot
=
5)
=
.
Вторая и четвертая операции приводят к нулю:
rotgradu=
=0,
divrot
=
.
Это следует из векторного смысла оператора : в первом случае формально мы имеем векторное произведение двух коллинеарных векторов, а во втором – смешанное произведение трех компланарных векторов.
Задачи для самостоятельного решения
Выполнить следующие дифференциальные операции (здесь и далее c – постоянный, a и b – переменные векторы):
1. Найти div(cu) div(au)
Ответ: div(cu)=(c, gradu); div(a, u)=udiva+(a, gradu).
2**. Найти grad(a, c) grad(a, b)/
Ответ:
,
.
Решение. Предварительно найдем
.
Имеем:
.
Отсюда
;
далее,
и используем предыдущий результат.
3. Найти div[a,c] и div[a,b].
Ответ: div[a,c]=(c,rota), div(a,b)=(b,rota)-(a,rotb).
4. Найти rot(cu), rot(au) rot[a,b].
Ответ:
.
Указание: смотри решение примера 2.
5. Получить выражения для
,
,
,
через производные скалярного или
векторного полей.
Ответ:
,
,
.
6. Найти
,
если
Ответ:
.
7. Найти
,
если
.
Ответ: 0.
8. Найти
,
если
Ответ:
9. Найти
.
Ответ:
.
10. Найти
и
.
Ответ:
,
7.
.
11. Найти
.
Ответ:
Занятие 7. Специальные виды векторных полей
Векторное поле
называется потенциальным, если вектор
поля
является градиентом некоторой скалярной
функции u=u(P)
(работа в этом поле не зависит от формы
пути):
=
.
Функцию u(P)
в этом случае называют потенциалом
векторного поля. Необходимым и достаточным
условием потенциальности дважды
дифференцируемого в односвязной области
поля
является равенство нулю ротора этого
поля:
.
Потенциальное поле обладает следующими
свойствами.
1. В области непрерывности потенциала линейный интеграл от вектора поля, взятый между двумя точками, не зависит от формы пути интегрирования и равен разности значений потенциала поля в конце и начале пути интегрирования
=
=
=u(B)
– u(A)
(19)
(т.к.
,
что легко проверяется).
2. Циркуляция вектора по любому замкнутому контуру, лежащему в области непрерывности поля, равна нулю.
3. Потенциал поля u(P) в произвольной точке P может быть вычислен по формуле(19):
(20)
Причем C = u(A).
Для вычисления интеграла (20) можно применять любой путь – проще всего в качестве такого пути выбрать ломаную со звеньями, параллельными осям координат, соединяющую точки A и P.
Пример 1. Проверить, что ротор
трехмерного векторного поля
тождественно равен нулю (функция u(P)
предполагается дважды дифференцируемой).
Решение. Так как
,
то учитывая равенство смешанных
производных 2-го порядка, получаем
.
Этот результат сразу получается с помощью оператора Гамильтона.
Пример 2. Найти потенциал поля
.
Решение. Убедимся, что поле потенциально:
.
Следовательно,
.За
путь интегрирования примем ломаную
OABP, где O(0,0,0),
A(X,0,0),
B(X,Y,0),
P(X,Y,Z).
Находим:
=
=
=
=
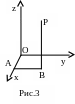+С,
.Так
как на OA имеем
,
то
.
Аналогично на AB имеем
,
,
,
поэтому
.
На BP имеем
,
,
значит,
.
Таким образом,
.
Возвращаясь к переменным x,
y, z,
получаем
.
Замечание. Рассмотренный метод нахождения потенциала поля применяется при решении таких задач математического анализа, эквивалентных решенной, как восстановление функции двух, трех и n переменных по их полным дифференциалам, а так же при интегрировании дифференциальных уравнений в полных дифференциалах.
Векторное поле
называется соленоидальным, если
.
Для трехмерного случая. Это условие
имеет вид
.
(21)
Векторное поле называется гармоническим (или лапласовым), если оно одновременно и потенциальное и соленоидальное, т.е. если и .
Пример 3. Доказать, что для любого
дважды дифференцируемого трехмерного
векторного поля
поле ротора соленоидально.
Решение. Имеем
.
Учитывая равенство смешанных производных 2-го порядка, получаем
.
Этот результат сразу получается с
помощью оператора Гамильтона.
Пример 4. Доказать, что потенциал u
двумерного или трехмерного лапласова
поля является гармонической функцией
двух или трех переменных (т. е.
или
).
Решение. Действительно, имеем
для двух переменных и
для трех переменных.
Пример 5. Показать, что потенциал
поля сил тяготения, возникающего в
пространстве, окружающем некоторую
точечную массу, равен
(k – константа) и что
поле сил тяготения лапласово.
Решение. Поместим начало координат в центре притяжения. Тогда
.
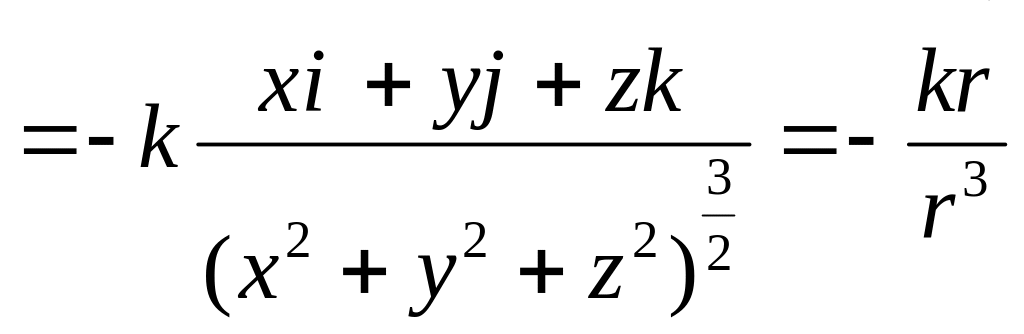Но это – вектор силы притяжения.
Действительно, он направлен к центру
притяжения, поскольку
- единичный вектор радиус-вектора точки
,
направленный к началу координат, а его
модуль равен
,
т. е. обратно пропорционален квадрату
расстояния от центра притяжения. Покажем,
что
.
Имеем
.
.
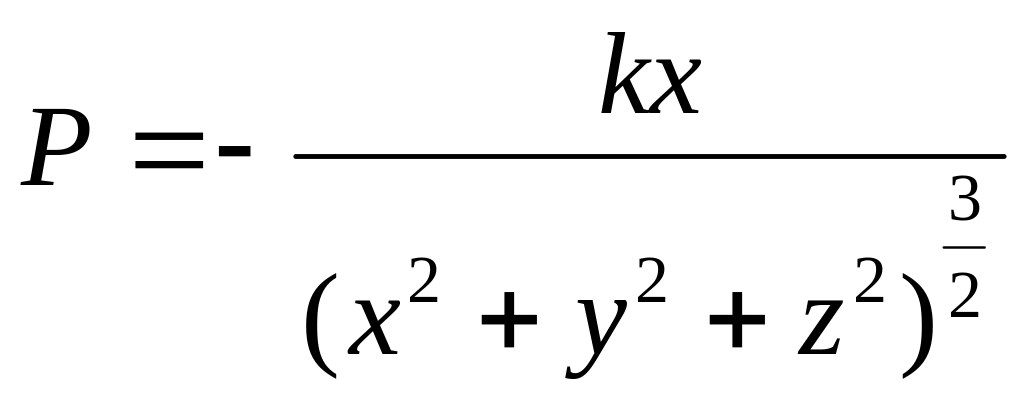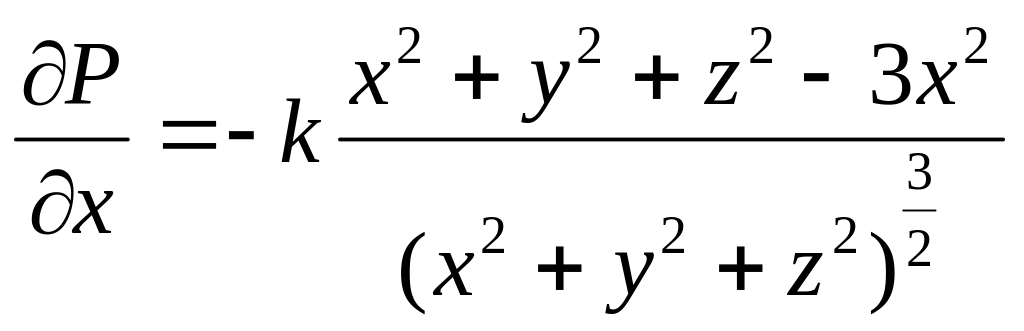
Аналогично
,
,
и потому
.
Таким образом, поле сил тяготения лапласово.
Задачи для самостоятельного решения
Доказать, что в соленоидальном поле поток вектора через замкнутую поверхность, не содержащую внутри особых точек, равен нулю.
Проверить соленоидальность следующих полей:
1.
.
2.
.
3.
.
4.
.
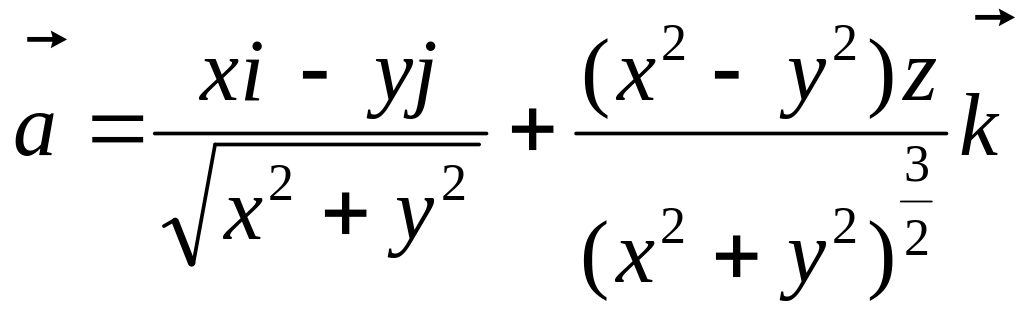5. Доказать, что плоское векторное поле,
потенциалом которого служит функция
,
лапласово.
6. Являются ли гармоническими следующие функции:
а)
;
Ответ: нет.
б)
;
Ответ: нет.
в)
.
Ответ: да.
г)
;
Ответ: только при
д)
.
Ответ: только при
.
е)
.
Ответ: да.
Расчетные задания
Задача 1. Найти производную скалярного поля u(x,y,z) в точке M по направлению нормали к поверхности S, образующей острый угол с положительным направлением оси Oz.
1.1.
1.2
1.3.
1.4
1.5
1.6.
1.7.
1.8.
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
Найти производную скалярного поля
u(x,y,z)
в точке M по направлению
вектора
.
1.1
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1. 24.
1.25.
1.26.
1.27.
1.28.
1.29.
1.30.
Задача 2. Найти угол между градиентами скалярных полей u(x,y,z) и v(x,y,z) в точке M.
2.1.
.
2.2.
.
2.3.
.
2.4.
.
2.5.
.
2.6.
.
2.7.
.
2.8.
.
2.9.
.
2.10.
.
2.11.
.
2.12.
.
2.13.
,
.
2.14.
.
2.15.
,
.
2.16.
.
2.17.
.
2.18.
.
2.19.
.
2.20.
.
2.21.
.
2.22.
.
2.23.
,
.
2.24.
.
2.25.
.
2.26.
.
2.27.
.
2.28.
,
.
2.29.
.
2.30.
.
Задача 3. Найти поток векторного поля через часть поверхности S вырезаемую плоскостями P1, P2 (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
3.1.
,
,
.
3.2.
,
.
3.3.
,
.
3.4.
,
.
3.5.
,
,
.
3.6.
,
.
3.7.
,
,
.
3.8.
,
,
.
3.9.
,
,
.
3.10.
,
,
.
Найти поток векторного поля через часть поверхности S вырезаемую плоскостью P (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
3.11.
,
,
.
3.12.
,
.
3.13.
,
.
3.14.
.
3.15.
,
.
3.16.
,
.
3.17.
,
.
3.18.
,
.
3.19.
,
.
3.20.
,
.
3.21.
,
.
3.22.
,
.
3.23.
,
.
3.24.
,
.
3.25.
,
.
3.26.
,
.
3.27.
,
.
3.28.
,
.
3.29.
,
.
3.30.
.
Задача 4. Найти поток векторного поля через часть плоскости P, расположенную в I октанте(нормаль образует острый угол с осью Oz).
4.1.
,
.
4.2.
,
,
4.3.
,
.
4.4.
,
.
4.5.
,
,
4.6.
,
.
4.7.
,
.
4.8.
,
.
4.9.
,
.
4.10.
,
.
4.11.
,
.
4.12.
,
.
4.13.
,
.
4.14.
,
.
4.15.
,
.
4.16.
,
.
4.17.
,
.
4.18.
,
.
4.19.
,
.
4.20.
,
.
4.21.
,
.
4.22.
,
.
4.23.
,
.
4.24.
,
.
4. 25.
,
.
4.26.
,
.
4.27.
,
.
4.28.
,
.
4.29.
,
.
4.30.
,
.
Задача 5. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).
5.1.
(первый
октант).
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
(I
октант)
5.12.
5.13.
5.14.
(I октант)
5.15.
5.16.
5.17.
5.18.
5.19.
(I
октант)
5.20.
5.21.
5.22.
5.23.
5.24.
5.25.
5.26.
(первый
октант)
5.27.
5.28.
5.29.
5.30
.
Задача 6. Найти модуль циркуляции векторного поля вдоль конура Г.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19.
6.20.
6.21.
6.22.
6.23.
6.24.
6.25.
6.26.
6.27.
6.28.
6.29.
6.30.
