3.2. Характеристика систем управления технологическими процессами

Взаимосвязанную совокупность оборудования, на котором вы­полняется технологический процесс, назовем технологической си­стемой. Отвлекаясь от физической сущности, представим техноло­гическую систему в виде многомерного объекта, описываемого тремя группами переменных.

Первую группу переменных обозначим вектором W (t}, составляющие которого W₁ (t), ..., W_m (t) представляют собой параметры, характеризующие свойства и количество входных про­дуктов (температура, химический состав, механические свойства, размеры, количество и т. п.). Вторая группа переменных V (t) = {V₁ (t), ..., V_n(t)} представляет собой параметры, характе­ризующие свойства выходного продукта. Третья группа составлена из параметров, характеризующих условия протекания технологического процесса. Обозначим их векторной переменной Z (t} = {Z₁ (t), ...,Z.i (t).} К этим параметрам, как правило, относятся давление и температура в технологическом агрегате, скорость и координаты рабочих частей механизма, производительность и др. Выделим среди перечисленных переменных те, которые могут ха­рактеризовать состояние технологической системы (вектор состоя­ния), и управляющие переменные (вектор управления).

В общем случае состояние технологической системы характери­зуется всеми выделенными выше переменными. Действительно, для определения управляющего воздействия нужна информация как о свойствах и количестве входных и выходных продуктов, так и об условиях протекания процесса. Однако размерность векторов W (t), V (t) и Z (t) в реальных технологических системах обычно весьма велика и превышает возможности управляющего органа (оператора или автоматического устройства) по обработке инфор­мации. Кроме того, на практике часть переменных либо не требуется измерять, т. е. они несущественны с точки зрения цели управления, либо измерять невозможно из-за технических сложностей.

Поэтому только часть составляющих векторов W (t), V (t) и Z (t) используют для формирования вектора состояния х (t}. Пере­менные вектора состояния условно разобьем на две группы. В пер­вую группу включим те переменные, которые можно целенаправ­ленно изменять в процессе управления. Назовем их управляемыми переменными. Вторую группу составим из переменных, которые из­меряются и используются при формировании управляющего воз­действия, но не могут целенаправленно изменяться при управлении данным технологическим процессом. Таки­ми переменными являются, например, по­казатели качества входного продукта. Их необходимо учитывать при управлении, но активно влиять на них невозможно.

В качестве управляющих переменных обычно выбирают те составляющие векто­ров W (t) и Z (t), целенаправленное из­менение которых технически возможно и существенно влияет на показатель цели управления.

Таким образом, выбор переменных для описания состояния и управляющих переменных зависит от цели управления техноло­гическим процессом, от возможностей измерения свойств входных и выходных продуктов, а также от особенностей и физических свойств технологической системы.

Переменные векторных функций W (t) и Z (t}, не использован­ные при формировании вектора состояния и вектора управления, могут рассматриваться как неконтролируемые возмущающие воз­действия, приложенные к технологической системе (вектор возму­щений).

Рис.15 Схема технологической системы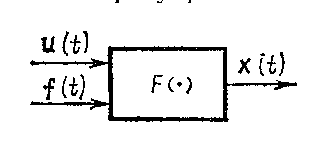

Поэтому технологическую систему можно представить схемой (рис.15). На ее информационные входы действуют векторные функ­ции u(t) (вектор управления) и f (t} (вектор возмущения), а на информационном выходе — векторная функция х (t) (вектор со­стояния), т. е. технологическую систему можно представить как преобразователь функций u (t) и f (t) в функцию х (t). Каждая вы­ходная переменная х₁ (t), ..., X_k (t) в общем случае определяется всеми входными переменными. Поэтому /5/

x(t) = F(u(t), f(t)) (7)

где F—оператор преобразования.

Выражение (7) является формальным описанием технологиче­ской системы, т. е. моделью. Конкретное выражение оператора F зависит от физических свойств технологической системы и уста­навливается при ее идентификации .

Определим технологический процесс как целенаправленную смену состояний технологической системы во времени. Формально его можно описать вектор-функцией х (/) = {x₁(t), ..., x_k(t)}. Таким образом, состояние технологического процесса и состояние технологической системы характеризуются одними и теми же пере­менными x₁, x₂, ... , x_k которые назовем параметрами технологиче­ского процесса.

Задачу управления технологическим процессом можно сформу­лировать следующим образом: найти такое состояние технологиче­ского процесса х* (t) (технологический режим) и такое управляющее воздействие u* (t), которые удовлетворяют как цели управления, так и ограничениям вида (3). В большинстве практических случаев при управлении технологическим процессом определение программы управления (плана) х* (t) и формулирование управляющего воздей­ствия u* (t} (регулирование) разделены по времени и осуществляются в форме двух последовательных процедур.

Графически управление технологиче­ским процессом можно представить в про­странстве параметров его состояния х (t) следующим образом (рис. 16). Программа управления — это фазовая траектория х* (t}. Ход технологического процесса представляется фазовой траекторией Х_p (t), которая описывает процесс регулирования.

Траектории х* (t) и Кр (t) совпадают лишь в идеальном случае. Реальный процесс несколько отклоняется от х* (t).

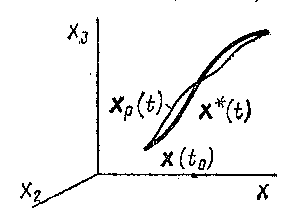
Рис.16 Графическое представление процесса управления технологией

В промышленности существует множество типов технологиче­ских процессов, отличающихся физическими законами, положен­ными в их основу, оборудованием, на котором они выполняются, условиями их протекания, качеством исходного сырья и др. Однако, несмотря на большое разнообразие технологических процессов, системы управления ими могут быть разделены на типы по сходству целей и алгоритмов управления. Рассмотрим основные типы систем управления технологическими процессами.

Системы программного регулирования. Если технологический режим не зависит от внешних условий (например, качества исход­ного сырья) и может быть рассчитан заранее, то целью управления является минимизация отклонения текущих значений управляемых переменных от заданных, т. е. требуется осуществлять регулиро­вание технологического процесса по заданной программе. Фор­мально программу регулирования можно выразить вектором х* (t). Тогда процесс программного регулирования в пространстве техно­логических параметров можно представить как движение по фазовой траектории х (t), близкой к х* (t) (рис. 16). Введя меру близости этих траекторий, можно определить качество регулирования тех­нологического процесса.

В частном случае, когда все составляющие вектор-функции х* (t) — постоянные величины, т. е. x*₁ = const, x*₂ == const, ... x*_k = const, процесс регулирования сводится к стабилизации технологических параметров. Системы, осуществляющие такое ре­гулирование, называют системами стабилизации.

Примерами процессов, требующих программного регулирова­ния параметров, могут служить: термическая обработка материа­лов, в ходе которой температура в печи изменяется по заранее определенному закону; резание металлов, при котором координаты рабочих органов изменяются по заданной программе. Системы стабилизации используются для поддержания постоянных значе­ний напряжения электрогенераторов, числа оборотов электродви­гателя, давления, температуры, расхода компонентов сырья, кон­центрации в химико-технологических процессах.

Регулирование параметров характерно для непрерывных тех­нологических процессов. В дискретных процессах технологический режим часто определяется порядком и длительностью выполнения технологических операций. Переход к очередной операции осуще­ствляется после окончания предыдущей и может быть как условным” так и безусловным. В технологических процессах такого типа программное регулирование заключается в реализации последова­тельности и длительности операций в соответствии с заданной про­граммой.

Системы оптимизации параметров технологических процессов. В ряде процессов наилучший в определенном смысле технологиче­ский режим не может быть задан заранее, так как его выбор зави­сит от ряда факторов, информация о которых появляется в ходе процесса. Рассмотрим, например, процесс, в котором для опреде­ления технологического режима, обеспечивающего наилучшее ка­чество выходного продукта, необходимо знать свойства входного продукта. Если свойства этого продукта изменяются в широких пределах и закон изменения неизвестен, то рассчитать технологиче­ский режим заранее невозможно. Следовательно, его требуется оп­ределять при управлении технологическим процессом. Предполо­жим, что зависимость качества выходного продукта от свойств входного описывается функцией Q = Q [х_k(t), х (t)], где х (t) — текущее значение управляемых переменных; Х_k (t) — контролируе­мые переменные, характеризующие свойства входного продукта.

Для определения технологического режима требуется найти такое значение х (t) = х* (t), которое обеспечивает /6/

maxQ=Q( x_k(t), x*(t)). (8)

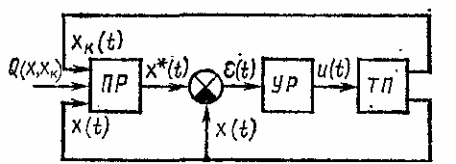
Рис.17 Схема системы экстремального управления

Технологический режим х* (t) является оптимальным по кри­терию (8). Возможная схема системы, реализующей описанное управление для технологического процесса с одной управляемой переменной, изображена на рис. 17. Вычислительное устройство, которое назовем программатором ПР, получает информацию о те­кущих значениях управляемой переменной х (t) и переменной х_k. (t), характеризующей свойства входного продукта, и на основе крите­рия оптимальности (8) вычисляет х* (t). По ошибке регулирова­ния  (t), определяемой элементом сравнения, устройство регулиро­вания УР формирует регулирующее воздействие и (t).

Кроме критерия оптимальности, описанного в примере, воз­можны и другие. В частности, весьма распространены критерии, на основе которых выбирается наилучший в экономическом смысле технологический режим при заданном уровне качества выходного продукта. При этом используются такие экономические показатели, как стоимость потребляемой энергии, компонентов входных продук­тов, себестоимость выходного продукта и др.

Таким образом, для осу­ществления оптимального уп­равления необходимо, во-пер­вых, экстремизируя заданный критерий, найти оптимальную программу управления (тех­нологический режим), во-вто­рых, регулировать технологический процесс, используя техно­логический режим как задающее воздействие. Построенные на этом принципе системы управления являются оптимальными по про­грамме управления и называются экстремальными системами уп­равления.

Кроме программы управления объектом оптимизации могут быть динамические характеристики технологического процесса. Рас­смотрим простой пример. Пусть технологи­ческий режим задан в виде вектор-функции х* (t). Для простоты будем считать, что х* = const. В пространстве технологических параметров х* можно представить точкой (рис. 18).

Рис.18 К оптимизации динамических характеристик технологического процесса

Текущее состояние технологиче­ского процесса в момент времени t₀ обозна­чим Хо. Если x₀  х*, то управление иллюст­ративно можно представить как переход из точки х₀ в х*. Очевидно существует множе­ство траекторий, связывающих эти точки. Задача оптимизации заключается в выборе траектории, наилучшей в смысле определен­ного критерия. Необходимость такой оптимизации возникает в тех случаях, когда уровень качества выходного продукта или экономическая эффективность существенно зависит от переходного процесса.

Системы оптимизации порядка выполнения технологических операций. Выше отмечалось, что в дискретных процессах техноло­гический режим определяется порядком и длительностью выполне­ния технологических операций. Выбор порядка и длительности, т. е. программы управления, заключается в определении времени начала и окончания операций на определенном станке с учетом заданной технологии обработки деталей, производительности стан­ков, длительности их переналадки и ряда других факторов. Крите­рием оптимальности является время технологического цикла, ко­торое требуется минимизировать.

Для оптимального выбора программы требуется решить задачу комбинаторного типа, размерность которой зависит от разнообра­зия обрабатываемых деталей и числа обрабатывающих станков. Число различных вариантов программы оценивается величиной (m!)ⁿ, где m — число типов обрабатываемых деталей, п — число обрабатывающих станков. Очевидно, даже для небольшого техно­логического участка (три-четыре станка, пять-шесть деталей) число вариантов программы оказывается столь большим, что исключает возможность использования простых вычислительных алгоритмов для отыскания оптимального решения. Практическая значимость задач этого типа обусловила развитие большого количества методов их решения, совокупность которых составляет теорию расписания или календарное планирование.

Дискретное производство в отличие от непрерывного характе­ризуется большей стабильностью технологического режима, что позволяет рассчитывать его заранее, а в процессе управ­ления осуществлять лишь оперативное регулирование. Поэтому выбор программы управления в дискретных производственных процессах

выделен в самостоятельную функцию управления — планирование работы технологических подразделений (участок, линия и т. п.).

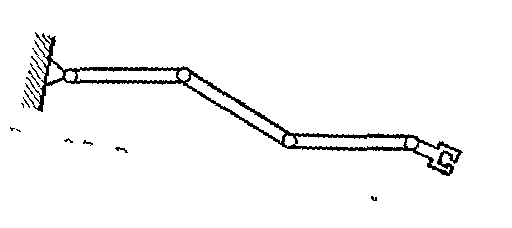
Системы управления манипулированием. Операции манипули­рования выполняются устройствами, в некоторой степени имити­рующими двигательные функции человека. Эти устройства принято называть роботами-манипуляторами.

Рис.19 Вариант кинематической схемы манипулятора

На рис. 19. показан вариант кинематической схемы манипу­лятора, представляющей собой три шарнирно соединенных звена и схвата — устройства, с помощью которого можно держать деталь или инструмент. Изменяя координаты х_i, y_i, z_i, (i =0, 1, 2, 3) шар­ниров, можно изменять положение схвата. Одной из главных задач управления манипулированием является определение таких траек­торий движения звеньев манипулятора (в данном случае шарни­ров) в заданной системе координат.