ГОУВПО

“Воронежский государственный технический университет “

Кафедра робототехнических систем

Методические указания к выполнению

контрольной работы № 1 и лабораторных работ № 1 – 3 по дисциплине ”Теория автоматического управления”

для студентов специальности

”Технология машиностроения”

заочной формы обучения

Воронеж 2008

Составители: канд. техн. наук А.П. Харченко,

канд. техн. наук В.В. Кольцова

УДК 612.313

Методические указания к выполнению контрольной работы №1 и лабораторных работ №1-3 по дисциплине “Теория автоматического управления” для студентов специальности 151001 “Технология машиностроения”, заочной формы обучения / Воронеж. гос. техн. ун-т: Сост. А.П. Харченко, В.В. Кольцова. Воронеж, 2009. 35 с.

В методических указаниях представлена контрольная работа по расчету математических моделей и переходных характеристик элементов систем регулирования, как типовых динамических звеньев.

Предложены схемы моделирования двигателя и систем автоматического регулирования скорости с использованием системы инженерных расчетов Matlab.

Методические указания подготовлены на магнитном носителе в текстовом редакторе MS Word 7.0 и содержатся в файле метТМgo. doc

Ил. 20. Табл. 3. Библиогр.: 3 назв.

Рецензент канд. техн. наук, доц. В.А. Трубецкой

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.И. Шиянов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ГОУВПО «Воронежский государственный

технический университет», 2008

Введение

Производительность и качество технологического процесса в машиностроении определяются основным (станки-автоматы) и вспомогательным ( системы загрузки-выгрузки ) технологическим оборудованием.

Производительность основного технологического оборудования (металлообрабатывающих станков и различного вида прессов) зависит от следующих параметров:

скорости обработки деталей;

времени разгона и торможения исполнительного органа;

времени перехода с одной скорости на другую (скорости вращения шпинделя);

скорости перемещения резца;

скорости перемещения координатного стола;

скорости перемещения исполнительного органа пресса.

Скорость обработки деталей определяется технологическим процессом и параметрами используемого для данных движений исполнительного двигателя.

Время разгона и торможения двигателя можно изменять путем применения систем регулирования.

Качество систем регулирования определяет:

точность обработки детали;

плавность перемещения исполнительного органа, связанного с помощью кинематической схемы (редуктора в теории управления) с исполнительным двигателем.

Основные технические характеристики систем регулирования отражены в следующих технических показателях:

точность обработки деталей;

максимальная и минимальная скорости;

плавность разгона и торможения.

Точность обработки деталей определяется допустимой ошибкой в системе регулирования.

Максимальная скорость определяется возможностями исполнительного двигателя и способом регулирования его скорости.

Минимальная скорость определяется ошибкой в системе регулирования и точностью датчика скорости или датчика перемещения (измерителя скорости вращения и перемещения вала двигателя).

В качестве исполнительных двигателей в системах регулирования используются электрические двигатели постоянного и переменного тока.

Наиболее распространено использование двигателя постоянного тока, управляемого по якорной цепи (обмотка, расположенная на вращающейся части двигателя – роторе).

В теории управления для оценки процессов разгона и торможения, различных законов изменения скорости вращения во времени используется математическое моделирование, то есть замена элемента или системы моделью.

Математическая модель представляет собой систему уравнений, описывающую физические процессы в элементе или в системе в целом.

В этих уравнениях переменными являются входной сигнал (вход элемента или системы) и выходной сигнал (выход элемента или системы).

Константы в уравнениях определяются техническими характеристиками элементов, при этом влияние параметров окружающей среды и условий работы станка (твердость заготовок деталей) можно учитывать путем усложнения математической модели.

Используя при моделировании различные законы изменения входного сигнала, можно оценить закон изменения и форму выходного сигнала системы

Лекция № 1

1. Основные понятия и определения в теории управления

2. Типовые входные сигналы в технических системах

3. Система УЧПУ-МРС

1. Теория автоматического управления (ТАУ) – это техническая дисциплина, основанная на использовании математического представления систем и их элементов.

При проектировании современных технических систем используется методы анализа и синтеза технических систем путем компьютерного моделирования.

Компьютерное моделирование использует различного вида программы, где математическое представление систем и их элементов положено в основу схем моделирования.

Объектом управления в машиностроении является различного вида металлорежущие станки (МРС), расположенные в цехе механообработки.

Управление работой цеха определяется и управлением работой МРС.

Управление – это такая организация работы МРС в ходе технологического процесса по обработке деталей различных конфигураций, которая обеспечивает достижение поставленных целей.

Целью управления МРС в цехе механообработки является обеспечение заданной производительности и качества.

Производительность обеспечивается временем выполнения основной и вспомогательной технологической операции.

Качество определяется точностью, то есть соответствием заданных параметров и выполненных в процессе управления.

Время выполнения операции называется быстродействием системы.

Точность в ТАУ оценивается величиной обратной называемой ошибкой.

Обеспечение заданных высокого быстродействия и допустимой ошибки являются основными задачами при проектировании технических систем.

В ходе выполнения основных задач управления решаются следующие вопросы:

определение функциональной схемы системы;

определение уравнения системы и основных элементов системы;

определение структурной схемы системы на основе математических моделей элементов;

определение влияния параметров элементов на свойства системы;

выбор дополнительных элементов в системы в соответствии с заданными техническими параметрами;

определение параметров выбранных дополнительных элементов системы.

Функциональная схема системы определяется назначением системы для управления МРС. Система управляет или скоростью перемещения исполнительного органа МРС или величиной перемещения.

Уравнения элементов основаны на описании принципа его работы.

Структурная схема используется как схема моделирования реальной технической системы.

Влияние параметров элементов оценивается по виду переходных процессов в системе.

В ТАУ для получения параметров системы специально вводятся дополнительные элементы – регуляторы.

В технической системе это регуляторы скорости, регуляторы перемещения и т.д. Параметры и типы регуляторов при моделировании изменяются.

Определение параметров регуляторов базируется на переводе математического представления в техническую реализацию элемента

2. Работа группы станков в механическом цехе характеризуется следующими режимами работы:

ручном;

полуавтоматическом;

автоматическом.

Ручной режим характеризуется управлением работы станка человеком. Производительность обеспечивается квалификацией человека и техническими параметрами станка.

Полуавтоматический режим работы характеризуется совместной работой человека и механизмов на определенных этапах обработки деталей в станке.

Автоматический режим работы характеризуется непрерывной работой станка по заданной программе в течении технологического процесса. Человек–оператор вмешивается на этапах настройки программы и отладки процесса обработки деталей на определенном типе станка.

Рассмотрим МРС, упрощенная схема которого представлена на рис. 1. В МРС выделим кинематическую схему КС и исполнительный орган ИО. На входе и выходе КС имеем значения угловых скоростей Ω1 и Ω2, на КС действует некоторый момент сопротивления Мс.

Ω1 Мс Ω2

Рис. 1. Упрощенная схема МРС

При работе станка в автоматическом режиме используются следующие входные сигналы (команды):

включение – вкл;

выключение – выкл;

включение-выключение – вкл/выкл;

переключение с одной скорости на другую – перекл.

На рис. 2 представлены временные диаграммы входных сигналов МРС. Входные сигналы, как видно из временных диаграмм, прямоугольной формы.

Рис. 2. Временные диаграммы входных сигналов МРС

Для достижения высокой производительности при работе станка с такими входными сигналами необходимо обеспечить точность отработки формы сигнала и быстродействие, то есть максимальное соответствие изменений входа и выхода. МРС обладает инерционностью вследствие наличия момента инерции КС. С другой стороны для КС необходимо ограничивать ускорения и скорости входных сигналов.

3. Работой МРС в автоматическом режиме управляет устройство числового программного управления (УЧПУ).

На рис.3 представлена схема системы УЧПУ – МРС с указанием входных Х и выходных Y сигналов МРС.

Х Y ИО

ОС

Рис. 3. Схема системы УЧПУ – МРС

Выходной сигнал У – это сигнал управления ИО, которым является резец или шпиндель станка. Сигнал обратной связи (ОС) – это информация от датчиков о параметрах ИО.

Система УЧПУ – МРС является системой с ОС. МРС включает в себя КС, исполнительные двигатели Д, датчики обратной связи ДОС и электрооборудование. МРС – это инерционная система.

УЧПУ является системой управления (СУ), формирующей закон изменения входных сигналов Х.

При моделировании систем и их элементов используется графическое изображение в виде квадрата, представленного на рис. 4, где МО – это математическое описание.

Х У

Рис. 4. Графическое изображение

Рассмотрим функциональную схему системы УЧПУ – МРС, представленную на рис. 5.

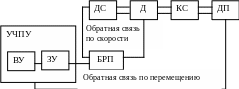
Рис. 5. Функциональная схема системы УЧПУ – МРС:

УЧПУ – система управления;

ВУ – вычислительное устройство;

ЗУ – задающее устройство;

БРП – блок регулируемого привода;

ДС – датчик скорости;

Д – двигатель;

КС – кинематическая схема;

ДП – датчик перемещения.

В состав функциональной схемы входит система автоматического управления перемещением ИО – следящий привод подачи (СПП) и система автоматического регулирования (САР) скорости перемещения или скорости вращения. САР включает: Д, БРП и ДС. В состав СПП входит САР, КС и ДП.

Рассмотрим функциональную схему простейшей системы регулирования скорости (СРС), представленную на рис. 6. Эта система разомкнутого регулирования скорости.

Задающее устройство ЗУ определяет входной сигнал для системы управления СУ. СУ (усилитель мощности) управляет исполнительным двигателем постоянного тока Д.

Двигатель Д соединен с кинематической схемой КС. Выходным сигналом является угловая скорость вращения выходного вала КС.

Процесс управления угловой скоростью определяется следующей последовательностью.

1. Начальные условия. При отсутствии входного сигнала с ЗУ напряжения Uзу, так же отсутствует напряжение Uн и угловые скорости Ω1= 0 и Ω2 = O.

2. Включение. Напряжения Uзу = Uзуо, Uн = Uно и угловые скорости на входе и выходе КС по заданной траектории достигают значений Ω1= Ω1о и Ω1= Ω2о. В зависимости от характеристик нагрузки и системы управления могут возникнуть и колебания выходного сигнала.

3. Изменение нагрузки. При изменении момента сопротивления Мс = Мсо на выходном валу КС изменяется нагрузка и на входном валу КС, то есть на валу двигателя Д. Скорость Ω1 уменьшается, а для ее увеличения необходимо изменить сигнал с ЗУ и соответственно системы управления СУ.

Рассмотрим функциональную схему СРС с датчиком скорости ДС – рис.7. Это замкнутое регулирование скорости, которое называется системой автоматического регулирования (САР) скорости.

Процесс управления угловой скоростью определяется следующей последовательностью.

1. Начальные условия. При отсутствии входного сигнала с ЗУ напряжения Uзу, так же отсутствует напряжение Uн, угловые скорости Ω1 = 0 и Ω2 = O, сигнал с датчика скорости ДС Uдс = 0 и соответственно разностное напряжение Uзу – Uдс = 0.

2. Включение. Напряжение Uзу = Uзуо и Uн = Uно, так как угловые скорости на входе и выходе КС в начальный момент Ω1 = 0 и Ω2 = O и сигнал с ДС Uдс = 0. Двигатель Д разгоняется по заданной траектории, напряжение Uдс увеличивается, а разностное напряжение достигает установившегося значения Uзу – Uдс = *Uно. Скорости вращения входного и выходного вала КС достигают значений Ω1= Ω1о и Ω2 = Ω2о.

3. Изменение нагрузки. При изменении момента сопротивления Мс = Мсо на выходном валу КС изменяется нагрузка и на входном валу КС, то есть на валу двигателя Д.

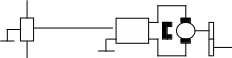ЗУ СУ Д КС

Uн

Uзу Ω1

Ω2

Рис. 6. Система регулирования скорости

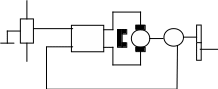ЗУ СУ Д ДС КС

Uзу Uн Ω1

Ω2

Uдс

Рис. 7. Система автоматического регулирования скорости

Скорость Ω1 уменьшается, уменьшается и напряжение Uдс, а разностное напряжение *Uн увеличивается. Двигатель Д за счет повышения напряжения Uн с выхода системы управления СУ увеличивает скорость, возвращая ее в исходное заданное значение Ω1= Ω1о.

При этом разностное напряжение *Uн уменьшается до значения *Uно.

Таким образом, САР скорости в автоматическом режиме отрабатывает увеличение нагрузки, возвращая значение выходного сигнала в исходное. САР скорости работает как система стабилизации скорости.

Лекция № 2

1. Виды уравнений

2. Математическое описание элементов систем

3. Временные характеристики – переходные процессы

1. Рассмотрим техническую систему, работающую в режиме включения/выключения, в этом случае в момент включения и выключения наблюдается изменение выходного сигнала, а при постоянном задании входного сигнала с течением времени наблюдается постоянное значение выходного сигнала.

Эти режимы работы описываются двумя видами уравнений:

уравнения для установившихся режимов работы – уравнения статики;

уравнения для переходных режимов работы – уравнения динамики, описывающие изменяющиеся процессы в элементах и системе в целом.

Для системы, когда на входе и выходе каждого элемента существует постоянное значение Х и У, записывается уравнение статики:

Ууст = К*Хуст,

где Хуст,Ууст – установившееся значение входного и выходного сигнала; К – коэффициент передачи.

Уравнение статики описывает статическую характеристику, которая является линейной зависимостью.

Уравнение динамики – это дифференциальное уравнение (ДУ) с постоянными коэффициентами, которое описывает процессы в механических, электромеханических и электрических цепях технической системы УЧПУ – МРС.

Уравнения динамики представлены 3 – мя формами:

1. Классическая.

2. Операторная.

3. Операционная.

Классическая форма ДУ в качестве переменной имеет текущее время t, в функции которого задаются входные и вычисляются выходные сигналы.

Операторная форма – это уравнение, где переменной является оператор p = d/dt.

Операционная форма аналогична формально операторной форме, где в качестве переменной s = p.

При моделировании любое ДУ стараются свести к стандартной форме записи, где выходной сигнал и его производные расположены в левой части, а входной сигнал – в правой части.

Представим две наиболее часто встречающиеся стандартные формы ДУ 1-го и 2-го порядков:

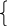T*dy(t)/dt + y(t) = k*x(t)

T²*d²y(t)/dt² +2*Dо T*dy(t)/dt + y(t) = k*x(t)

где k – коэффициент передачи; Т – постоянная времени; Dо – коэффициент демпфирования; х(t), у(t) – входной и выходной сигналы в функции времени.

Если в технической системе возникают переходные процессы по у(t), то dy(t)/dt – скорость изменения выходного сигнала, d²y(t)/dt² – ускорение.

Константа Т характеризует инерционность переходных процессов. Константа К определяет установившееся значение выходного сигнала. Константа Dо определяет величину колебаний выходного сигнала относительно установившегося значения.

Операторная форма записи уравнения записывается при замене р = d/dt

T*р*Y(р) + Y(р) = k*X(р)

T²*р²*Y(р) +2*Dо*T*р*Y(р) + Y(р) = k*X(р).

В этом случае получено алгебраическое уравнение, где X(р),Y(р) – условное обозначение входа и выхода и р – переменная (оператор). Из операторной формы можно получить математическую модель (ММ), которая называется передаточной функцией (ПФ)

W(р) = Y(р)/X(р).

Выше приведенные уравнения дают следующие передаточные функции

W(р) = k / (T*p + 1)

W(р) = k /(T²*р² +2*Dо*T *р + 1).

В ТАУ для известных стандартных форм ПФ известны уравнения и графики переходных процессов.

2. Рассмотрим математическое описание элементов, входящих в состав систем регулирования скорости и регулирования перемещения. Разбиение системы на элементы определяется ее функциональной схемой.

Кинематическая схема представляется единым редуктором, при этом в различные виды механических передач являются абсолютно жесткими.

Математическое описание редуктора при различных входных и выходных сигналах определяется следующим образом.

Рассмотрим условное обозначение редуктора, представленное на рис. 8 с указанием вида входных и выходных сигналов, то есть скорости Ω(t) или перемещения Ψ(t).

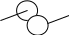
Ω1(t)

Ψ1(t) Ω2(t)

Ψ2(t)

Рис. 8. Условное обозначение редуктора

Для входного сигнала х(t) = Ω1(t) – скорость, выходного сигнала у(t) = Ω2(t) – скорость уравнение записывается:

Ω2(t) = К*Ω1(t).

Для входного сигнала х(t) = Ω1(t) – скорость, выходного сигнала у(t )= Ψ2(t) – перемещение уравнение записывается:

Ψ2(t) = К*∫Ω1(t)dt

Для входного сигнала х(t ) = Ψ1(t) – перемещение, выходного сигнала у(t ) = Ω2(t) – скорость уравнение записывается:

Ω2(t) = К*d Ψ1(t)/dt.

В операторной форме уравнения редуктора для трех случаев вида входа и выхода определяется следующими формулами

Ω2(р) = К*Ω1(р)

Ψ2(р) = К/р *Ω1(р)

Ω2(р) = К*р * Ψ1(р).

Математическая модель редуктора в виде ПФ (или ММ) определяется по формулам

W(p) = Ω2(р)/ Ω1(р) = K

W(p) = Ψ2(р) / Ω1(р) = K*1/p

W(p) = Ω2(р)/ Ψ1(р) = K*p.

Во втором случае 1/р = ∫ - символ интегрирования, в третьем случае переменная р = d /dt – символ дифференцирования.

В состав системы регулирования скорости для измерения скорости входит датчик скорости ДС.

ДС является тахогенератор постоянного тока.

На рис.9 представлено условное изображение датчика скорости ДС.

Ω1(t) Uдс(t)

Рис. 9. Датчик скорости

Входным сигналом ДС является скорость Ω1(t), а выходным – напряжение Uдс(t).

Уравнения для ДС записывается

Uдс(t) = Кдс*Ω1(t).

Уравнения в операторной форме

Uдс(р) = Кдс*Ω1(р).

Передаточные функции определяются

Wдс(р) = Uдс(р)/ Ω1(р) = Кдс.

Регулятор скорости РС представляет собой маломощный электронный усилитель с изменяемыми коэффициентами передачи Крс.

Уравнения РС записывается

Uрс(t) = Крс* Uзс(t)

где Uзс(t) – входной сигнал; Uрс(t) – выходной сигнал.

Передаточная функция РС определяется по формуле

Wрс(р) = Uрс(р)/ Uзс(р) = Крс

2. Исследование технических систем производится с целью получения определенных параметров временных процессов при управлении.

Анализ временных процессов в технической системе основан на использовании построенных переходных h(t) и импульсных переходных характеристик w(t).

Если на вход системы подается стандартный единичный ступенчатый сигнал вида 1(t), то на выходе появляется переходная характеристика h(t).

Если на вход системы подается дельта импульс вида δ(t), то на выходе появляется импульсная переходная характеристика w(t).

Рассмотрим определение временных характеристик для ММ редуктора, подставляя в уравнения типовой входной сигнал и переходные характеристики.

В этом случае переходные характеристики определяются по формулам

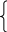
h1(t) = К*1(t)

h2(t) = К*∫1(t)dt = К*t

h3(t) = К*d 1(t)/dt.

На рис. 10 представлены временные диаграммы переходных характеристик h(t) с момента времени t1 для редуктора с соответствующими ММ.

Переходные характеристики ДС, СУ и РС аналогичны переходным характеристикам редуктора Р при соответствующих входных и выходных сигналах.

Лекция 3

1. Математическое описание двигателя

2. Типовые звенья в моделировании

3. Переходная характеристика технических систем

1. Рассмотрим в качестве двигателя постоянного тока (ДПТ) – двигатель с возбуждением от постоянных магнитов. Управление ДПТ осуществляется по одной цепи – цепи якорной обмотки с помощью подводимого напряжения от источника питания.

На рис. 11,12 представлены условное обозначение и схема замещения ДПТ схема замещения с указанием скорости вращения Ω1(t), момента сопротивления Мс(t), сопротивления якорной обмотки Rя, индуктивности Lя, мгновенного значения тока iя(t),наводимой э.д.с. E(t) и напряжения Uн(t).

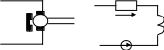Rя

Ω1(t)

iя(t)

Uн(t) Uн(t) Lя

E(t)

Рис. 11. Условное обозначение Рис. 12. Схема замещения

Используя уравнения Кирхгофа для электрических цепей и уравнения моментов для электромеханических цепей для ДПТ, запишем

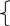
Мд(t) = Мн(t) – Мс(t)

Uн(t) = iя(t)*R + L*d/dt iя(t) + E(t).

В соответствии с принятыми обозначениями входа X и выхода Y необходимо получить уравнение, где вход – напряжение Uн(t), а выход – угловая скорость Ω1(t). Принимаем значение момента нагрузки Мс = 0.

Значение э.д.с. E(t) и значение электромагнитного номинального момента Мн(t) определяется

E(t) = Се* Ω1(t)

Мн(t) = См* iя(t).

Из уравнения моментов определяем значение тока

iя(t) = Jн/См *d Ω1(t) /dt.

Записываем окончательное уравнение по закону Кирхгофа при замене в нем значения полученного тока iя(t). дополнительно поделив его слагаемые на величину Се и добавив в числитель и знаменатель при производной d²Ω1(t)/dt² значение сопротивления Rя, при этом выходная величина записывается в левой части, а входная в правой части

JнRя/СмСе*Lя/Rя*d²Ω1(t)/dt² + JнRя/СмСе*dΩ1(t)/dt +

+ Ω1(t) = 1/Се*Uн(t).

Производим замену р = d/dt и получаем уравнение в операторной форме.

При этом вводим обозначения механической постоянной времени Тм = JнRя/СмСе, электрической постоянной времени Тэ = Lя/Rя и коэффициента передачи Кд =1/Се.

Преобразованное уравнение в операторной форме выражается

Тм*Тэ*р²* Ω1(p) + Тм*р* Ω1(p) + Ω1(p) = Кд* Uн (p).

Передаточная функция ДПТ определяется

W(p) = Кд/( Тм*Тэ*р² + Тм*р + 1) = Ω1(p)/Uн(p).

Если принять значение постоянной времени Тэ = 0, то ММ ДПТ определяется по формуле

W(p) = Кд/( Тм*р + 1).

При отсутствии переходных процессов, то есть значения d/dt = 0 и d²/dt² = 0, получаем установившийся режим работы ДПТ

Ω1= Кд*Uн,

где Ω1 – установившееся значение скорости вращения ДПТ;

Uн – значение напряжения.

2. В теории автоматического управления вводится понятия типовых динамических звеньев (ТДЗ). ТДЗ – это типовые математические модели, дифференциальные уравнения которых порядка не выше 2 – го.

Все ТДЗ разбиты на три класса.

Интегрирующие звенья:

W(p) = К/р – интегрирующее звено,

W(p) = К*( Тм*р + 1)/p – изодромное звено.

Основное свойство выходного сигнала: y(t = ∞) = ∞.

Дифференцирующие звенья.

W(p) = К*р – интегрирующее звено,

W(p) = К*( Тм*р + 1) – форсирующее звено.

Основное свойство выходного сигнала: y(t = 0) = ∞, а при y(t>0) = 0.

Позиционные звенья

W(p) = К – пропорциональное,

W(p) = К/(Т*р + 1) – апериодическое,

W(p) = К/( Т²2*р² +Т1*р + 1) – апериодическое 2-го порядка,

W(p) = Кд/( Т²*р² +2*Do*Т*р + 1) – колебательное.

Основное свойство выходного сигнала позиционных звеньев:

y( t = ∞) = Ууст = К*Хуст,

где Хуст, Ууст – установившееся (постоянное значение) входного и выходного сигналов.

3. Для анализа технических систем вводятся параметры качества регулирования, которые определяют быстродействие системы точность, наличие скорости и ускорения в переходном процессе.

На рис. 13 представлена переходная характеристика и выполнены дополнительные построения для определения параметров качества регулирования.

К основным показателям качества регулирования относятся: допустимое отклонение Δ, время регулирования tр; характеристика величины колебательности σ.

Значение колебательности оценивается по формуле:

σ = (σмак – σуст)/σуст * 100%.

Для технических систем допустимое отклонение задается Δ = ± 0,05*hуст.

В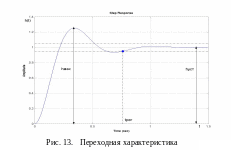 ремя регулирования определяется по графику переходной характеристики, как последнее касание верхней 1,05*hуст или нижней 0,95*hуст границ запретной зоны для допустимого отклонения.

При проектировании технических систем указывается вид переходного процесса и его параметры качества регулирования.

Коэффициент передачи К влияет на установившееся значение hуст, постоянная времени – на значение времени регулирования tр и коэффициент демпфирования Do – на характеристику колебательности.

В ТАУ технические системы изображаются графически в виде структурных схем. Структурная схема – это графическое изображение функциональной схемы системы с сохранением связей между элементами, где каждый элемент представлен ПФ.

Каждая СХ состоит из основных частей:

элемент сравнения

л иния связи

э лемент схемы

Все элементы в структурной схеме соединены последовательно, параллельно и с обратной связью ( встречно – параллельное соединение ).

Рассмотрим структурную схему САР, полученную из приведенной функциональной схемы системы УЧПУ-МРС.

В зависимости от ММ двигателя постоянного тока существует несколько структурных схем САР скорости.

На рис. 14 САР скорости включает ММ регулятора скорости Wрс(р), ММ системы управления Ксу, ММ датчика скорости Кдс и ММ ДПТ Wд(p), как апериодического звена (А-звена).

Wрс(p) Wсу(p) Wд(p) X У

Крс Ксу К / (Т p + 1)

-

Wдс(p)

Кдс

Рис. 14. Структурная схема САР скорости с двигателем А - звеном

На рис. 15 САР скорости включает ММ регулятора скорости Wрс(р), ММ системы управления Ксу, ММ датчика скорости Кдс и ММ ДПТ Wд(p), как колебательного звена (К-звена).

Wрс(p) Wсу(p) Wд(p) X У

Крс Ксу К / (Т² p² + 2 DoТ p + 1)

-

Wдс(p)

Кдс

Рис. 15. СХ САР скорости с двигателем К-звеном

Представленные структурные схемы САР скорости методом преобразования можно упростить и свести к ТДЗ.

Для структурной схемы САР скорости с двигателем А-звеном ММ выражается

Wсар(p) = Ко/ (То*р + 1),

где Ко = Крс*Ксу*К/(1 + Крс*Ксу*К*Кдс) – коэффициент передачи; То = Т/(1 + Крс*Ксу*К*Кдс) – постоянная времени.

Для структурной схемы САР скорости с двигателем К-звеном ММ выражается

Wсар(p) = Ко / (Т²о p² + 2 DoоТо p + 1),

где Ко = Крс*Ксу*К/(1 + Крс*Ксу*К*Кдс) – коэффициент передачи; То = Т/ √( 1 + Крс*Ксу*К*Кдс) – постоянная времени;

Dоo = Do/√(1 + Крс*Ксу*К*Кдс) – коэффициент демпфирования.

Для структурной схемы САР скорости с двигателем А-звеном переходная характеристика определяется выражением

-t/Tо

h(t) = Kо ( 1 - е ).

Значения переходной характеристики определяются по точкам t = 0, t = To, t = 2To, t = 3To.

Для структурной схемы САР скорости с двигателем К-звеном переходная характеристика определяется

-αt

h(t) = Ко ( 1 - K1 е sin ( β t + Ψ ).

Обычно в САР скорости изменяемым параметром является коэффициент передачи регулятора скорости Крс.

Для САР скорости с двигателем А-звеном при увеличении коэффициента Крс постоянная времени То уменьшается и следовательно время регулирования уменьшается, а быстродействие увеличивается.

На рис. 16 представлены три вида переходных характеристик апериодических первого порядка при изменении коэффициента Крс.

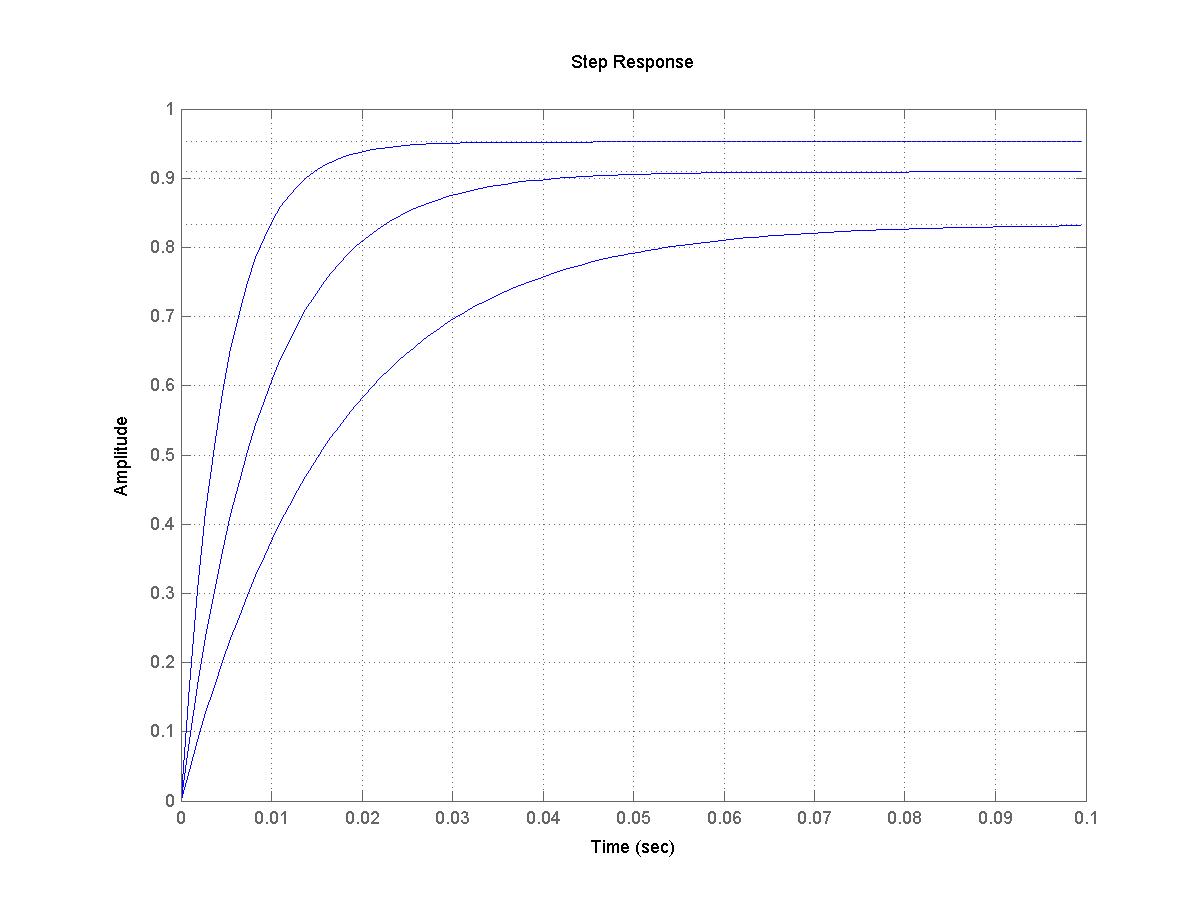
Рис. 16. Переходные характеристики САР скорости

Для САР скорости с двигателем К-звеном при увеличении коэффициента Крс уменьшается постоянная времени То и уменьшается коэффициент демпфирования Doo.

Время регулирования tp за счет увеличения колебательности увеличивается.

При значительном уменьшении Крс постоянная времени системы То равняется постоянной времени двигателя Т и коэффициент демпфирования Doo системы – коэффициенту демпфирования двигателя Do.

В этом случае переходная характеристика системы равняется переходной характеристике ДПТ. Время регулирования системы увеличивается и равняется времени регулирования ДПТ в разомкнутой системе.

На рис. 17 представлены два вида переходных характеристик САР скорости с двигателем К-звеном.

Рис. 17. Два вида переходных характеристик

Установившееся значение переходной характеристики САР скорости при значительном увеличении коэффициента Крс определяется Ко =1/Кдс.

Время регулирования для САР скорости с двигателем К-звеном и получении типовой переходной характеристики h(t) определяется tр = 3,55*То.

Для получения типовой переходной характеристики в САР скорости с двигателем К-звеном необходимо воспользоваться тем, что коэффициент демпфирования ММ системы должен равен Dоo = 0.707.

Используем значения коэффициентов К и Т в структурной схеме САР скорости и значение коэффициента демпфирования двигателя, как колебательного звена

Dоo = Do/√(1 + Крсо*Ксу*К*Кдс)

Do = 1/2*√Тм/Тэ.

Отсюда требуемое оптимальное значение коэффициента передачи регулятора скорости Крсо определяется:

Крсо = (1/4* Тм/Тэ*1/[0,707]² - 1)*1/[Ксу*К*Кдс.

При задании значения Крсо в САР скорости с двигателем типом динамическим звеном 2-го порядка, переходная характеристика на выходе системы оптимальная по быстродействию.

Контрольная работа 1

Математические модели элементов системы автоматического регулирования скорости