
тмиэт / Экзамен Тмеет / тмиэт / Лекции ТМиЭЭТ_ тема_2
.pdf
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»,
кафедра физической электроники и технологии
Профессор Шаповалов Виктор Иванович Доцент Никитин Андрей Александрович
ТЕХНОЛОГИЯ МАТЕРИАЛОВ И ЭЛЕМЕНТОВ ЭЛЕКТРОННОЙ ТЕХНИКИ
Тема 2
Литература
1)Аброян И.А., Андронов А.Н., Титов А.И., Физические основы электронной и ионной технологии: Учеб. пособие для спец. электронной техники вузов. – М.: Высш.шк., 1984. – 320 с.
2)Альфорд Т.Л., Фельдман Л.К., Майер Д. В. Фундаментальные основы анализа нанопленок / Пер. с англ. Образцов А.Н., Долганов М.А., науч. ред. Образцов А.Н. - М.: Научный мир, 2012. - 392 с.
3)Корпускулярно-фотонная технология : учеб. пособие для вузов по спец. «Промышленная электроника» / О. Г. Вендик, Ю. Н. Горин, В. Ф. Попов. - М. : Высш. шк., 1984. - 240 с.
4)Попов В.Ф., Горин Ю.Н. Процессы и установки электронно-ионной технологии. – М.: Высш.шк., 1988. – 255 с.
5)Григорьянц А.Г., Шиганов И.Н., Мисюров А.И. Технологические процессы лазерной обработки / под. ред. А.Г. Григорьянца. М.: из-во МГТУ им. Н.Э. Баумана, 2006.- 664 с.
6)Светцов В.И., Смирнов С.А. Корпускулярно-фотонные процессы и технологии: учеб. пособие / Иван. гос. хим.-технол. ун-т Иваново. 2009. – 277 с.
7)Либенсон М.Н., Яковлев Е.Б., Шандыбина Г.Д. Взаимодействие лазерного излучения с веществом (силовая оптика). Конспект лекций. Часть I. Поглощение лазерного излучения в веществе. Под общей редакцией В.П. Вейко – СПб: СПб ГУ ИТМО, 2008. – 141 с.
8)Ландау Л.Д., Лифшиц Е. М. Курс теоретической физики: Учеб. пособ.: Для вузов. В 10 т. Т. III. Квантовая механика (нерелятивистская теория). - 6-е изд., испр. - М.: ФИЗМАТ ЛИТ, 2004. - 800 с.
9)А.П. Менушенков, В.Н. Неволин, В.Н. Петровский Физические основы лазерной технологии. М.: НИЯУ МИФИ, 2010, 212 стр.
Данные для расчета коэффициента распыления
1)Sputtering by Particle Bombardment /Eds Rainer B.,Wolfgang E. – Springer-Verlag Berlin Heidelberg 2007. 557 c.
1
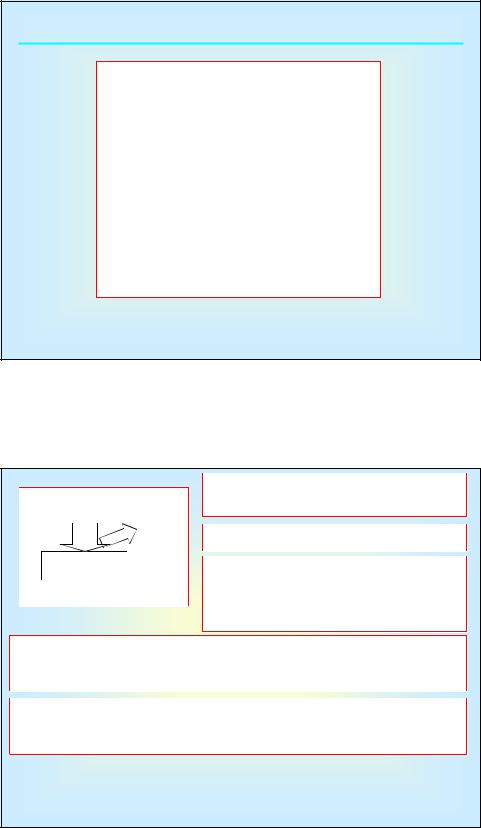
Тема 2. ВЗАИМОДЕЙСТВИЕ КОНЦЕНТРИРОВАННЫХ ПОТОКОВ ЭНЕРГИИ С ТВЕРДЫМ ТЕЛОМ
Содержание
2.1.Взаимодействие ускоренных электронов с твердым телом
2.1.1.Торможение электрона
2.1.2.Пробег
2.1.3.Применение электронного пучка
2.2.Взаимодействие ионов с твердым телом
2.2.1.Потери энергии
2.2.2.Пробег иона
2.2.3.Дефекты
2.2.4.Физическое распыление мишени
2.2.5.Применение ионного пучка
2.3.Взаимодействие фотонов с твердым телом
2.3.1.Механизмы поглощения фотонов
2.3.2.Нагрев объемного материала
2.3.3.Нагрев пленки
КПЭ q, Вт/м2
Q Qотр
Qпогл Мишень
Qпогл = QT + QA(+,0,*) + Qe
Концентрированные потоки энергии (КПЭ) – ускоренные в электрическом поле электроны или ионы, а также или фотоны, генерируемые лазером.
Q = Qотр + Qпогл
Qотр = Qhν + QA( +,0,*) + Qe
Отраженную энергию уносят во внешнюю среду частицы и фотоны.
Технологическая процессы: распыление, испарение.
Поглощенная энергия расходуется на возбуждение и ионизацию, генерацию дефектов, нагрев мишени (плавление, кипение, перестройка кристаллической структуры, химические реакции, имплантация).
1)мягкий режим: q < 109 Вт/м2 - скорость тепловыделения < скорости отвода тепла из зоны нагрева за счет теплопроводности материала мишени.
2)жесткий режим: q > 109 Вт/м2 - скорость тепловыделения ≥ скорости теплоотвода.
Большая часть энергии расходуется на разогрев зоны тепловыделения и выброс расплава из нее.
2
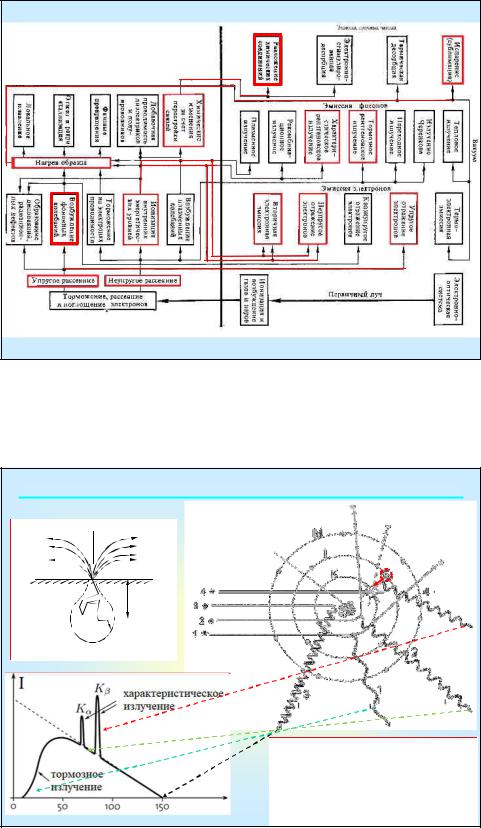
Твердое тело (мишень) |
|
2.1. Взаимодействие ускоренных электронов с твердым телом |
|||
|
E0 |
|
Электронные |
ВЭ |
|
|
|
||
ТРИ |
УЭ |
оболочки |
|
|
|
Ядро |
|
||
ХРИ |
|
ВЭ |
|
|
|
|
|
||
|
|
атома |
|
|
|
|
ОЭ |
|
|
КЛ |
|
|
|
|
|
ТЭ |
e |
|
|
|
|
|
||
|
|
|
|
|
|
|
Rp |
|
ХРИ |
|
|
R |
|
|
|
|
|
ТРИ |
|
|
|
|
ТРИ является результатом изменения |
|
|
|
|
скорости и направления движения e. |
|
|
|
|
ХРИ. В результате неупругого рассеяния e |
|
|
|
|
выбивается с одной из внутренних |
|
|
|
|
оболочек (K, L). e с верхних уровней (L,M) |
|
|
|
|
занимают освободившееся место. |
|
3
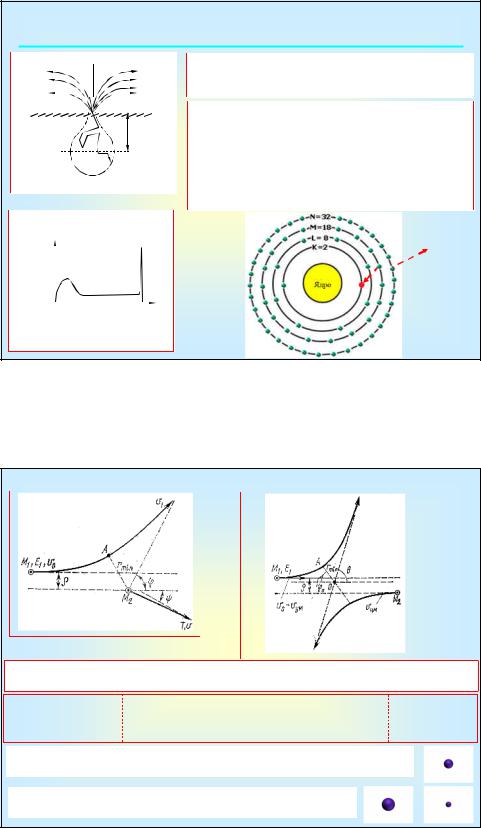
2.1. Взаимодействие ускоренных электронов с твердым телом
ТРИ E0 УЭ
ХРИ |
ВЭ |
|||
|
|
|||
КЛ |
ОЭ |
|||
ТЭ |
||||
|
|
|||
|
|
|
|
|
|
|
Rp |
||
|
|
R |
||
УЭ
dN/dE
ВЭ
ОЭ
0 ≈ 50 эВ |
E0 E |
Истинно вторичные электроны E < 50 эВ, большая часть E ~ 2-3 эВ. Их число может превышать число падающих на поверхность первичных ионов.
E > 50 эВ характерна для неупруго рассеянных электронов и оже-электронов. Рассмотрим подробнее оже-эффект. В результате неупругого рассеяния e выбивается с одной из внутренних оболочек (K). e с верхних уровней (M) занимают освободившееся место. Если выделяемая в результате энергия Ek-EM предаётся электрону расположенному на уровне N, то такой e будет в состоянии покинуть мишень.
ОЭ
|
|
Система координат |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лабораторная система |
|
|
|
Система координат |
|
|
|
координат |
|
|
|
центра масс |
|
|
|
M1, E,V0 |
|
|
|
M1, E,V0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
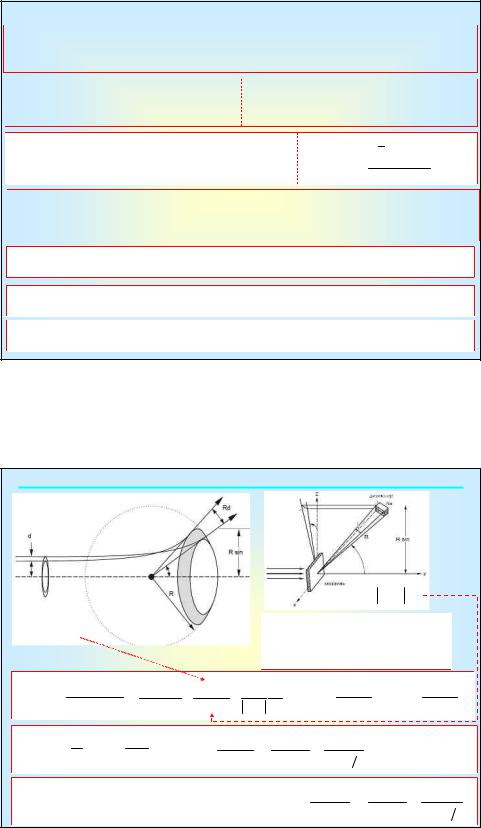
ρ – прицельный параметр (расстояние) – это расстояние, на котором М1 прошла бы мимо M2, если бы взаимодействие между ними отсутствовало. Центральное (лобовое) соударение ρ = 0.
|
M1V = M1V1 + M 2V2 |
Tm = |
4M1M 2 |
|
E |
Энергии, теряемая (передаваемая) |
γ = |
4M1M 2 |
|
|
|||||
|
M1V |
2 |
2 |
2 |
(M1 + M 2 ) |
2 |
налетающей частицей при лобовом |
(M1 + M 2 ) |
2 |
|
|||||
|
|
= |
M1V1 |
+ |
M 2V2 |
|
|
|
столкновении столкновении. |
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||
Наиболее эффективен обмен энергией при упругих соударениях между частицами со сравнимой массой.
При центральном столкновении частиц с существенно различной массой доля передаваемой энергии невелика.
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система координат |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∞ |
|
ρ |
|
|
ρ2 |
|
V (r) −1/2 |
|
|
|
|
|
||||
|
θ = π − 2 |
|
|
|
|
1 |
− |
|
|
− |
|
dr |
- угол отклонения частиц в системе координат центра масс |
|
||||||
|
|
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
||||
|
|
|
|
r |
|
|
|
|
|
|
Eотн |
|
|
|
|
|
||||
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Eотн = |
|
M 2 |
|
|
E |
|
|
Энергия |
движущейся |
V (r) |
Потенциальная |
энергия |
|
||||||
|
M1 |
|
|
|
|
|
|
частицы в СК центра масс |
взаимодействия двух частиц |
|
||||||||||
|
|
|
+ M 2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = Tm sin2 θ |
Энергия, теряемая частицей в результате |
столкновения движущейся частицы в СК |
|
2 |
центра масс |
|
ψ = 1 (π − θ)
2
ϕ = sin θ tg
M1  M 2 + cos θ
M 2 + cos θ
M1<<M2 рассеяние электрона на атоме |
M1=M2 рассеяние двух одинаковых частиц |
||||||
ϕ = θ |
|
|
|
sin θ |
|
||
=> |
|
|
= E |
tgϕ = |
|
||
E |
|
|
+ cos θ |
||||
|
отн |
1 |
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Пусть частицы в пучке имеют одинаковую начальную скорость (энергию), но различное прицельное расстояние => они рассеиваются под различными углами ϴ в СК центра масс.
Пусть dN – число частиц, рассеивающихся на углы в диапазоне от ϴ до ϴ+dϴ. Тогда характеристика dN связана с плотностью падающего пучка N выражением dN=Ndσ.
Дифференциальное сечение рассеяния dσ=dN/N описывает вероятность рассеивания в определённом направлении.
|
|
|
|
|
|
|
|
Дифференциальное сечение рассеяния |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
Δψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Δϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ρ |
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
d Ω = 2π sin ϕ dϕ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
d σ = 2πρdρ |
|
|
|
|
|
|
|
|
|
|
|
dσЛСК |
|
|
|
микроскопическое |
|
сечение |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
рассеяния описывает |
число |
частиц |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dN=Ns(φ,ψ)dΩ, рассеянных внутри |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
телесного угла dΩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
d σЛСК = |
Ns (ϕ,ψ)d Ω |
N |
s |
(ϕ, ψ) |
= |
d σ |
|
= |
ρ dρ |
|
|
|
F (r ) |
= |
Z Z |
2 |
e2 |
=>V (r ) = |
Z Z |
2 |
e2 |
→ |
|||||||||||||||||
|
|
N |
|
|
|
|
|
|
ЛСК |
|
|
|
|
|
|
|
1 |
|
2 |
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
d Ω |
sin ϕ d ϕ |
|
|
|
|
|
4πε0r |
|
|
|
|
4πε0r |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
θ = π − 2 |
∞ |
ρ |
|
ρ2 |
− |
V (r) |
−1/2 |
|
|
d σЦМ |
= |
|
Z Z |
2 |
e2 2 |
|
|
1 |
|
|
|
|
|
|
|
Формула |
|
|
|
|
|||||||||
|
|
2 |
1 − |
|
2 |
|
|
dr |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
r |
|
r |
|
|
|
|
|
|
|
d Ω |
|
|
16πε |
|
|
E |
|
|
4 |
|
|
|
|
|
|
Резерфорда |
|
|||||||||||
|
r |
|
|
|
|
Eотн |
|
|
|
|
|
0 |
sin |
θ 2 |
|
|
|
|
|||||||||||||||||||||
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для электронов, рассеивающихся на атомах (M1<<M2): |
|
|
|
d σ |
ЛСК = |
|
Z Z |
2 |
e2 |
2 |
|
1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dΩ |
|
|
|
|
16πε0E |
|
sin |
ϕ 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5
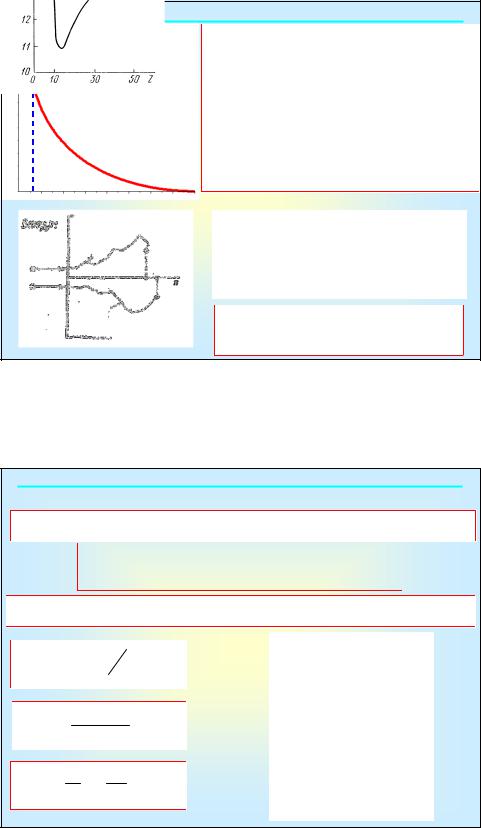
2.1.1. Торможение электрона
dσ/dΩ
Сечение рассеяния электронов при малых значениях ϴ
sin-4(ϴ/2)
ϴ* |
|
|
|
|
Твердое тело (мишень) |
||
Вакуум |
|||
|
dl |
Rl2 |
|
Eн,M1 |
|||
|
|||
Rp2
Rp1
Rl1
d σЛСК |
|
→ ∞ |
|
||
d Ω |
|
|
|
θ→0 |
|
|
В результате использования классического приближения (частица, проходящая на любом конечно расстоянии будет рассеиваться на некоторый малый, но отличный от нуля угол). Классическое приближение справедливо при ϴ> ϴ*
θ* = |
λ |
, где λ = |
h |
, a = 0.885a0 (Z11/2 + Z |
21/2 )2/3 |
|
|
||||
2πa |
M1v |
|
|||
a0 = 0.53∙10–10 м – радиус ближайшей к ядру орбиты электрона в атоме водорода (боровский радиус)
ϴ h=6,626 10−34 кг·м2·с−1
π
Среднее значение энергии, переданное веществу частицей на элементарном пути.
dE |
|
Eн |
|
= −N |
Ed σ |
||
|
|||
dl |
Emin |
||
|
|
||
При движении электронов в веществе их энергия непрерывно уменьшается в результате неупругих столкновений (ионизация, возбуждение), а траектория изменяется в результате их упругого рассеяния на атомах.
2.1.1. Торможение электрона
Уравнение Бете
Уравнение Бете впервые получено для неупругого рассеяния заряженных частиц на атомах водорода.
|
dE |
= − |
2πn e4 |
|
|
bE |
||
|
|
e |
|
|
ln |
|
|
|
|
dl |
(4πε0 ) |
2 |
E |
ˆ |
|
||
|
|
|
|
I |
||||
E – энергия, кэВ; e = 1.602∙10–19 Кл; I – средняя энергия возбуждения атома мишени, кэВ; ne – концентрация электронов, см–3 ; b = 1.166 обеспечивает применимость для Z>1.
ε = bE
I
ξ = 2πneb2e4 l = Kl
(4πε0 I )2
dε = − ln ε dξ ε
6
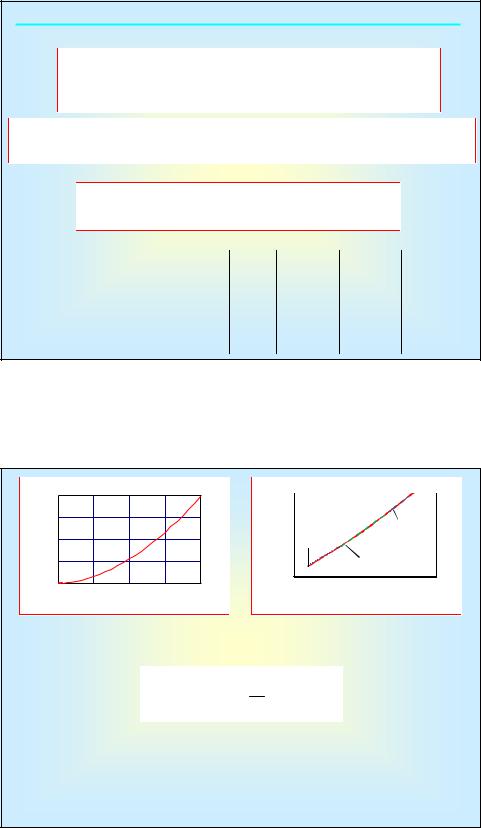
2.1.2. Пробег
Траекторный пробег:
|
εmin d ε |
−1 |
εн εd ε |
Li (εн2 ) |
||||
|
|
|||||||
rξ |
|
|
|
|
d ε = |
|
|
|
|
ln ε |
|||||||
|
d ξ |
|
|
|||||
|
εн |
|
|
|
|
εmin |
|
|
Так как торможение электронов является результатом ионизации или возбуждения атомов, то минимальная энергия электрона в конце пути должна соответствовать минимальной энергии возбуждения атома
Аппроксимация: |
|
|
|
|
d ε |
1 |
|
rξ kεнn |
|
− |
|
d ξ |
knεn−1 |
||
Li(x) –
Интегральный
логарифм
Emin 0.6I
Диапазон εн |
1 – 10 |
5 – 50 |
10 – 100 |
50 – 500 |
|
100 – 1000 |
500 – 5000 |
1000 – 100 |
00 |
|
|
|
|
|
|
|
|
|
|
n |
1.35 |
1.52 |
1.64 |
1.77 |
|
1.80 |
1.85 |
1.865 |
|
|
|
|
|
|
|
|
|
|
|
k |
1.37 |
0.95 |
0.64 |
0.36 |
|
0.31 |
0.223 |
0.198 |
|
|
|
|
|
|
|
|
|
|
|
Максимальная |
5 |
5 |
3.5 |
3 |
|
2 |
1 |
0.5 |
|
погрешность, % |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rξ, |
|
|
|
|
rξ |
|
|
|
|
104 |
|
|
|
|
|
|
|
||
|
|
|
|
1000 |
|
|
|
||
6 |
|
|
|
|
|
100–1000 |
|||
|
|
|
|
|
100 |
|
|||
4 |
|
|
|
|
1–10 |
|
|
||
2 |
|
|
|
|
10 |
|
10–100 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
10 |
100 |
ε |
||
0 |
250 |
500 |
750 |
ε |
|||||
|
|
|
|
||||||
Размерный траекторный пробег:
Rl = rξ
K
7
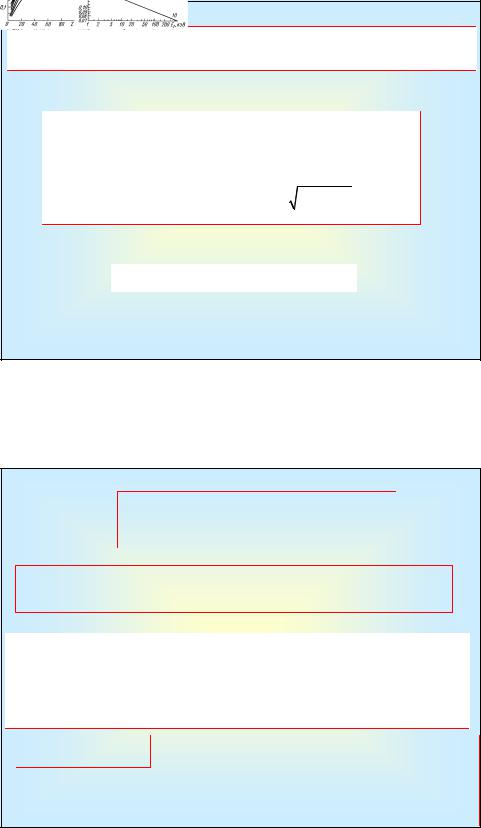
С точки зрения решения практических задач более важно знать усредненные значения энергетических потерь по всем частицам падающего на поверхность пучка электронов в направлении нормали к поверхности.
Уравнение Виддингтона-Томсона:
d ε |
1 |
|
|
|
n = 2 |
|
d ε |
− |
1 |
|||
|
|
|
|
|
|
|||||||
d ξ |
− |
knεn−1 |
|
|
|
|
d ξ |
|
|
2knε |
||
|
|
|
dE |
|
ρb1 |
|
|
|
|
|
|
|
|
|
− |
|
|
2 |
|
|
|
||||
|
|
|
|
2E |
E( x) |
E0 |
− ρb1x |
|
||||
|
dx |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
b1 » (0.476 -1.24 ×10−3 Z ) ×106
I Способ:
|
|
|
0 |
dE |
−1 |
|
E02 |
|
3 |
|
|
|
||||
|
|
|
R p = |
|
dx |
|
dE == |
ρb |
см, ρ [г / см |
|
] E0 |
[кэВ] |
|
|||
|
|
|
E |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II Способ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||||||||
|
R p ≈ |
0.0276ME01.67 |
мкм, |
M [г/моль], E0 [кэВ], ρ [г/см3 ] |
||||||||||||
|
|
|||||||||||||||
|
|
|
ρZ 0.889 |
|
|
|
|
|
|
|
|
|
|
|
|
|
III Способ:
Физически ясно, что существует прямая пропорциональность между траекторным и проекционными пробегами. Коэффициент пропорциональности должен определятся процессами рас-сеяния электронов в веществе. Одним из подходов является использование коэффициента неупругого отражения (рассеяния) электронов η, значения которого известны для большого числа веществ в широком диапазоне энергий. Анализ экспериментального материала показывает, что в для проекционного пробега независимо от материала мише-ни и энергии электронов справедлива приближенная фор-мула:
|
R p |
= Rl (0.95 − 1.1η) |
|
|
|
|
Для |
|
E > |
5 |
|
|
|
|
|
кэВ |
η слабо |
||||
|
|
|
|
|
|
|
зависит |
от |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
|
η – |
отношение числа вторичных |
|
|
|
энергии. |
|
|||
|
электронов с энергиями, большими 50 |
|
|
|
η = |
|
Z − 8 |
|
||
|
эВ, к числу первичных электронов. |
|
|
|
|
|
||||
|
|
|
|
|
2Z |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
|
|
Твердое |
|
|
|
|
|
|
|
||
|
|
|
Вакуум |
|
|
|
тело |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J0,Eн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область |
||
|
Электронный |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Область |
|
|
|
|
|
рассеяния на |
|||||||||||
|
|
|
луч |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
большие углы |
|||||||||||
|
|
|
|
|
рассеяния на |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
малые углы |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E( x) E |
2 |
−ρb x |
|
− |
dE |
|
ρb1 |
|||||||||||||
0 |
1 |
|
|
|
|
|
2E |
|||||||||||||
|
|
|
|
dx |
||||||||||||||||
|
|
|
|
dE |
|
|
|
|
|
|
|
dE |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
, E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dx |
|
|
|
|
|
|
|
dx |
|
|
|
|||||
Eн
Упрощенное рассмотрение:
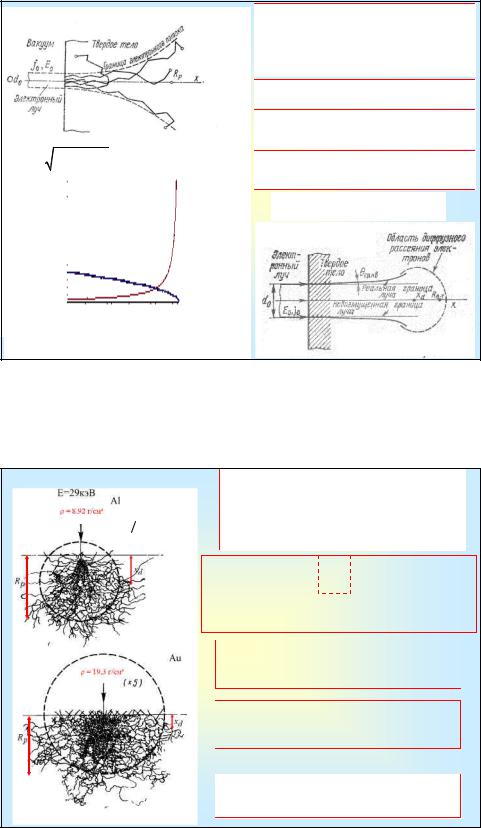
Отклонение направления движения электрона (рассеяние пространстве на определенный угол), обусловлено упругими столкновениями Потери энергии электроном связаны с неупругими столкновениями электрона и атома.
При высоких энергиях электрон испытывает большое количество актов рассеяния на малые углы
При малых энергиях e рассеяние происходит на большие углы (вплоть до π). Т.е. почти изотропное или диффузионное рассеяние электронов.
Глубина полной диффузии электронов, т.е. глубина, начиная с которой электроны двигаются диффузно (равновероятно во всех направлениях)
xd =12Rp  (Z + 8)
(Z + 8)
Rp |
|
J0,Eн |
|
Рост энергетических потерь физически связан с тем, что при уменьшении скорости электрона возрастает время взаимодействия с орбитальными электронами атома.
Диффузионная модель
|
|
Z=13 |
|
R p = |
E02 |
xd =12Rp (Z + 8) = 0.57Rp |
|
ρb |
|||
|
|||
|
1 |
|
Z=79
xd =12Rp  (Z + 8) = 0.14Rp
(Z + 8) = 0.14Rp
Все электронно-лучевые технологические процессы связаны с передачей энергии от электронов обрабатываемому материалу.
Q [Дж/м3] – объемная удельная энергия - энергия электронного пучка, выделяемая в единице объема; P [Вт/м3] – объемная удельная мощность.
Q( x) = |
dE Ne e τ |
|
|
dE |
1 |
|
||||||||
|
|
|
|
|
|
|
|
= |
|
|
j( x)τ |
|
|
|
dx S τ e |
|
dx |
e |
|
||||||||||
P( x) = |
dE |
|
j( x) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dx |
e |
|
|
|
|
|||||
|
|
|
|
dE j(x) |
|
j |
dE |
|
j |
|||||||||
|
Q(x) = |
|
|
|
|
|
|
|
τ |
0 |
= |
|
|
τ |
0 |
|
||
|
|
dx |
|
|
j0 |
e |
|
e |
||||||||||
|
|
|
|
|
|
|
|
|
dx эфф |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dE |
= |
|
dE j( x) |
|
|
Эффективные |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
энергетические потери |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
dx эфф |
|
|
|
dx |
|
|
j0 |
|
|
энергии электронов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введение эффективных энергетических потерь позволяет считать, что электронный луч не рассеивается при распространении в веществе.
9
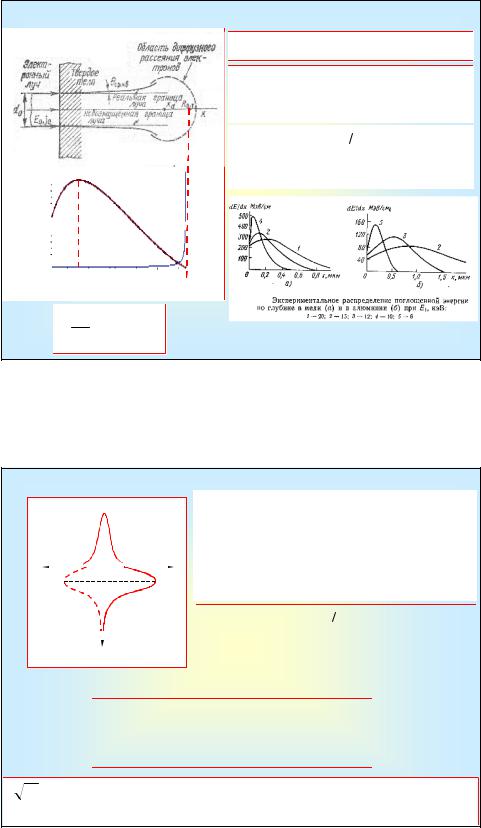
Энергия, выделяемая электронами пучка в единице объема вещества
j( x) = en( x)V ( x)
Скорость электронов уменьшается в результате торможения, концентрация изменяется за счет электронов, диффузно распространяющихся от xd к поверхности.
|
dE |
|
|
|
E |
0 |
|
|
x |
5 4 |
|
|
Z + 8 x |
||||||
|
|
= |
|
1 |
− |
|
|
|
|
3 |
− 2 exp − |
|
|
|
|
|
|||
|
|
|
|
R |
|
R |
|
4 R |
|
||||||||||
|
dx |
эфф |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
p |
|
|
p |
|
|
|
|
|
|
p |
||||
dE |
dE |
||
|
, |
|
|
dx |
|
||
|
dx эфф |
||
δ0 |
|
|
|
Rp |
|
|
|
δ0 = 0.2 − 0.4
Rp
Электронно-лучевой нагрев
Пусть на мишень направлен осесимметричный электронный луч с гауссовым распределением плотности
I(r) тока
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
j = |
|
i |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
r |
j (r) = |
j exp |
− |
|
|
|
|
0 |
πr02 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
T |
|
|
Tпов |
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
T |
|
|
|
|
|
|
|
|
|
r0 |
– эффективный радиус |
||||||||||||||||
|
м |
|
δ |
|
|
|
|
|
|
|
r0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электронного луча |
|
||||||||
|
|
|
|
|
PV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
r2 |
|
|
x |
5 4 |
|
|
|
Z + 8 x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
P |
= P exp |
|
|
1 |
− |
|
|
3 |
− 2 exp |
− |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
V |
|
|
0 |
r2 |
|
|
Rp |
|
|
|
|
|
4 Rp |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение теплопроводности (Фурье) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
∂T (x, y, z,t ) |
− a T (x, y, z,t ) = |
|
Pv (x, y, z ) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
ρc |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∂t |
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ρc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 at - характеризует размер разогретой области. Введем характерное время:
at - характеризует размер разогретой области. Введем характерное время:
τ = R2p  4a
4a
10
