
тмиэт / Экзамен Тмеет / 3
.pdf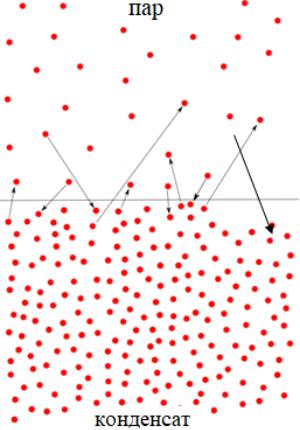
Метод МОС-гидридной эпитаксии основан на взаимодействии металлоорганических соединений (МОС) с гидридами элементов арсин AsН3, фосфин PН3 и др.
Металлоорганические соединения имеют химические связи типа металл– углерод, например, метиловые или этиловые соединения, такие как:
•метилнатрий CH3Na,
•диметилцинк (CH3)2Zn,
•триметилгаллий (CH3)3Ga,
•тетраэтилсвинец (C2H5)4Pb.
Испарение веществ.
В основе процесса испарения лежит образование пара над поверхностью вещества.
Насыщенный пар – пар, который находится в равновесии с жидкостью или твердым телом того же состава.
Далее мы будем называть жидкость или твердое тело конденсированным состоянием. Соответственно, насыщенный пар находится в равновесии с конденсированным состоянием. Давление, при котором это выполняется, называется давлением насыщенного пара.
Это давление обычно описывается уравнением Антуана:
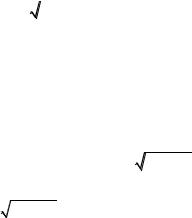
ln p = A − |
B |
(x26) |
|
C +T |
|||
Рисунок 43 – Испарение веществ |
|
||
|
|
Будем использовать его следствие – давление насыщенного пара возрастает с температурой и сильно зависит от нее.
На практике мы будем использовать более простую аппроксимацию:
|
p =133 10A− |
B |
|
lg p = A − B / T, p 1 Tорр, тогда |
T |
Па . |
31
Для того, чтобы получить уравнение, которое описывает скорость испарения, будем использовать два стартовых момента:
1. Скорость испарения пропорциональна давлению насыщенного пара. В первой теме было получено выражение для потока газа на стенку, ис-
пользуя уравнение для идеального газа и среднюю скорость:
|
|
|
|
|
|
|
|
|
|
|
|
J = |
nc |
= |
|
p |
|
|
1 |
|
|
- описывает количество атомов, которые сталкива- |
|
|
|
|
|
|
|
2 |
|
|
|||
|
4 |
|
|
2 mkT |
|
|
м |
с |
|
||
ются с 1 м2 поверхности за 1 секунду.
Герцем было доказано и экспериментально подтверждено, что максимальная скорость испарения пропорциональна числу атомов, которые сталкиваются с поверхностью в случае равновесия:
|
|
|
|
J0 = av |
p − p0 |
|
- уравнение Герца-Кнудсена, |
||
|
|
|
|
|
|
|
|||
|
|
|
|
2 mkT |
|||||
|
|
|
|
|
|
|
|
||
где |
|
p |
|
показывает число частиц, попадающих на поверхность; р – |
|||||
|
|
|
|||||||
|
|
|
|||||||
2 mkT |
|||||||||
|
|
|
|
|
|
|
|
||
равновесное давление (давление насыщенного); р0 – гидростатическое давление, т.е. давление столба, описывает число частиц, возвращающихся из газовой фазы в жидкость.
2. Это уравнение не всегда соответствует действительности (не для всех материалов), поэтому был введен коэффициент испарения av , который показывает отношение рассчитанной скорости к скорости установленной экспериментально.
Смысл его в том, что часть молекул со стороны газовой фазы отражается от поверхности и не участвует в испарении.
Таким образом, можно ввести уравнение Герца-Кнудсена, которое показывает максимально возможную скорость испарения с произвольной поверхности.
Давление насыщенного пара.
Рассмотрим графики, которые отражают зависимость давления пара от температуры для различных материалов.
32
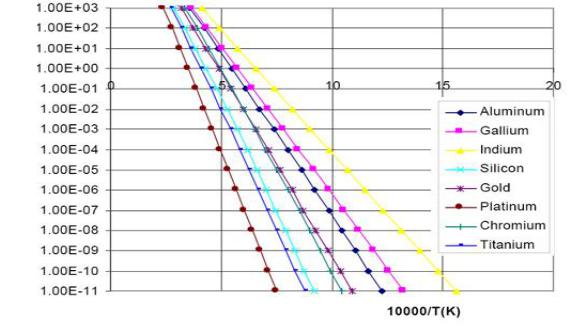
Давление пара, Торр
Обратная температура,
Рисунок 44 – Зависимость давления пара от температуры
Видно, что давление насыщенного пара является функцией, сильно зависимой от температуры.
Поэтому скорость испарения зависит от давления насыщенного пара. С практической точки зрения следует помнить, что некоторые материалы имеют давление насыщенного пара очень высокое при температуре ниже температуры плавления (хром, например).
Для того, чтобы обеспечить одинаковое давление насыщенного пара нужно испарить с поверхности одинаковое число атомов, т.е. получить одинаковый поток.
Чтобы обеспечить одинаковый поток атомов Al и атомов Cr, нужно расплавить алюминий, а хром можно испарить из твердого состояния.
Поэтому очень важным с точки зрения технологии является не температура плавления или кипения для испарения, а давление насыщенного пара. И оно же обеспечивает высокую скорость испарения (например, Cr, Al, Au).
Посмотрим, какие величины коэффициента испарения могут быть для разных веществ, т.е. для разных агрегатных состояний.
Жидкость С точки зрения технологии, нас интересует испарение из расплавов и для
большинства жидкостей (расплавов металлов) av 1. Монокристаллы
33
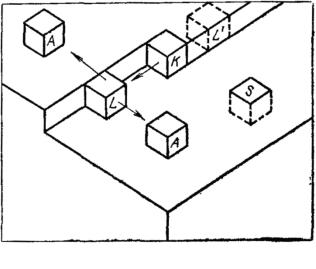
Испарение с поверхности монокристалла отличается от испарения с поверхности расплава и для объяснения этого отличия можно использовать модель, которая описывает испарение монокристаллов.
В данном случае легче всего испариться тому атому, у которого меньше связей (тот, который стоит одиночно).
Рассмотрим процесс обратный росту. Атом от ступеньки легирует в свободное место на поверхности (Рисунок 39, атом А) и затем происходит испарение с поверхности.
Понятно, что при росте пленки этот процесс имеет место быть, когда часть атомов покидает ступеньку, уходит на поверхность и испаряется.
Т.е. такие процессы каким-то образом уравновешиваются при определенных температурах подложки, что критически важно для получения эпитаксиальных пленок. Поэтому с точки зрения испарения мо-
нокристаллов является ориентация поверхности.
1)Для граней с малыми индексами расстояние между ступеньками превосходит среднее расстояние, проходимое атомом при диффузии. Для моноатомных паров аv → 1/3.
2)На гранях кристалла с высокими индексами на поверхности создается много ступенек, расстояния между которыми сравнимы со средним диффузионным расстоянием, которое проходят атомы, прежде чем они активируются
идесорбируются аv ≈ 1.
Все вышесказанное характерно для испарения одноатомной молекулы, а для некоторых твердых тел пар представляет собой не одноатомную молекулу на поверхности, поэтому в этом случае возможны изменения.
Поликристаллы.
Поликристаллические материалы (Ag, Сu, Be, Cd, Hg, Fe, Cr и Pt) в случае испарения одноатомного газа представляют собой нечто подобное монокристаллу с поверхностью с высокими индексами, поэтому в этом случае отрыв атома от кристалла упрощен и аv ≈ 1. Характер испарения поликристаллических твердых тел, которые испаряются в виде полимеров (Se, Те, As, Р, С) или
34
соединен ий, которые диссоциируют при испарении (AIN, BN, Аl2O3) определяется более сложной кинетикой. Например, для паров Те2 аv ≈ 1, а для P2 и P4
аv ≥10-7-10-6
В формуле Герца-Кнудсена a0=const и только p=f(T) а при испарении сложных соединений a0=f(T) и это также нужно учитывать.
Чистота поверхности критически важна – в большинстве случаев загрязнения и примеси ведут к уменьшению аv
Если на поверхности присутствуют примеси, то испарение обычно уменьшается и даже значительно.
Уравнение Герца-Кнудсена справедливо для испарения с поверхности. Один из методов испарения, сопровождающихся ростом эпитаксиальной пленки, является молекулярно-лучевая эпитаксия.
3.2.2. Молекулярно-лучевая эпитаксия.
Этот метод основан на процессе эффузии, т.е. истечением газа через отверстие в высоком вакууме, при этом отдельные молекулы проникают через отверстие без столкновений между собой.
Рисунок 46 – Иллюстрация для процесса эффузии
У нас есть некий объем – ячейка Кнудсена или эффузионная ячейка Кнудсена, в которой находится нагретое вещество. Это может быть расплав или соединение, в смысле твердая среда, нагретая до высоких температур.
Эффузия из изотермического объема с малым отверстием. Поскольку площадь, с которой происходит испарение внутри ячейки, >> A0, то внутри устанавливается равновесное давление р.
1) Диаметр отверстия <<λ(T,p).
35

2) Толщина стенки отверстия должна быть пренебрежимо малой с тем, чтобы частицы газа, покидающие ячейку, не рассеивались, не адсорбировались и не десорбировались.
При этих условиях поверхность испарения находится в равновесии с паром испаряемого вещества и отражения молекул пара не происходит, т, е, величина аv ≈ 1.
Тогда уравнение, описывающее испарение, имеет вид:
J |
0 |
= a |
|
p − p0 |
= |
|
p |
, |
(x37) |
|
|
|
|
||||||
|
|
|
2 mkT |
2 mkT |
|
|
|||
|
|
|
|
|
|
||||
Здесь p0 = 0 – внешнее давление столба газа, т.к. нанесение пленки происходит в высоком вакууме.
Вэтом случае расчет скорости испарения более простой: нет неопределенности с аv, нет обратного потока, поэтому такой метод часто используется для создания монокристаллических пленок.
Вэтом случае распыление или перенос материала выполняется в высоком вакууме, т.е. нет столкновений с атомами другого материала и вещество распространяется по прямой траектории от места выхода до точки осаждения.
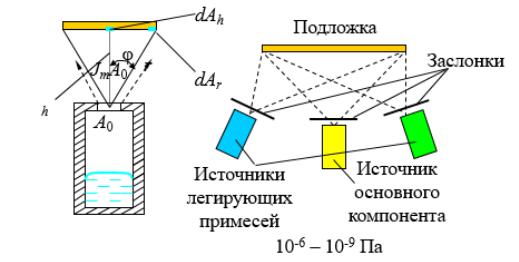
Обычная схема состоит из нескольких испарителей или нескольких ячеек Кнудсена для получения гетероструктур – монокристаллических структур, состоящих из атомов разного вещества.
Обычное давление, при котором происходит осаждение – 10-6-10-9 Па. Контроль поступления вещества осуществляется с помощью заслонок.
Скорость, с которой материал вытекает, описывается плотностью потока испаряемого вещества (х37) – сколько атомов вытекает с м2 поверхности за секунду.
Если мы умножим (х37) на массу атом, то получим плотность потока массы испаряемого вещества, т.е. сколько кг вытекает с м2 за секунду:
|
|
|
|
|
|
|
|
Jm = J0m = |
p m |
|
(х38) |
||||
|
|
|
|||||
2 kT |
|||||||
|
|
|
|
||||
Через молекулярную массу:
|
|
|
|
|
|
|
|
Jm = |
p M |
|
(х39) |
||||
|
|
|
|||||
2 RT |
|||||||
|
|
|
|
||||
Скорость испарения:
ности в единицу времени.
Um = Jm - какая толщина слоя испаряется с поверх-
Эффузионная ячейка Кнудсена
36
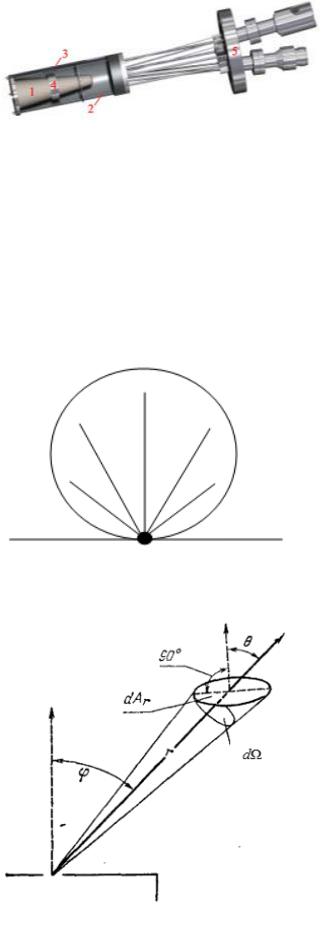
Эффузионная ячейка представляет из себя некий объем, который изолирован от внешней среды для того, чтобы не перегревался внешний материал, внутри которого помещено нагреваемое вещество.
Нагрев обычно осуществляется излучением резистивной нагреваемой нити, т.е. нить нагревается от высокой температуры и излучением
греет вещество.
Термопара необходима для контроля температуры нагреваемого материала. Защитная оболочка для предотвращения нагрева корпуса установки.
Всё это встраивается в камеру, вскрытие заслонки позволяет создавать поток вещества, который дальше переносится на подложку.
Важно отметить, что если мы построим распределение вещества по разным направлениям, то это распределение вещества описывается законом косинуса. Т.е. минимальная плотность потока наблюдается при направлении близком к нормали, когда cos=1, и не распространяется вещество в направлении касательной к поверхности, когда cos=0.
По аналогии с выражением, полученным в первой теме:
dM 0 |
( ) = Jст A0dt cos |
d |
(х40) |
|
|
||||
|
|
|
- масса вещества, которая выходит из ячейки Кнудсена.
Выделяем некоторый телесный угол dΩ, в котором можно наблюдать, сколько атомов движется в этом угле. cosφ – задает направление; А0 – площадь ячейки Кнудсена. Площадка dAr может
37

быть каким-то образом ориентирована относительно угла dΩ.
Если площадь ограничена телесным углом, равным dS, то, исходя из опре-
деления телесного угла: d = dSr2 - совокупность всех лучей, которые исходят
из данной точки и пересекают заданную поверхность.
Если увеличить площадь, то вещество размывается по большей площади, значит толщина в этой локальной области уменьшается, поэтому dAr связана с телесным углом Ω и углом ориентации этой поверхности следующим образом:
dAr = |
r2 d |
|
|
|
(х41) |
||
cos |
|||
|
|
Если мы теперь посмотрим, какая масса материала осаждается на этой площадке, то получим:
dM 0 |
( , ) |
= |
Jст A0dt |
cos cos |
|
||
dAr |
r |
2 |
(х42) |
||||
|
|
||||||
|
|
|
|
||||
- это масса вещества, которая испарилась из ячейки Кнудсена. Количество вещества, которое осаждается на противолежащую поверх-
ность, также зависит от положения этой поверхности относительно испарителя. Количество вещества, испаренного в пределах угла dΩ, осаждается на площади, величина которой возрастает с увеличением как расстояния до испарителя r, так и угла падения θ. Площадь элемента подложки для данных dΩ и
θравна.
Вбольшинстве случаев мы будем рассматривать не различную ориентацию подложки, а различную ориентацию ячейки Кнудсена.
Самая общая конфигурация – это несколько ячеек Кнудсена, которые расположены под определенным углом к подложке. Важно, что тогда плотность потока в разные точки, является величиной, которая является результатом двух углов: φ и θ, то есть в каждой точке будет разная плотность потока вещества, а значит, разная толщина пленки в разных точках.
38
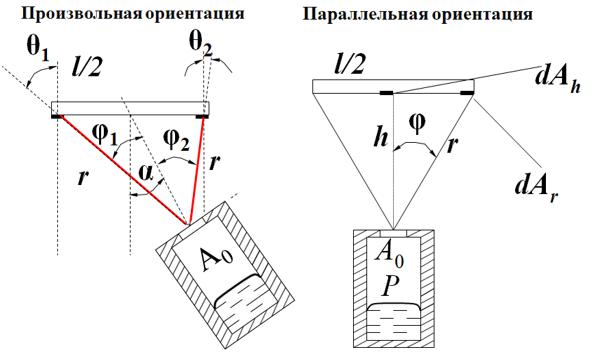
Рисунок 50 –
Самый простой случай – параллельная ориентация. В этом случае в каждой точке подложки φ=0. Тогда в каждой точке на подложке можно записать следующее уравнение:
|
Jm (r) = |
Jm A0 |
cos2 |
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
M0 = Jm A0t |
|
|
|
|
||||
L(l) = |
dM r |
|
= |
Jm (r )dAr t |
= |
|
M0 |
cos cos |
||
dAr |
|
|
dAr |
r2 |
||||||
|
|
|
|
|
|
|||||
- последнее выражение для нахождения толщины пленки в каждой точке на подложке.
Эффективным способом контроля роста пленок на месте является дифракция отраженных быстрых электронов.
39
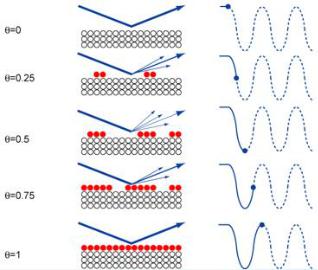
Пусть θ – доля покрытия равным слоем. При θ=0 подложка является чистой от дополнительных атомов. В этом случае все электроны, падающие на поверхность, отражаются, и интенсивность луча максимальна.
Допустим, что, после испарения из ячейки Кнудсена, у нас закрыта ¼ поверхности подложки (θ=0,25). За счет дифракции отраженных электронов под разными углами будет происходить уменьшение интенсив-
ности луча, падающего на детектор. В случае θ=0,25, сигнал уменьшится в 2 раза, а в случае θ=0,5. Далее, если степень покрытия атомами осажденного вещества увеличивается, то интенсивность начинает возрастать, и при θ=0,75 мы снова видим ½ сигнала. Как только формирование первого слоя завершено, интенсивность отраженных электронов снова будет максимальной.
При нанесении пленки важным является то, что подложки вращаются, так как при испарении из двух источников под разными углами получаются пленки, по-разному распределенные по поверхности. В точке кратчайшего расстояния будет максимальная толщина пленки. И, с точки зрения равномерности нанесения пленки, критически важно вращать подложку.
Другим важным моментом является температура нагрева. Она обычно очень высокая для того, чтобы позволить осажденным атомам диффундировать по поверхности. Но, если мы создаем структуру с четкими границами, например, примесь, то увеличение температуры приводит к тому, что примесь начинает расплываться. Нет возможности создать очень узкую зону высокой концентрации примеси.
3.2.3 Жидкофазная эпитаксия
Жидкофазную эпитаксию можно характеризовать как кристаллизацию слоя из растворов-расплавов на подложке определенной кристаллографической ориентации. При этом слой принимает ориентацию подложки.
Преимущества: относительно простое оборудование; большие скорости роста; большой выбор легирующих примесей; возможность регулирования отклонения состава кристаллов от стехиометрии при получении эпитаксиальных
40
