
тмиэт / Экзамен Тмеет / 3
.pdf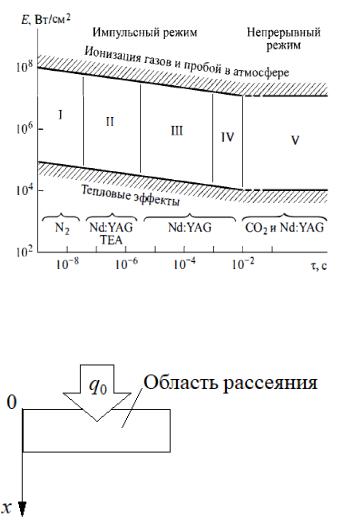
2.3. Взаимодействие фотонов с твёрдым телом
Энергия фотонов:
E0 = 0,1 0,4 эВ ( =10,6 0,3 мкм),
(x1)
E0 =10 150 эВ ( =100 8 нм),
Изменяя длину волны излучения λ, можно варьировать энергию, с которой фотоны попадают на поверхность твёрдого тела.
Физические эффекты на поверхности твердого тела будут зависеть от энергии. Например, если мы используем фотоны с энергией меньшей чем ширина запрещенной зоны полупроводника, то такие фотоны не будут поглощаться, так как энергии для перемещения электрона из валентной зоны в зону проводимости будет недостаточно. Если же мы будем использовать высоко-
энергетические фотоны, они будут |
|
||||||
активно поглощаться. |
|
|
|
||||
Лучше всего для этих целей ис- |
|
||||||
пользовать лазерное излучение, так |
|
||||||
как ни один другой вид излучения |
|
||||||
не позволяет получить столь высо- |
|
||||||
кую энергию на очень малой пло- |
|
||||||
щади |
поверхности. |
Существуют |
|
||||
разные типы лазеров и зачастую |
|
||||||
применяются два режима: непре- |
|
||||||
рывный и импульсный. |
|
|
|
||||
Сверху все режимы, представ- |
Рис. 2.3.1 l - испарение тонких пленок; II - скрай- |
||||||
ленные на рисунке 2.3, ограничены |
бирование, испарение пленок; III - сверление от- |
||||||
верстий; IV - точечная сварка V - глубокое про- |
|||||||
|
|
|
|
|
|
||
пробоем газа |
и |
его |
ионизацией, |
плавление |
|||
снизу же тело не успевает рассеи- |
|
||||||
вать по поверхности. |
|
|
|
||||
Лазерная абляция – метод уда- |
|
||||||
ления вещества с поверхности ла- |
|
||||||
зерным импульсом. |
|
|
|
||||
Представим |
мишень, |
на |
|
||||
поверхность |
которой |
направлен |
|
||||
поток |
фотонов |
с |
плотностью |
Рис. 2.3.2 Иллюстрация |
|||
|
|
|
|
|
|
||
мощности q0 (интенсивность с точки
зрения оптики). Фотоны поглощаются в некоторой области и эти поглощенные фотоны преобразуются в тепло.
Закон Бугера-Ламберта описывает изменение интенсивности фотонов внутри твердого тела:
q(x) = q0 (1 − R) exp(− x) , |
(x2) |
где q0 – первоначальная интенсивность (плотность потока мощности); exp(-αx) описывает поглощение фотонов; (1 - R) – коэффициент поглощения.
Для любого прозрачного диэлектрика должен выполняться закон сохранения энергии:
R +T + A =1, |
(x3) |
где R – коэффициент отражения; T – коэффициент прохождения; A – коэффициент поглощения.
Мы же будем рассматривать нагрев непрозрачных материалов, то есть T=0. В таком случае коэффициент поглощения:
A =1− R −T =1− R . |
(x4) |
2.3.1. Механизмы поглощения фотонов
Существует несколько механизмов поглощения:
1.Решеточное поглощение,
2.Собственное поглощение (для полупроводников),
3.Примесное поглощение (для полупроводников),
4.Поглощение свободными электронами.
1) Рассмотрим поглощение электронной подсистемой (свободными носителями).
Фотон передает свою энергию электрону. Электроны сталкиваются с кристаллической решёткой и передают избыточную энергию, поглощенную от электрического поля, атомам, т.е. возбуждают фотонные колебания, нагревая тем самым твердое тело (фотон → электрон → фонон).
Для того, чтобы количественно оценить, необходимо воспользоваться приближением: λ>> L, где L – длина свободного пробега электрона, λ – длина волны излучения.
То есть на одной длине волны электрон многократно сталкивается с другими атомами. Тогда можно записать, что плотность тока является функцией напряженности поля:
2

j(r, ) = ( )E(r, ) |
(x5) |
Из теории проводимости Друде 0 = ne2 - стационарная проводимость
m
(проводимость в поле нулевой частоты).
В случае высокочастотного поля, используя это выражение в совокупности с уравнениями Максвелла, можно записать зависимость для проводимости:
|
|
|
|
= |
|
0 |
, = 0 ( − i |
|
|
) |
, |
(x6) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
− i |
|
|
0 |
|
|
|
|
где τ – время, за которое электрон движется между соударениями. |
|
|||||||||||
Из уравнения (x6) следует две крайние ситуации: |
|
|||||||||||
1. Нормальный |
спин-эффект |
наблюдается |
для низких |
частот |
||||||||
( |
1; |
|
|
) . |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
В этом случае декремент затухания:
|
|
|
|
|
|
|
|
|
P = |
|
2 0 - по мощности, |
|
|
|
|
|
|
Me |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Me = |
2 0 - по амплитуде. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
, |
(x7) |
||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
Т.е. на глубине скин-слоя поле затухает в е раз, тогда решетка для элек- |
||||||||
трического поля: |
|
|
|
|
|
|||
|
|
|
E( y) = E ei y e− y , |
(x |
) |
|||
|
|
|
|
0 |
|
|
8 |
|
где E0 – амплитуда электрического поля на входе; β – постоянная распространения; iβy – характеризует фазу волны; e− y - показывает, во сколько раз поле при прохождении расстояния y.
Если рассчитать действительную часть этого выражения, то найдем распределение поля в пространстве:
Re(E( y)) = Re(E ei y e− y ) = e− y cos( y) |
(x |
) |
0 |
9 |
|
Иллюстрацией к уравнению (x9) служит рисунок 2.3.1, представленный ниже:
3
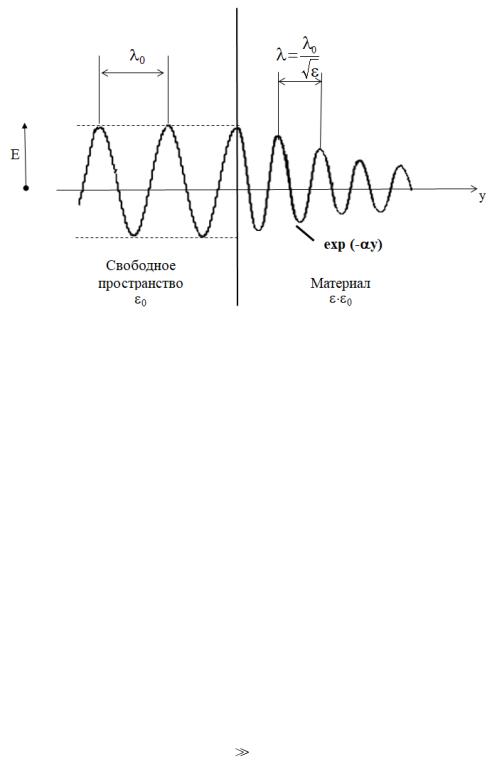
Рис. 2.3.1 – Распределение поля в пространстве
Если мы будем рассматривать свободное пространство и материал с ка- кой-то проводимостью, в котором выполняется нормальный скин-эффект, то на входе в свободное пространство гармоническая функция (cos), амплитуда которой не изменяется, а внутри материала e− y cos( y) и амплитуда этого косинуса будет уменьшаться.
Металлы в этом случае характеризуются большим коэффициентом отражения, так как, если мы возбудили колебания электронов, то эти электроны снова возбуждают электрическое поле.
В таблице ниже представлены значения коэффициентов отражения R для некоторых металлов при λ=1,06 мкм:
Таблица 1 – Значения коэффициентов отражения для некоторых металлов при λ=1,06 мкм
Металл |
Cu |
Al |
Ni |
|
Сталь |
Ag |
Cr |
W |
Pt |
|
|
|
|
|
|
|
|
|
|
R |
0,90 |
0,75 |
0,72 |
|
0,58 |
0,96 |
0,57 |
0,62 |
0,72 |
|
|
|
|
|
|
|
|
|
|
2. Высокочастотный случай ( |
1) |
|
|
|
|
||||
Металлы на очень высоких частотах становятся прозрачными для электромагнитного излучения. Частота, при которой выполняется это условие, называется плазменной частотой. В этом случае ɛ можно записать в виде:
|
|
|
2 |
|
|
|
(1− |
|
p |
) |
(x10) |
|
2 |
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
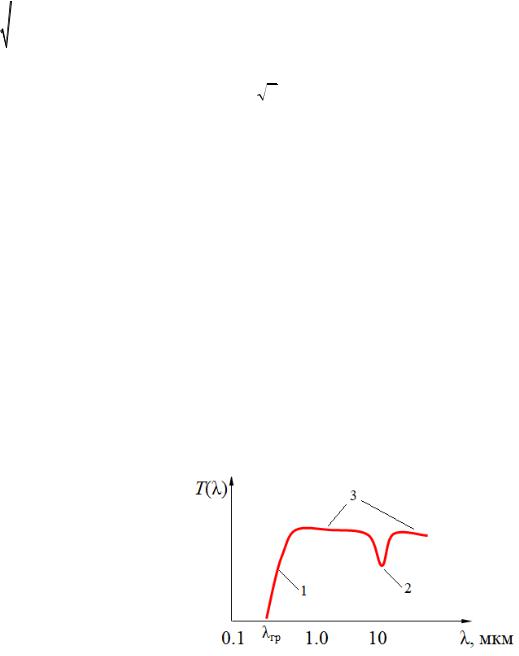
Плазменная частота задаёт нам граничную длину волны:
|
|
|
|
гр |
= |
2 с |
(x11) |
|
|
|
|
гр |
|||||
|
|
|
|
|
|
|
||
где гр = р = |
ne2 |
|
. Т.е. при частоте излучения большей, чем плазменная ча- |
|||||
0m |
||||||||
|
|
|
|
|
|
|
||
стота, материал становится прозрачным для электромагнитного излучения. Связь показателя преломления n и ɛ: n = 
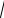
Тогда, если р , то 0 и n мнимая, значит происходит затухание. Если р , то 0 и n вещественная, следовательно, металл неотличим от диэлектрика.
3. Пограничный случай – аномальный скин-эффект (λ < l)
Если же расстояние, на котором электрон движется свободно, становится больше, чем толщина скин-слоя на высоких частотах, тогда получается, что поле изменяется на длине свободного пробега и полученные ранее формулы не работают – необходимо более сложное решение выражения (5).
Т.е. при увеличении частоты поля или длины свободного пробега (при уменьшении температуры металла) глубина проникновения уменьшается ( l) . Тогда коэффициент прохождения можно изобразить следующим образом:
Область 1 – аномального |
|
|
спин-эффекта – ниже граничной |
|
|
длины волны металл становится |
|
|
прозрачным для электромагнит- |
|
|
ного излучения ( р ). |
|
|
Область 2 – резонансная ча- |
|
|
стота поглощения решетки. |
|
|
Область 3 – область нор- |
Рис. 2.3.1.2 – Зависимость коэффициента |
|
мального скин-эффекта. |
||
прохождения от длины волны |
В кристаллической решетке есть частоты собственных колебаний, которые могут эффективно поглощать энергию внешнего оптического излучения
– такой механизм называется решеточное поглощение. Оно наблюдается при взаимодействии излучения непосредственно с атомами кристаллической решетки. При этом электронная подсистема остается незадействованной – взаимодействие фотона с фононом (т.е. оно квантовано).
5
Здесь возникают дополнительные трудности:
1. Проводимость зависит от температуры: 0 = ne2 .
m
Сопротивление металлов растет с ростом температуры, т.к. атомы начинают сильнее колебаться и увеличивается вероятность столкновения электрона с атомом и передачи энергии.
Для описания этой зависимости используется зависимость времени от температуры:
(T ) = |
|
, |
(x12) |
|
T |
|
|
где θ – температура Дебая (все частоты возбуждены), τθ – время релаксации при температуре Дебая.
Соответственно, с увеличением температуры, уменьшается проводимость 0 , а сопротивление увеличивается и коэффициент поглощения растет.
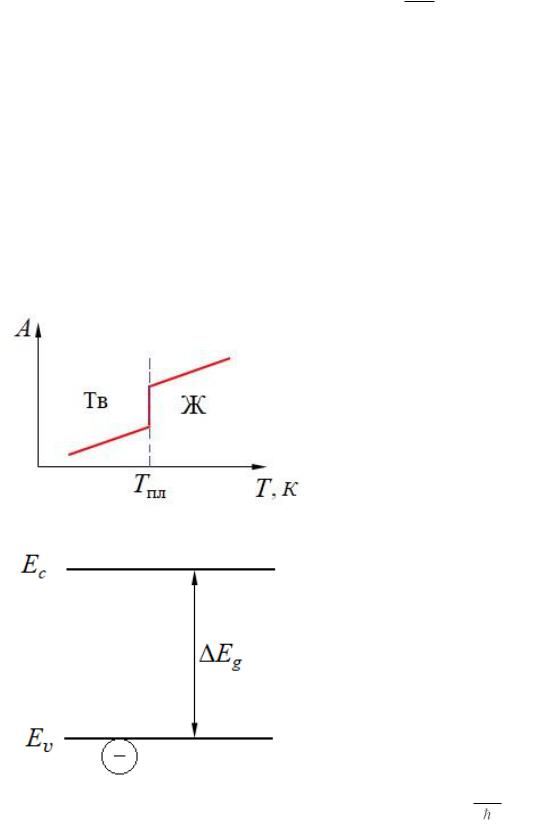
При этом в точке фазового перехода из твердого состояния в жидкое состояние, происходит скачкообразное увеличение коэффициента поглощения, т.к. пропадает дальний порядок (в жидкости остается только ближний) (Рис. 2.3.1.3)
Рис. 2 – Иллюстрация
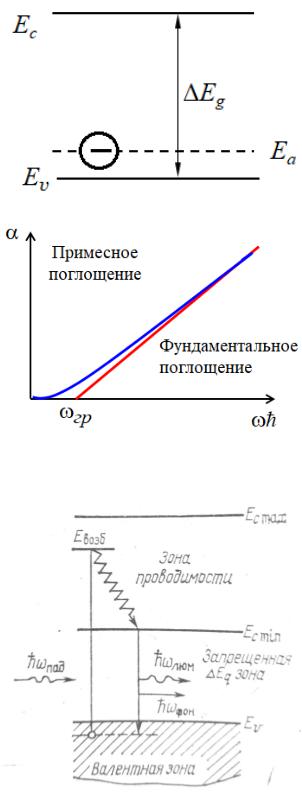
2. Фундаментальное или основное поглощение.
Фотон поглощается атомом и электрон из валентной зоны переходит в зону проводимости. Соответственно, для такого поведения есть некоторая пороговая частота и, если энергия фотона ниже, то поглощения не произойдет:
гр = Eg .
Рис.3 - Иллюстрация
6
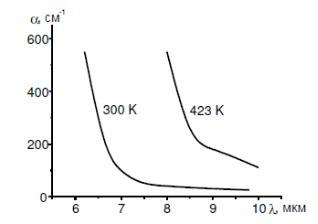
3.Примесное поглощение.
Данное поглощение отличается тем, что переход осуществляется на уровнях примеси, которые могут быть расположены на разной глубине запрещенной зоны (Рис.4).
В таком случае для фундаментального поглощения характерно наличие некоторой частоты гр , ниже которой
поглощения не происходит. А для примесного поглощения зависимость является размытой, так как существует много дополнительных уровней, с которых может происходить переход. (Рис.5)
Как же энергия передается кристаллической решетке при фундаментальном и примесном поглощении?
Здесь существует несколько механизмов: 1. Если энергия фотона чуть энер-
гии запрещенной зоны Eg , то элек-
троны забрасываются на некоторый уровень, который со временем релаксирует на дно зоны проводимости, что
сопровождается передачей |
энергии |
кристаллической решетки Евозб |
− ЕC min . |
Рис. 4
Рис. 5
2. Сам переход может происходить как с излучением – энергия отобрана фотоном, так и безизлучательно, т.е. возбуждается фонон, при этом вся
энергия поглощенного фотона перехо- Рис. 6 – Механизмы перехода дит в тепло (Рис.6).
При очень высоких температурах доминирует безизлучательный переход. Также для полупроводников характерно то, что при очень высоких интенсивностях, когда в зоне проводимости накапливается большое количество
7
электронов, начинает доминировать поглощение свободными электронами – металлизация полупроводника.
Рис. 7 -
нии.
Заметим, что декремент затухания также зависит от температуры (Рис.7): ширина запрещенной зоны зависит от температуры и с ростом температуры уменьшается:
Eg (T ) = Eg 0 − T , |
(x13) |
где δ – коэффициент, зависящий от материала.
Такое поведение связано с линейным расширением тел при нагрева-
Уменьшение запрещенной зоны приводит к тому, что, с ростом температуры, кривая смещается в область более низких частот, поэтому при повышении температуры поглощение возрастает.
Нагрев диэлектриков связан с такими параметрами как:
1.Поверхностное загрязнение, из-за которого металл может проплавляться локально.
2.Поглощение на примесях и дефектах.
3.Многофотонное поглощение – нелинейный процесс, который наиболее эффективен при больших интенсивностях, т.е. если энергии одного фотона может не хватать для преодоления запрещенной зоны, то электрон может преодолеть запрещенную зону при сложении энергий двух фотонов.
4.Нелинейный эффект Керра и самофокусировка лазерного излуче-
ния (n = n0 + n2 I )
5.Вынужденное рассеяние Мандельштама-Бриллюэна (переменное электрическое поле световой волны в результате электрострикции вызывает переменную деформацию в веществе, возбуждая таким образом акустические волны, которые рассеиваются на поверхности или дефектах, преобразуясь в тепловую энергию).
8
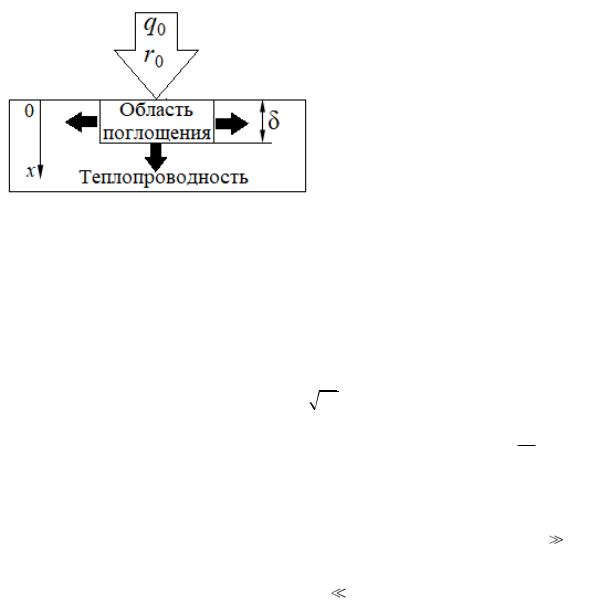
2.3.2. Нагрев объемного материала
Пусть на поверхность металла направлен лазерный поток с плотностью мощности q0 и радиусом r0. Фотоны поглощаются в очень узкой области δ. При этом часть энергии уходит по поверхности и часть энергии уходит вглубь.
Плотность мощности:
Рис. 8 - |
q0 |
= |
|
E |
= |
|
P |
|
, |
(x14) |
|
r2 |
r |
2 |
|||||||
|
|
|
0 |
|
0 |
|
|
|||
где Е – энергия лазерного импульса; τ – длительность импульса. Можно выделить три характерных времени:
1.Время нагрева электронного газа в металлах: =10−11 10−13 с .
2.Время релаксации и передачи избыточной энергии решетке: =10−10 10−11 с
3.По истечении времени (t 10−10 с) размер прогретой области начинает увели-
чиваться пропорционально величине 
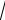 at , характеризующей размер разогре-
at , характеризующей размер разогре-
м2
той области к моменту времени t; а – температуропроводность .
с
Здесь мы должны решать уравнение теплопроводности, и для того, чтобы его решение упростить, рассмотрим на металле область, в которой происходит поглощение 10−8 м , в то же время радиус пучка r0 ≈ 10-4 м, т.е. r0 δ. Если мы решаем такую задачу, то мы можем считать, что тепло по сторонам не расходится, т.к. площадь этих границ: 2πr0δ r02 (площадь нижней границы).
В этом случае мы можем записать одномерное уравнение Фурье с нулевой правой частью:
T (x, t) |
|
2T (x, t) |
|
|
|
м2 |
|
|
|
|
− a |
|
|
= 0, |
a |
|
|
, |
|
t |
t |
2 |
с |
||||||
|
|
|
|
|
|
|
|||
|
|
Вт |
|
(x15) |
|
|
|
|
|
||
|
|||||
|
|
м с |
|
||
Нулевая правая часть говорит о том, что источник тепла – поверхностный, и область поглощения δ пренебрежимо мала.
Для решения ДУ нужны начальные и граничные условия:
|
|
|
|
|
|
|
T ( , t) = 0, температура на бесконечном удалении равна нулю |
||||||
|
T (0, t) |
|
|
|
|
. |
|
= (1 |
− R)q0 |
− |
для r r0 − |
||
− |
x |
поток тепла через поверхностную границу |
||||
|
|
|
|
|
|
|
Начальные условия:
9
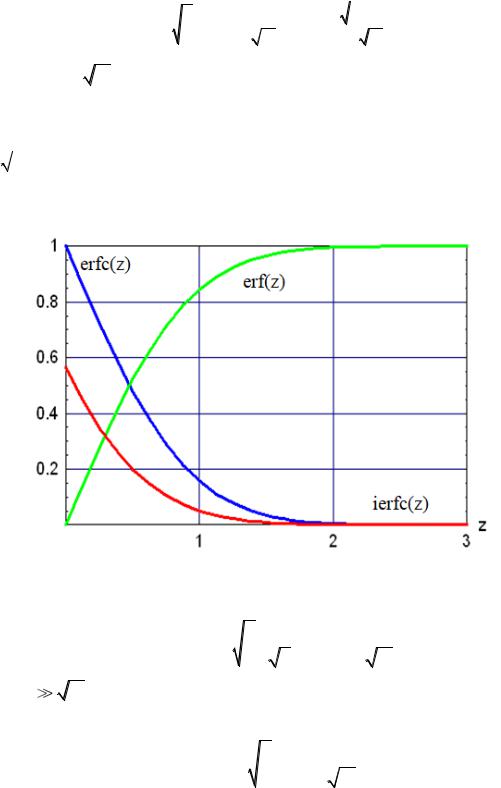
T (x, 0) = 0 - температура по всей координате х в нулевой момент времени равна нулю.
1. Тогда решение этого уравнения при t≤τ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + r2 |
|
||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
x |
|
|||||||||
|
|
|
|
|
|
T (x,t) = T |
|
ierfc |
−ierfc |
|
0 |
|
(x16) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
2 at |
|
|
||||||||
|
|
|
|
|
|
|
|
2 at |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2q0 (1− R) |
at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Tm = |
, ierf(z)= |
|
erfc(dx) |
|
− интеграл от доп.функции ошибок, |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
erf(z)= |
|
2 |
|
z e−x2 dx |
− функция ошибок, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
erfc(z) =1− erf (z) − дополнительная функция ошибок.
Рис. 9
Если подставить x = 0, то найдем температуру поверхности:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
r |
|
|
|
||||||||
|
|
Tпов = T (0,t) = Tm |
|
|
|
|
|
|
|
|
− ierfc |
|
|
|
0 |
|
|
(x17) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
at |
|
||||||||||
Если r0 |
at , то боковым отводом тела можно пренебречь, считая, что |
|||||||||||||||||||||||
поверхность облучается равномерно. В таком случае |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
t |
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
|
|
T (x,t) Tm |
|
|
|
|
|
ierfc |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
at |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
10
