- •2. Взаимодействие концентрированных потоков энергии с твердым телом
- •2.1. Взаимодействие ускоренных электронов с твердым телом. Вторичные эффекты. Система координат.
- •2.1.1. Торможение электрона
- •2.1.2. Траекторный и проекционный пробеги
- •2.1.3. Диффузионная модель
- •2.1.4. Электронно-лучевой нагрев
- •2.1.5. Применение электронного пучка.
2. Взаимодействие концентрированных потоков энергии с твердым телом
2.1. Взаимодействие ускоренных электронов с твердым телом. Вторичные эффекты. Система координат.
Концентрированные
потоки энергии (КПЭ) создают с помощью
заряженных частиц, ускоренных в
электрическом поле, или фотонов,
генерируемых, например, лазером. При
взаимодействии КПЭ с твердым телом
происходит отражение и поглощение
потока
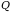 :
:
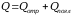
 Отражённую
энергию уносят во внешнюю среду частицы
и фотоны.
Отражённую
энергию уносят во внешнюю среду частицы
и фотоны.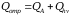 .
Появление во внешней среде частиц и
фотонов с суммарными энергиями
.
Появление во внешней среде частиц и
фотонов с суммарными энергиями
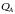 и
и
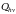 соответственно, может быть обусловлено
как отражением части па-дающего потока,
так и эмиссией из твердого тела под
воздействием КПЭ.
соответственно, может быть обусловлено
как отражением части па-дающего потока,
так и эмиссией из твердого тела под
воздействием КПЭ.
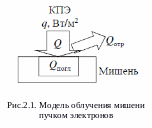
Поглощённая энергия расходуется на возбуждение и ионизацию атомов, генерацию точечных дефектов и нагрев мишени. Эти процессы могут инициировать в мишени фазовые переходы (плавление, кипение, перестройку кристаллической структуры и т.д.) и химические реакции. Отметим особенности нагрева материала мишени под воздействием КПЭ. Можно выделить два типа процессов:
1)
при плотности потока мощности
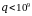 Вт/м2
скорость тепловыделения меньше скорости
отвода тепла из зоны нагрева за счет
теплопроводности. Это так называемый,
мягкий
режим,
при котором до 60 % мощности отводится
из зоны нагрева, а на плавление и испарение
расходуется примерно 35 % и 5 % соответственно.
Вт/м2
скорость тепловыделения меньше скорости
отвода тепла из зоны нагрева за счет
теплопроводности. Это так называемый,
мягкий
режим,
при котором до 60 % мощности отводится
из зоны нагрева, а на плавление и испарение
расходуется примерно 35 % и 5 % соответственно.
2)
при
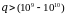 Вт/м2
скорость тепловыделения становиться
сравнимой со скоростью теплоотвода,
или превышает её. Это жесткий
режим.
Он характерен для электронного и
лазерного пучков. При такой высокой
плотности мощности большая её часть
расходуется на разогрев зоны тепловыделения
и выброс расплава из неё. Возникает
эффект кинжального проплавления, при
котором диаметр возникающего канала
существенно меньше его длины.
Вт/м2
скорость тепловыделения становиться
сравнимой со скоростью теплоотвода,
или превышает её. Это жесткий
режим.
Он характерен для электронного и
лазерного пучков. При такой высокой
плотности мощности большая её часть
расходуется на разогрев зоны тепловыделения
и выброс расплава из неё. Возникает
эффект кинжального проплавления, при
котором диаметр возникающего канала
существенно меньше его длины.
Следует иметь в виду, что на пути к поверхности объекта первичные электроны могут терять энергию и изменять направление движения. Изменение направления движения может происходить за счет электронно-оптических систем, которые обеспечивают фокусировку потока электронов с помощью системы магнитных и электрических линз. Число актов рассеяния на частицах определенного сорта пропорционально концентрации этих частиц, сечению соответствующего процесса и протяженности электронного потока. Поддержание высокого вакуума значительно снижает число актов рассеяния и ионизации. Однако в области все равно присутствуют остаточные газы и поток атомов с поверхности мишени, чья ионизация будет происходить, тем самым уменьшая энергию потока
Рассмотрим процессы, происходящие непосредственно в твердом теле и на его поверхности. При прохождении границы раздела вакуум - твердое тело первичные электроны ускоряются в поле сил поверхностного потенциального барьера и продолжают движение в веществе с возросшей кинетической энергией. На своем пути они испытывают многочисленные акты взаимодействия с атомами твердого тела, которые можно разделить на два основных класса - упругие и неупругие.
Под упругими понимают взаимодействие, при котором участвующие в нем частицы обмениваются кинетической энергией, а их внутренняя энергия не изменяется. При таком типе соударения происходит перераспределение кинетической энергии и возбуждение фотонных колебаний. Если при упругом соударении электрон не может передать атому энергию, достаточную для возбуждения фонона, то после рассеяния изменится только направление его движения, а энергия останется неизменной.
Неупругими называют такие взаимодействия, в которых кинетическая энергия переходит в изменение внутренней энергии (ионизацию внутренних энергетических уровней). Они обеспечивают торможение и разложение химических связей. Нагрев обеспечивает испарение (сублимацию).
Возбуждение фотонных колебаний приводит к нагреву мишени. Ионизация приводит к появлению вторичной фотонной эмиссии неупруго и упруго отраженных электронов. Если внутри тела происходит ионизация и возбуждение, то происходить химические изменения за счет перестройки связей.
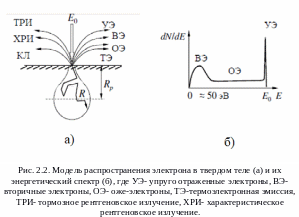
Пусть электроны с энергией Е0, которые сфокусированы на поверхности мишени, проникая в мишень, распространяются по ломанным траекториям длинной R, в узлах которых происходит упругое рассеяние. Тогда Rp – нормаль среднего траекторного пробега на ось вглубь материала- проекционный пробег.


Рассмотрим энергетический спектр данных электронов. Как видно по рисунку 2.2 б максимальной энергией обладают упруго отраженные электроны (УЭ), пик ВЭ соответствует вторичным электронам, выбитым с орбиталей атомов. Между пиками расположены оже-электроны- это электроны, выбитые с внутренней оболочки атома. Энергии больше 50 эВ характерны для неупруго рассеянных электронов и оже-электронов.
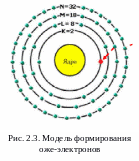 Рассмотрим
подробнее оже-эффект. В
результате
неупругого рассеяния электрон
выбивается
с одной из внутренних оболочек атома,
а электроны
с
верхних уровней занимают освободившееся
место. Если выделяемая в результате
энергия Ek-EM
предаётся электрону, расположенному
на внешнем уровне, то такой электрон
будет
в состоянии покинуть мишень.
Рассмотрим
подробнее оже-эффект. В
результате
неупругого рассеяния электрон
выбивается
с одной из внутренних оболочек атома,
а электроны
с
верхних уровней занимают освободившееся
место. Если выделяемая в результате
энергия Ek-EM
предаётся электрону, расположенному
на внешнем уровне, то такой электрон
будет
в состоянии покинуть мишень.
ТРИ излучается, когда электроны, распространяясь вблизи ядра атома резко изменяют свою траекторию, что приводит к изменению их энергии. В случае ХРИ первичные электроны выбивают электроны с внутренних орбиталей с образованием вакансий, в которую переходят электроны с внешних уровней, излучая квант ХРИ. Катодолюминесценция возникает вследствие бомбардировки ионами катода (мишени).
Рассмотрим системы координат, применяемые для изучения процессов взаимодействия электронов с твердым телом.

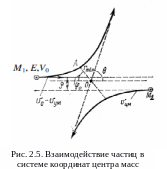 В
лабораторной
системе координат
электроны с массой М1
и скоростью υ0
налетают на частицу с массой М2.
Здесь ρ- прицельный параметр-
это
расстояние, на котором М1
прошла бы мимо M2, если бы взаимодействие
между ними отсутствовало. В модели
жестких сфер частица распространялась
бы по пунктирной траектории, в нашей же
модели между частицами действуют
кулоновские силы, которые отталкивают
их, что приводит к упругому взаимодействию.
Однако в такой системе координат очень
сложно описывать взаимодействие ионов
с электронами. Чтобы этого избежать
рассмотрим другую систему.
В
лабораторной
системе координат
электроны с массой М1
и скоростью υ0
налетают на частицу с массой М2.
Здесь ρ- прицельный параметр-
это
расстояние, на котором М1
прошла бы мимо M2, если бы взаимодействие
между ними отсутствовало. В модели
жестких сфер частица распространялась
бы по пунктирной траектории, в нашей же
модели между частицами действуют
кулоновские силы, которые отталкивают
их, что приводит к упругому взаимодействию.
Однако в такой системе координат очень
сложно описывать взаимодействие ионов
с электронами. Чтобы этого избежать
рассмотрим другую систему.
В системе координат центра масс движутся не частицы, а их центр масс. Благодаря этому можно видеть, как разлетаются частицы. Получается, что частица М1 движется со скоростью υ0-υцм, а частица М2 ос скоростью υцм. В этом случае задача рассеяния описывается одним углом. Минимальное расстояние rmin, на которое сближаются частицы, определяется из условия, когда кинетическая энергия, с которой распространяется один заряд, будет равна его потенциальной энергии. Приведем основные соотношения для данной системы координат:
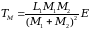 -
максимальная
кинетическая энергия, передаваемая
частице при столкновении, при этом ρ=0.
-
максимальная
кинетическая энергия, передаваемая
частице при столкновении, при этом ρ=0.
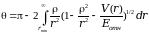 -
угол,
на который будет происходить рассеяние,
где
-
угол,
на который будет происходить рассеяние,
где
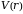 -
потенциальная энергия взаимодействия
двух частиц,
-
потенциальная энергия взаимодействия
двух частиц,
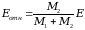 -
энергия движущейся частицы в данный
системе координат. Не трудно понять,
что если
-
энергия движущейся частицы в данный
системе координат. Не трудно понять,
что если
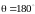 ,
то
это лобовое столкновение, а при
,
то
это лобовое столкновение, а при
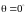 удара
не происходит, следовательно, энергия
не передается. Также получается, что
из-за угла
удара
не происходит, следовательно, энергия
не передается. Также получается, что
из-за угла
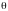 передаваемая энергия будет меньше чем
TM
и
принимает значение равное:
передаваемая энергия будет меньше чем
TM
и
принимает значение равное:
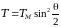
Перейти из системы координат центра масс в лабораторную можно с помощью следующих соотношений:
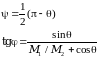
Если М1 << М2, то это рассеяние электрона на атоме, тогда:
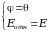
Если М1 = М2, то это рассеяние двух одинаковых частиц, тогда:
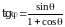
Мы рассмотрели столкновение лишь двух частиц, хотя в реальности сталкивают пучки, состоящие из большого число частиц, рассеяние в которых, к тому же, происходит под разными углами. Поэтому введем понятие дифференциального сечения рассеяния- вероятность рассеивания частиц в выбранном направлении:
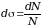
,
где dN-число
частиц, рассеивающихся на углы в диапазоне
от
до
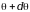 .
.
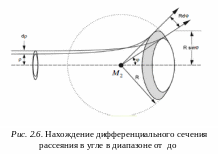 Для
случая, представленного на рисунке 2.6,
нужно найти число частиц, рассеянных в
сторону детектора (закрашенной области)
к общему числу частиц. В лабораторной
системе координат можно ввести величину
Для
случая, представленного на рисунке 2.6,
нужно найти число частиц, рассеянных в
сторону детектора (закрашенной области)
к общему числу частиц. В лабораторной
системе координат можно ввести величину ,где
,где
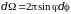 - телесный угол, характеризующую какая
доля частиц попадает внутрь детектора.
Так как дифференциальное сечение можно
представить как
- телесный угол, характеризующую какая
доля частиц попадает внутрь детектора.
Так как дифференциальное сечение можно
представить как
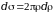 ,
мы можем выразить число частиц в рамках
телесного угла к общему числу частиц
как:
,
мы можем выразить число частиц в рамках
телесного угла к общему числу частиц
как:
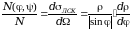
При взаимодействии двух заряженных частиц между ними возникает сила, описать которую можно при помощи закона Кулона:
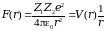 ,
,
где V(r)- потенциальная энергия взаимодействия. Чтобы найти связь между ρ и подставим полученную формулу в уравнение для угла рассеяния. Получившееся выражение справедливо только для упругого взаимодействия и показывает вероятность рассеяния под различными углами. Оно также называется формулой Резерфорда:
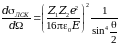
Для электронов, рассеивающихся на атомах, выражение принимает вид: