Схемота / DgCXT_Labs__1_v2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ЭПУ

отчет

по лабораторной работе №1

по дисциплине «Цифровая схемотехника»

Тема: ОЗНАКОМЛЕНИЕ С ЛАБОРАТОРНЫМ СТЕНДОМ И ИССЛЕДОВАНИЕ ПРОСТЕЙШИХ КОМБИНАТОРНЫХ ЛОГИЧЕСКИХ СХЕМ

		Яковенко Е.В.
		Шапошников В.А.
Студенты гр. 7201		Шурыгин А.С.
Преподаватель		Аристов С.А.

Санкт-Петербург

2020

Цель работы.

Ознакомиться с лабораторным стендом, изучить логические элементы и использование их в простейших комбинаторных логических схемах.

Основные теоретические положения.

Цифровая схемотехника на уровне составления электрических принципиальных схем оперирует не электрическими физическими величинами, а логическими уровнями.

Сама суть цифрового сигнала следует из ограничений, которые на него изначально накладываются. Одна цепь несет информацию бинарного вида – «истина/ложь», «да/нет», «готов/не готов», «открыто/закрыто», «o.k./ошибка». Если ряд цифровых сигналов объединить и условно пронумеровать, то полученная шина позволит записывать и передавать двоичные числа. Поскольку сигнал в одной цепи принимает лишь два значения (0,1), то количество комбинаций уровней сигналов в шине из двух цепей составит 4 (00, 01, 10, 11), из трех – восемь (000…111), и т.д.

ЛЭ сами по себе могут быть как частью сложных схемотехнических блоков, так и выполнять самостоятельные функции.

Ввиду большой гибкости при составлении сложных логических схем, имеющих много входов и выходов, особую популярность приобрели универсальные ЛЭ в интегральном исполнении. От простейших И/ИЛИ они отличаются тем, что результат сложения/умножения дополнительно инвертируется.

Имея лишь универсальные ЛЭ одного типа, можно построить как любые ЛЭ другого типа, так и вообще, теоретически, любое цифровое устройство. В частности, согласно законам Де Моргана,

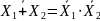и

Обработка результатов эксперимента.

1. Исследование ЛЭ типа 2И-НЕ:

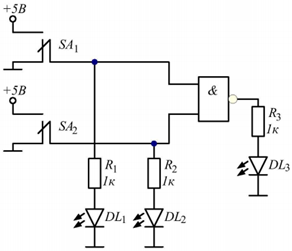
Рис.1 Схема для исследования таблиц истинности ЛЭ 2И-НЕ

Табл.1 Таблица истинности ЛЭ типа 2И-НЕ

х1	х2	y
0	0	1
0	1	1
1	0	1
1	1	0

Можно сказать, что данный ЛЭ инверсированный ЛЭ И.

2. Исследование ЛЭ типа 2ИЛИ-НЕ:

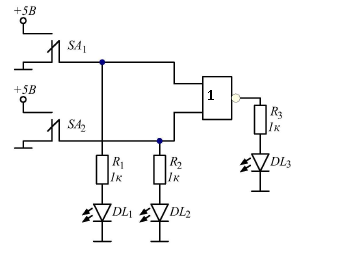
Рис. 2 Схема для исследования таблиц истинности ЛЭ 2ИЛИ-НЕ

Табл.2 Таблица истинности ЛЭ типа 2ИЛИ-НЕ

х1	х2	y
0	0	1
0	1	0
1	0	0
1	1	0

Можно сказать, что данный ЛЭ- инверсированный ЛЭ ИЛИ.

3. Исследование неизвестного ЛЭ:

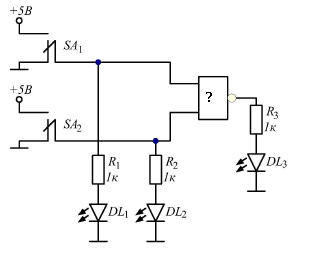
Рис. 3 Схема для исследования таблиц истинности неизвестного ЛЭ

Табл.3 Полученная таблица истинности неизвестного ЛЭ

х1	х2	y
0	0	0
0	1	1
1	0	1
1	1	0

Данная таблица истинности соответствует ЛЭ- исключающее ИЛИ.

4. Исследование ЛЭ типа 2И-НЕ, реализующего функцию ИЛИ:

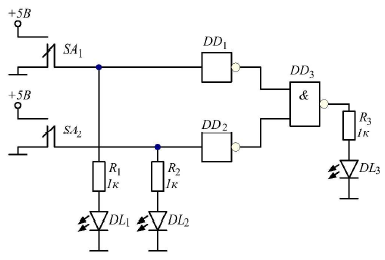
Рис.4 Реализация функции ИЛИ на ЛЭ типа 2И-НЕ

Табл.4 Таблица истинности для функции ИЛИ на ЛЭ типа 2И-НЕ

х1	х2	y
0	0	0
0	1	1
1	0	1
1	1	1

Получили совпадение таблицы истинности исследуемой схемы и ЛЭ И

5. Исследование одноразрядного сумматора:

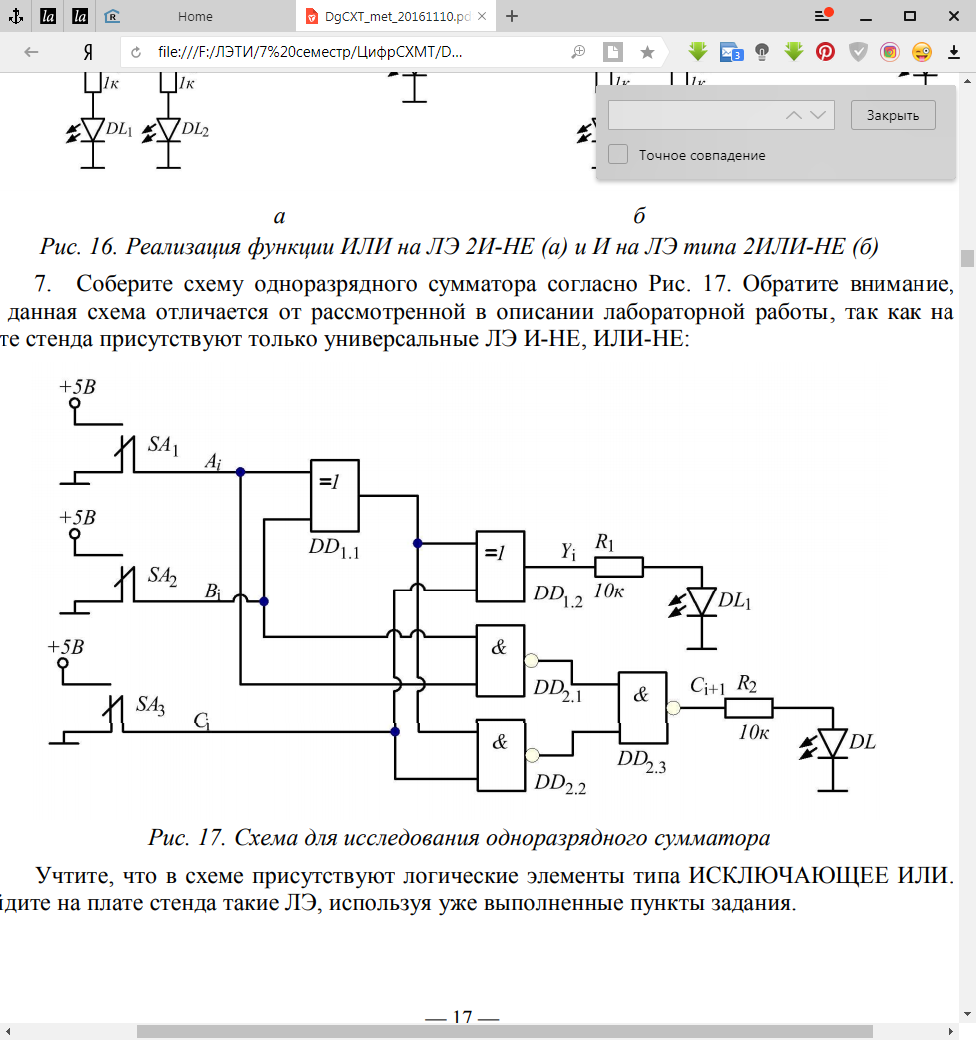
Рис.5 Схема для исследования одноразрядного сумматора

Табл.5 Таблица истинности для одноразрядного сумматора

Выражение	Результат (двоичное число)	Результат (десятичное число)
0+0+0	0	0
0+0+1	01	1
0+1+0	01	1
0+1+1	10	2
1+0+0	01	1
1+0+1	10	2
1+1+0	10	2
1+1+1	11	3

Данная схема демонстрирует работу сумматора и при сумме от двух высоких логических уровней происходит перенос в старший разряд.

6. Исследование дешифратора «2 в 4» :

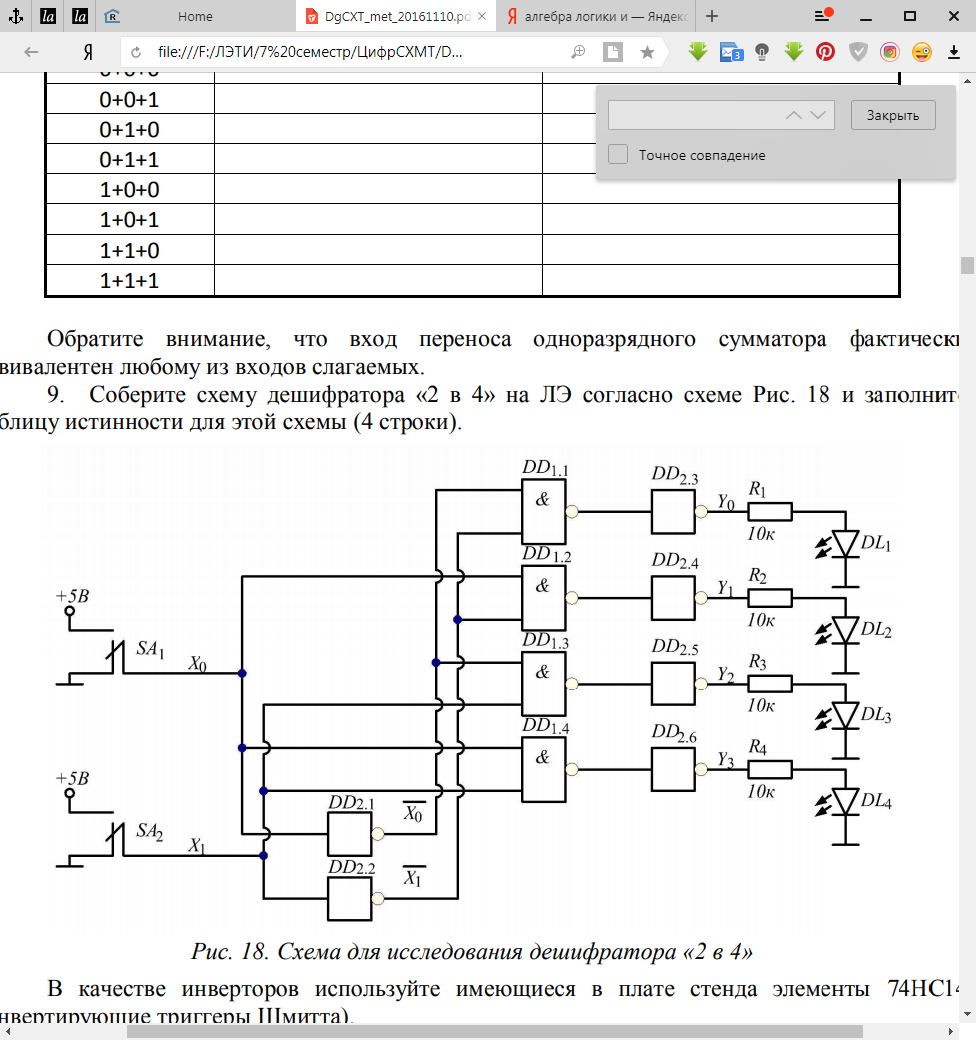
Рис.6 Схема для исследования дешифратора «2 в 4»

Табл.6 Таблица истинности полученная для дешифратора «2 в 4»

х1	х2	y
0	0	1000
0	1	0100
1	0	0010
1	1	0001

Вывод:

В данной лабораторной работе были исследованы схемы с ЛЭ «И-НЕ», «ИЛИ-НЕ», «Исключающее ИЛИ», схема для исследования реализации функции «ИЛИ» на ЛЭ типа «2И-НЕ», одноразрядный сумматор, а также дешифратор. Полученные результаты полностью совпадают с теорией.

Также был определен заранее неизвестный ЛЭ. По экспериментальным данным можем утверждать, что ЛЭ- это «Исключающее ИЛИ».

Протокол:

Бригада №2