
МИНОБРНАУКИ РОССИИ
Государственное образовательное учреждение
высшего профессионального образования
Санкт-Петербургский государственный электротехнический университет
«ЛЭТИ» им. В.И. Ульянова ( Ленина)
ФАКУЛЬТЕТ ЭЛЕКТРОНИКИ (ФЭЛ)
КАФЕДРА Радиотехнической электроники
КУРСОВАЯ РАБОТА (ПРОЕКТ)
По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ
На тему: Разработка модуля программы анализа электронного прибора
(указывается обобщенная тема)
Вариант № 7
Выполнил |
|
|
Оценка |
|
студент гр. № |
5201 |
|
Проверил |
Синев А. Е. |
|
Вакула Н.В. |
|
|
(ФИО) |
|
(ФИО) |
|
Дата |
|
САНКТ-ПЕТЕРБУРГ
2019 г.
Задание на курсовую работу
По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ
.
Название курсовой работы: |
Модуль решения системы линейных уравнений методом Холесского. |
Содержание работы: |
Разработка алгоритма и программы на С++ для решения системы линейных уравнений методом разложения Холесского с использованием разложения исходной матрицы на верхнюю и нижнюю треуголные матрицы, а далее – прямого исключения и обратной подстановки. |
Исходные данные: |
Система линейных уравнений. |
Результаты работы: |
1. Программа решения СЛАУ методом Холесского. 2. Методика тестирования и отладки программы. |
Литература: |
1. Internet. 2. П. Сильвестер, Р. Феррари Метод конечных элементов для радиоинженеров и инженеров-электриков, М.: Мир, 1986. |
Введение
В данной курсовой работе рассмотрен один из методов вычислений системы линейных алгебраических уравнений – метод Холесского. Данный метод решения СЛАУ является классическим и очень распространённым. К достоинствам метода можно отнести то, что он имеет широкое применение в математике, к примеру используется как вспомогательная часть в методе Монте-Карло для генерации коррелированных случайных величин. Так же этот метод является менее трудоёмким и малоресурсным по сравнению с другими методами.
Описание метода
Метод Холесского
Систему линейных уравнений можно записать в матричном виде:
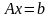 ,
,
где A – квадратная матрица, x и b – векторы-столбцы.
Матрицу A можно представить в виде A=BC , где
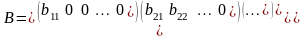 .
.
Тогда элементы bij и cij будут определяться по формулам
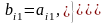 и
и 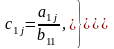
Отсюда искомый вектор x может быть вычислен из цепи уравнений
By=b, Cx=y.
Так как матрицы B и C треугольные, то системы легко решаются, а именно:
 и
и 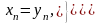
Из формул видно, что числа yi выгодно вычислять вместе с коэффициентам cij . Эта схема вычислений называется схемой Холесского.
Блок-схема метода Холесского
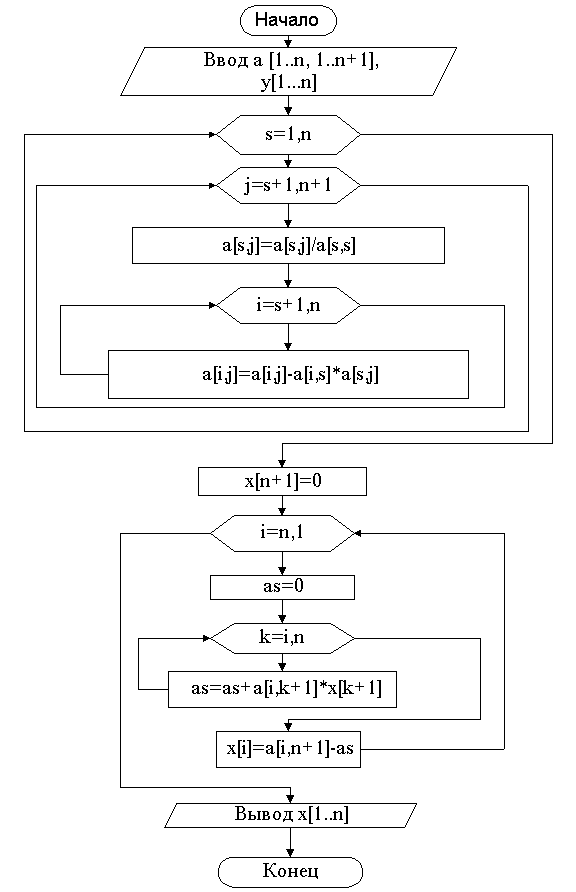
Текст программы и отладка программы
#pragma hdrstop
#include <iostream>
#include <conio.h>
#include <math.h>
using namespace std;
const int NN = 4;
const int pmax = 100;
//---------------------------------------------------------------------------
void multMV(float**, float*, float*, int);
void Nevyazka(float**, float*, float*, float*, int);
float Skalar1(float*, float*, int);
float Skalar2(float**, float*, float*, int);
float Norma(float*, float*, int);
//---------------------------------------------------------------------------
#pragma argsused
int main(int argc, char* argv[])
{//главная программа
float** A, ** AX, ** bX, ** cX;
float D[NN], X[NN], y[NN], err, tmp;
float Xk[NN], Xk1[NN], Rk[NN], Rk1[NN], tk, tk1, ak, ak1, nrm;
int m, p = 1;
A = new float* [NN]; //создание массивов нужных размеров
AX = new float* [NN];
bX = new float* [NN];
cX = new float* [NN];
for (int j = 0; j < NN; j++)
{
A[j] = new float[NN]; AX[j] = new float[NN + 1];
bX[j] = new float[NN]; cX[j] = new float[NN];
}
//Коэффициенты СЛАУ
A[0][0] = 22; A[0][1] = -3; A[0][2] = -8; A[0][3] = 7;
A[1][0] = A[0][1]; A[1][1] = 19; A[1][2] = -6; A[1][3] = 3;
A[2][0] = A[0][2]; A[2][1] = A[1][2]; A[2][2] = 23; A[2][3] = -7;
A[3][0] = A[0][3]; A[3][1] = A[1][3]; A[3][2] = A[2][3]; A[3][3] = 18;
//Вектор правых частей СЛАУ
D[0] = -24; D[1] = 40; D[2] = -84; D[3] = -56;
//Допустимая погрешность численного решения СЛАУ
err = 1e-6;
cout << " A*X=D" << endl;
cout << " A :" << endl;
for (int i = 0; i < NN; i++)
{
for (int j = 0; j < NN; j++) cout << A[i][j] << "; ";
cout << endl;
}
cout << " D :" << endl;
for (int i = 0; i < NN; i++) cout << D[i] << "; ";
cout << endl;
//решение СЛАУ методом Холесского
for (int i = 0; i < NN; i++)
{ //формируем расширенную матрицу AX и вспомогательные массивы
for (int j = 0; j < NN; j++)
{
AX[i][j] = A[i][j];
bX[i][j] = 0; cX[i][j] = 0;
}
AX[i][NN] = D[i]; cX[i][i] = 1;
}
//шаг 1
for (int i = 0; i < NN; i++) bX[i][0] = AX[i][0];
for (int i = 1; i < NN; i++) cX[0][i] = AX[0][i] / bX[0][0];
y[0] = AX[0][NN] / bX[0][0];
//шаги m=2...NN
for (int j = 2; j < NN + 1; j++)
{
m = j - 1;
for (int i = m; i < NN; i++)
{
tmp = AX[i][m];
for (int k = 0; k < m; k++) tmp -= bX[i][k] * cX[k][m];
bX[i][m] = tmp;
}
for (int i = m + 1; i < NN; i++)
{
tmp = AX[m][i];
for (int k = 0; k < m; k++) tmp -= bX[m][k] * cX[k][i];
cX[m][i] = tmp / bX[m][m];
}
tmp = AX[m][NN];
for (int k = 0; k < m; k++) tmp -= bX[m][k] * y[k];
y[m] = tmp / bX[m][m];
}
cout << endl << " B :" << endl;
for (int i = 0; i < NN; i++)
{
for (int j = 0; j < NN; j++) cout << bX[i][j] << "; ";
cout << endl;
}
cout << endl << " C :" << endl;
for (int i = 0; i < NN; i++)
{
for (int j = 0; j < NN; j++) cout << cX[i][j] << "; ";
cout << endl;
}
/* вывод промежуточных результатов для отладки
cout << " Y :" << endl;
for (int j = 0; j < NN; j++) cout << y[j] << "; ";
cout << endl;
*/
//нахождение решения СЛАУ
X[NN - 1] = y[NN - 1];
for (int i = NN - 2; i >= 0; i--)
{
tmp = y[i];
for (int k = i + 1; k < NN; k++) tmp -= cX[i][k] * X[k];
X[i] = tmp;
}
//вывод решения
//cout << endl << "Результат по Холесскому:" << endl;
cout << endl << "Result po Holesskomy:" << endl;
cout.precision(9); //задание числа цифр после запятой при выводе на экран
for (int i = 0; i < NN; i++)
cout << " x" << i + 1 << "=" << X[i] << endl;
//вычисление невязки для решения с 6 знаками после запятой
int ktmp;
for (int i = 0; i < NN; i++) //оставляем 6 знаков после запятой
{
ktmp = X[i] * 1000000.;
X[i] = ktmp / 1000000.;
}
//cout << " Невязка:" << endl;
cout << " Nevyazka:" << endl;
Nevyazka(A, X, D, Rk, NN); //невязка для полученного результата
cout.precision(4); //задание числа цифр после запятой при выводе на экран
/* вывод промежуточных результатов для отладки
for (int i = 0; i < NN; i++)
cout << " x" << i+1 << "=" << X[i] << endl;
*/
for (int i = 0; i < NN; i++)
cout << " r" << i + 1 << "=" << Rk[i] << endl;
//решение СЛАУ методом сопряжённых градиентов
//cout << endl << "Решение методом сопряжённых градиентов:" << endl;
cout << endl << "Reshenie metodom sopryazonnykh gradientov:" << endl;
//начальное приближение (целые части от решения по Холесскому)
for (int j = 0; j < NN; j++)
{
ktmp = X[j]; Xk[j] = ktmp;
}
/* вывод результатов по шагам итерации
cout << " initial vektor X0 (k=0):" << endl;
for (int j = 0; j < NN; j++) cout << Xk[j] << "; ";
cout << endl;
*/
//первое приближение
Nevyazka(A, Xk, D, Rk, NN); //невязка для начального приближения (19)
tk = Skalar1(Rk, Rk, NN) / Skalar2(A, Rk, Rk, NN); //(20)
ak = 1;
for (int j = 0; j < NN; j++) Xk1[j] = Xk[j] - tk * Rk[j]; //(21)
nrm = Norma(Xk, Xk1, NN);
/* вывод результатов по шагам итерации
cout << " vektor X1 (k=1):" << endl;
for (int j = 0; j < NN; j++) cout << Xk1[j] << "; ";
cout << endl;
cout << " norma:" << nrm << endl;
*/
while ((nrm > err) && p < pmax)
{//итерации до достижения заданной точности и максимального числа шагов
Nevyazka(A, Xk1, D, Rk1, NN); //невязка для последнего приближения (22)
tk1 = Skalar1(Rk1, Rk1, NN) / Skalar2(A, Rk1, Rk1, NN); //(23)(26)
ak1 = Skalar1(Rk1, Rk1, NN) / Skalar2(A, Rk, Rk, NN);
ak1 = 1 / (1 - tk1 * ak1 / tk / ak); //(24)
for (int j = 0; j < NN; j++)
X[j] = ak1 * Xk1[j] + (1 - ak1) * Xk[j] - tk1 * ak1 * Rk1[j]; //(25)
for (int j = 0; j < NN; j++) //пересохраняем результаты последних итераций
{
Xk[j] = Xk1[j]; Xk1[j] = X[j]; Rk[j] = Rk1[j];
}
p++;
nrm = Norma(Xk, Xk1, NN);
/* вывод результатов по шагам итерации
cout << " vektor Xk (k=" << p << "):" << endl;
for (int j = 0; j < NN; j++) cout << Xk1[j] << "; ";
cout << endl;
cout << " norma:" << nrm << endl;
*/
}
cout.precision(7); //задание числа цифр после запятой при выводе на экран
//if (p >= pmax) cout << "!!! Точность " << err << " не достигнута !!!" << endl;
if (p >= pmax) cout << "!!! Tochnost " << err << " ne dostignuta !!!" << endl;
else
{
for (int j = 0; j < NN; j++)
cout << " x" << j + 1 << "=" << Xk1[j] << endl;
cout << " by k=" << p << " iterations" << endl;
}
system("pause");
return 0;
}
//---------------------------------------------------------------------------
//процедура умножения матрицы M nxn на вектор V с результатом в векторе R
void multMV(float** M, float* V, float* R, int N)
{
for (int i = 0; i < N; i++)
{
R[i] = 0;
for (int j = 0; j < N; j++)
R[i] += M[i][j] * V[j];
}
}
//---------------------------------------------------------------------------
//процедура нахождения вектора невязки R как M*V-B
void Nevyazka(float** M, float* V, float* B, float* R, int N)
{
multMV(M, V, R, N);
for (int i = 0; i < N; i++)
R[i] -= B[i];
}
//---------------------------------------------------------------------------
//процедура нахождения скалярного произведения векторов
float Skalar1(float* V1, float* V2, int N)
{
float res = 0;
for (int i = 0; i < N; i++)
res += V1[i] * V2[i];
return res;
}
//---------------------------------------------------------------------------
//процедура нахождения скалярного произведения векторов,
//один из которых есть произведение матрицы и другого вектора
float Skalar2(float** M, float* V, float* V2, int N)
{
float res = 0, tmp = 0;
for (int i = 0; i < N; i++)
{
tmp = 0;
for (int j = 0; j < N; j++)
tmp += M[i][j] * V[j];
res += tmp * V2[i];
}
return res;
}
//---------------------------------------------------------------------------
//процедура вычисления нормы разности двух векторов (28)
float Norma(float* V1, float* V2, int N)
{
float res = 0;
for (int i = 0; i < N; i++)
res += pow(V1[i] - V2[i], 2);
return sqrt(res);
}
