курсачи / Kurs_Otc (1)

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РТЭ

Курсовой проект

по дисциплине «Программные средства моделирования»

Тема: «Модуль решения системы линейных уравнений методом ПВР с автоматически выбором оптимальным коэффициента»

Вариант 8

Студент гр. 5201		Ивойлов К.А.
Преподаватель		Синёв А.Е.

Санкт-Петербург

2018

Алгоритм метода: на первой иттерации считается, что каждый x_i = 0, изначально принимается каждая k-я строчка приводится к виду

Тогда значение x_j на каждой иттерации определяется как

Где w – коэффиент корелляции, для метода Зейделя w = 1.

Для метода прямых верхних релаксаций w ϵ [1;2]. Оптимальный коэффициент w_опт определяется по формуле

где λ определяется по формуле

Код программы:

#include "stdafx.h"

#include <conio.h>

#include <cmath>

#include <iostream>

#include <cstdlib>

#include <math.h>

using namespace std;

int main()

{

setlocale(LC_CTYPE, "RUSSIAN");

int i,j,n,k,c,dig;

double **a, *b, *x;

double w, summa, L, Lv, Ln, M_E, Ax, f, vspom;

cout << "Введите размерность матрицы: ";

cin >> n; //Ввод размерности матрицы коэффициентов.

cout<<"Введите погрешность: ";

cin >> M_E; //Ввод погрешности.

//Выделение памяти под матрицу a и векторы b и x

a = new double *[n];

b = new double [n];

x = new double [n];

for(i = 0; i < n; i++)

{

a[i] = new double[n];

for(j = 0; j < n; j++)

{

cout << "a[" << i + 1 << "][" << j + 1 << "] = "; //Ввод коэффициентов матрицы "a".

cin >> a[i][j];

}

}

for(i = 0; i < n; i++)

{

cout << "b[" << i + 1 << "] = "; //Ввод коэффициентов матрицы "b".

cin >> b[i];

}

cout << endl;

for (j = 0; j < n; j++)

{

for (k = 0; k < n; k++)

{

cout << a[j][k] << "\t"; //Вывод на экран введённой матрицы.

}

cout << " | " << b[j] << endl;

}

double *x1 = new double[n];

double *x2 = new double[n];

double *x3 = new double[n];

for (j = 0; j < n; j++) //Обнуление вспомогательных матриц и матрицы корней.

{

x[j] = 0;

x1[j] = 0;

x2[j] = 0;

x3[j] = 0;

}

w = 1;

i = 0;

do

{ //Решение СЛАУ методом Зейделя

i++;

for (j = 0; j < n; j++)

{

summa = 0; //Расчёт корней СЛАУ x

for (k = 0; k < n; k++)

summa = summa + a[j][k] / a[j][j] * x[k];

x[j] = x[j] - w * summa + w * b[j] / a[j][j];

}

for (k = 0; k < n; k++)

{

x3[k] = x2[k];

x2[k] = x1[k];

x1[k] = x[k];

}

}

while ( i < 12 );

cout << endl;

for (j = 0; j < n; j++)

{

cout << "Метод Зейделя: x_" << j+1 << "= " << x[j] << endl;

}

Lv = 0;

Ln = 0;

L = 0;

for (j = 0; j < n; j++)

{

Lv = Lv + pow((x1[j]-x2[j]),2); //Расчёт числителя лямды

Ln = Ln + pow((x2[j]-x3[j]),2); //Расчёт знаменателя лямды

}

L = sqrt(Lv / Ln); //Расчёт лямды

w = 2 / ( 1 + sqrt(1 - L)); //Расчёт коэффициента релаксации

cout << endl << "Коэффицент релаксации w равен: "<< w << endl;

for (j = 0; j < n; j++)

x[j] = 0;

do //Решение СЛАУ методом ПВР

{

Ax = 0;

f = 0;

i++;

for (j = 0; j < n; j++)

{

summa = 0;

for (k = 0; k < n; k++)

summa = summa + a[j][k] / a[j][j] * x[k];

x[j] = x[j] - w * summa + w * b[j] / a[j][j];

}

for (k = 0; k < n; k++)

{

x3[k] = x2[k];

x2[k] = x1[k];

x1[k] = x[k];

}

for (j = 0; j < n; j++)

{

for (k = 0; k < n; k++)

{

Ax = Ax + x[k] * a[j][k];

}

f = f + b[j];

}

vspom = abs(Ax - f);

}

while ( vspom > M_E);

for (j = 0; j < n; j++) //Вывод корней СЛАУ

{

cout << "ПВР: x_" << j+1 << "= " << x[j] << endl;

}

_getch();

return 0;

}

Пример:

3х₁ + х₂ = 10

2х₁ + 8х₂ = 14

После преобразования получаем:

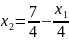
В правые части уравнений соответственно подставляем x₁ = x₂ = 0.

В данной реализации метода заложено, что методом Зейделя будет совершено 12 иттераций, после чего рассчитывается оптимальный коэффициент релаксации w. Коэффициент, рассчитанный программой, совпал с рассчитанным вручную.

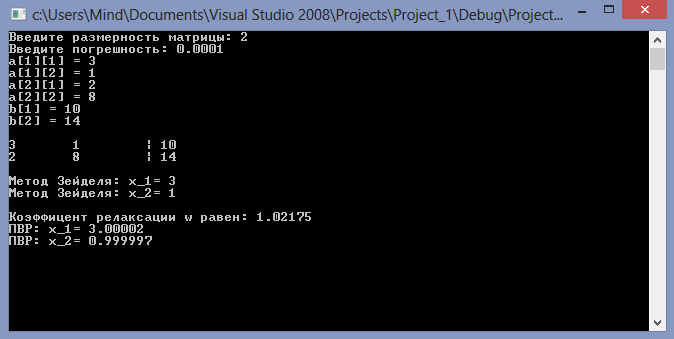
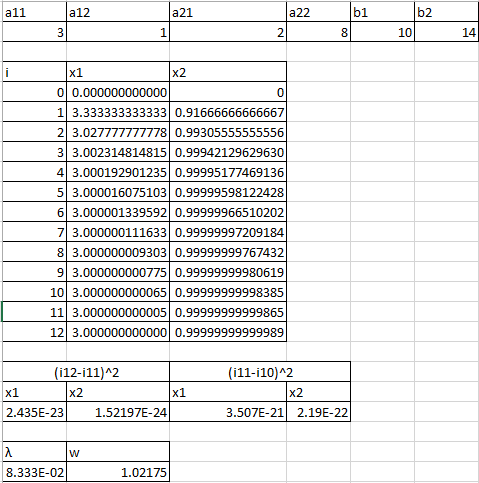
В дальнейшем программа рассчитывает корни уравнений до тех пор, пока погрешность вычислений не станет меньше заданной пользователем значением.