курсачи / Kursovaya_POtapova

МИНОБРНАУКИ РОССИИ

Государственное образовательное учреждение

высшего профессионального образования

Санкт-Петербургский государственный электротехнический университет

«ЛЭТИ» им. В.И. Ульянова ( Ленина)

ФАКУЛЬТЕТ ЭЛЕКТРОНИКИ (ФЭЛ)

КАФЕДРА Радиотехнической электроники

КУРСОВАЯ РАБОТА (ПРОЕКТ)

По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ

На тему: Разработка модуля программы анализа электронного прибора

(указывается обобщенная тема)

Вариант № 14

Выполнила			Оценка
студентка гр. №	5201		Проверил	Синев А. Е.
	Потапова М.А.			(ФИО)
	(ФИО)		Дата	18.04.2019

САНКТ-ПЕТЕРБУРГ

2019 г.

ЗАДАНИЕ на курсовую работу

По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ

Вариант 14.

Название курсовой работы:	Модуль расчёта пространственного заряда в узлах 3D сетки.
Содержание работы:	Разработка алгоритма и С++ - программы распределения заряда электронного потока по узлам 3D сеточной области.
Исходные данные:	Замкнутая поверхность, заданная набором плоских треугольников, скорости и токи трубок.
Результаты работы:	1. Программа расчёта объемного заряда в узлах 3D сетки (точка пересечения прямой и треугольника). 2. Методика тестирования и отладки программы.
Литература:	1. Internet. 2. Моделирование полупроводниковых приборов и технологических процессов. Последние достижения. Под ред. Д. Миллера, М.: Радио и связь, 1989.

1. Цель и задача выполнения курсового проекта

Цель выполнения курсового проекта: Получение практических навыков программного моделирования электронной компонентной базы.

Задача выполнения курсового проекта: разработка алгоритма и С++ программы расчета технологической операции в соответствии с заданными темой работы и исходными данными.

Теоретические сведения:

Основной задачей было выяснение точки пересечения прямой и плоскости треугольника (в 3хмерном пространстве), для этого мне потребовались:

формула вычисления направляющего вектора по 2м известным точкам, лежащим на прямой;

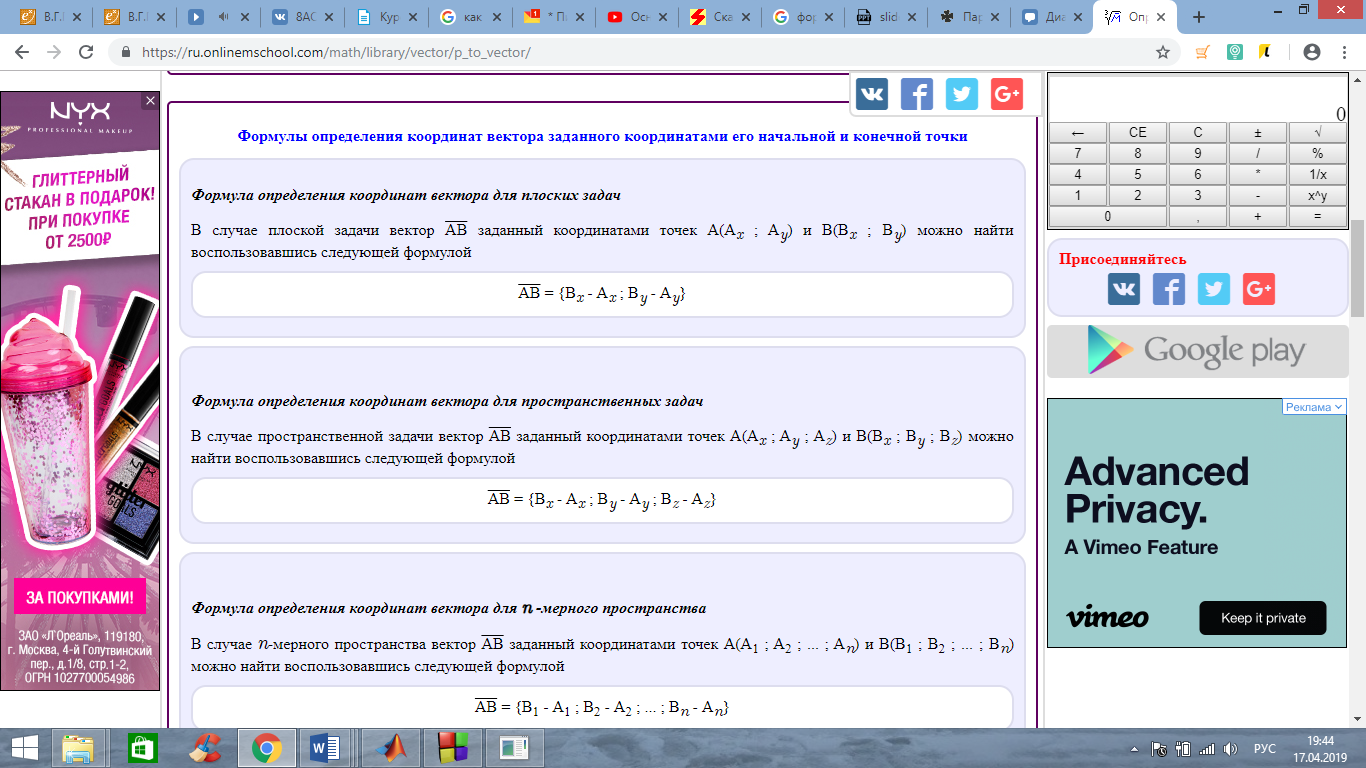
формула нахождения вектора нормали к плоскости треугольника. Для ее нахождения мне необходимы коэффициенты а,б,с и д из найденного уравнения плоскости треугольника( по 3м известным точкам).

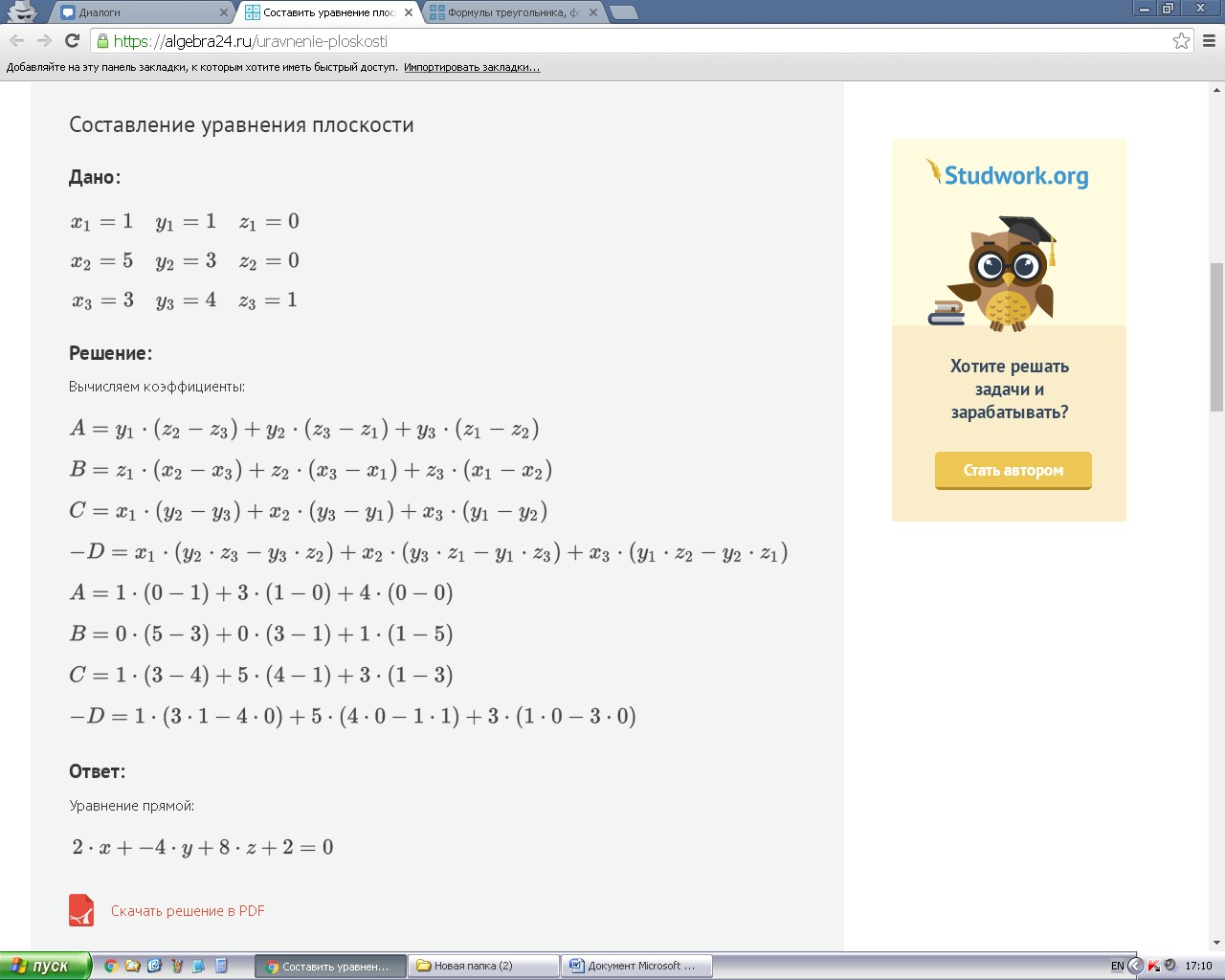
Соответственно вектор нормали к плоскости треугольника имеет координаты а,б и с из данного уравнения.

Далее выявим случай, когда прямая пересекает плоскость

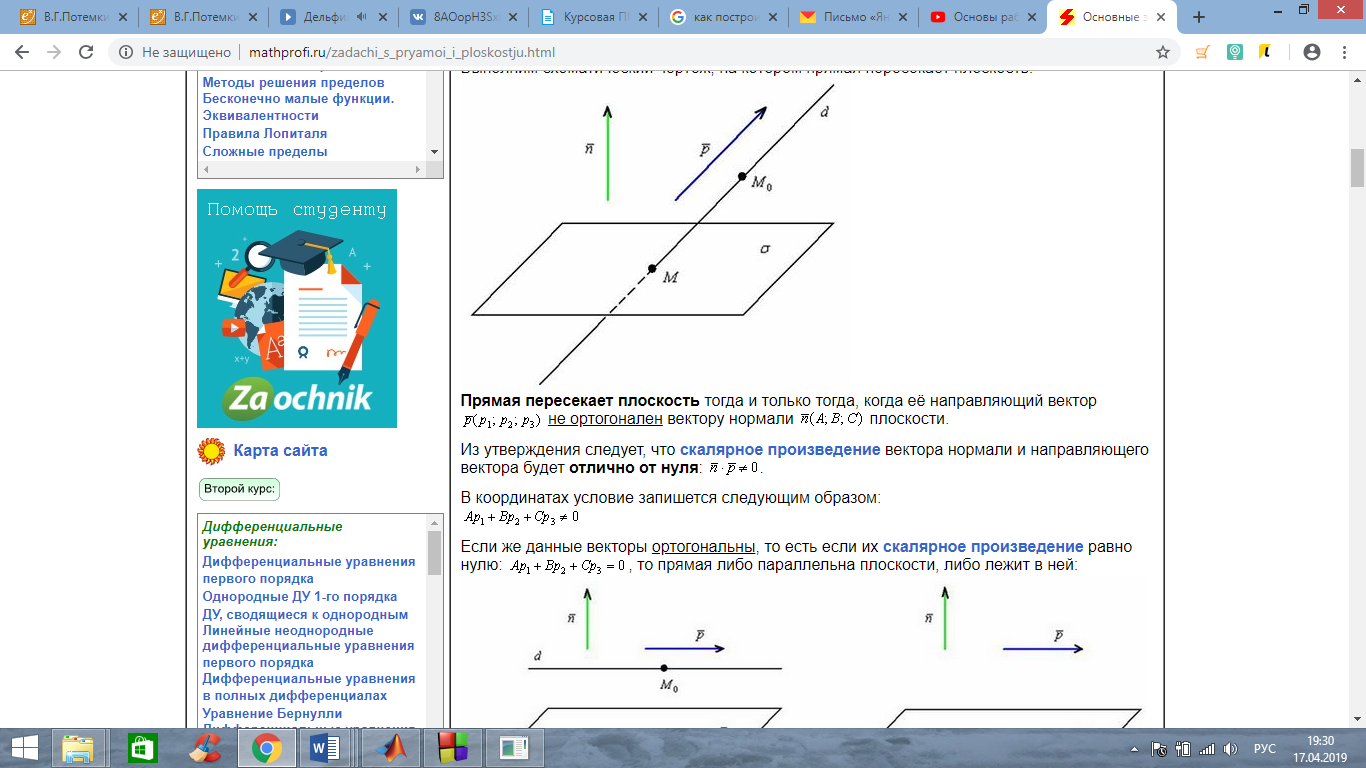
То есть, если скалярное произведение направляющего вектора прямой и вектора нормали плоскости треугольника не равно 0, то прямая пересекает плоскость.

Запишем параметрическое уравнение прямой

параметрическое уравнение прямой, где лямбда –параметрический коэффициент.

Точка пересечения прямой и плоскости будет иметь координаты x,y,z.

Теперь необходимо определить принадлежность точки к плоскости треугольника.

Найдем длину сторон треугольника по формуле вычисления площади треугольника через его стороны и полупериметр

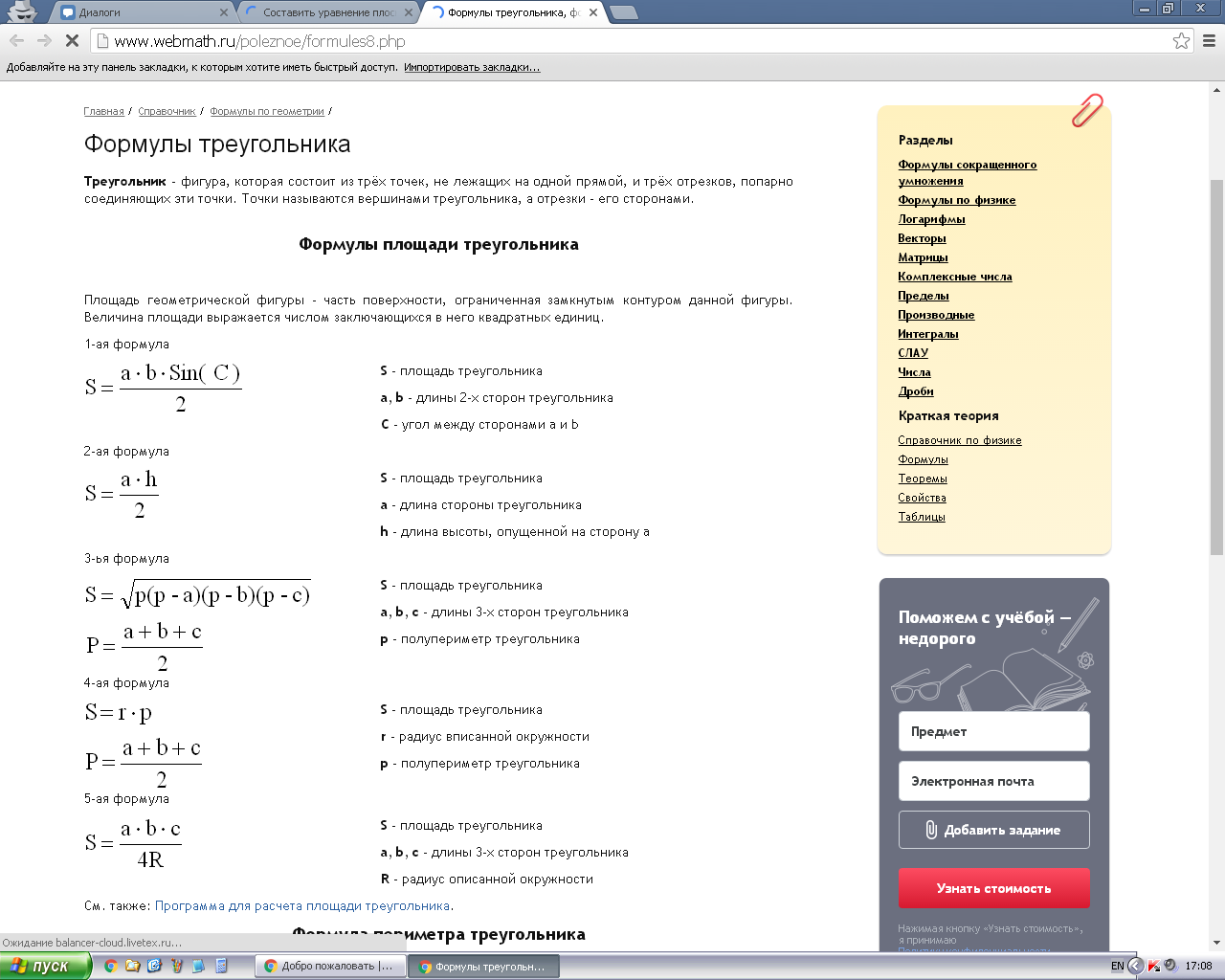
Вычислим площадь заданного треугольника ABC, а так же площади треугольников АВР, АРС и РВС (точка Р – точка пересечения прямой и плоскости треугольника АВС).

В случае , если Sabc >= Sapb+Sapc+Sbpc – точка принадлежит плоскости треугольника, в противном случае не принадлежит.

Текст программы:

#include <math.h>

#include <fstream>

#include <iostream>

#include <cstring>

using namespace std;

int main()

{

double x1,y1,z1,x2,y2,z2,x21,y21,z21,a,b,c,d,X,K,L,XX,y,x,cosin,Z,t,x0,y0,z0;

//вводим точки плоскости, те заданного треугольника

int A[3]= {1,1,0};

int B[3]= {5,3,0};

int C[3]= {3,4,1};

cout << "Vvedite tochki nachala i kontsa lejashie na pryamoy :" << endl;

cin >>x1>>y1>>z1>>x2>>y2>>z2;

// Формируем вектор (прямая) из двух координат точек

x21=x2-x1;

y21=y2-y1;

z21=z2-z1;

double Pramaya[3]= {x21,y21,z21};

// Наждение вектора нормали к плоскости. Для этого возьмем коэфициенты из уравнения плоскости aх+bу+cz+d=0

a=2; b=-4; c=8; d=2;

double n[3]= {x21,y21,z21}; //нормаль плоскости треугольника

//Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор

//не ортогонален вектору нормали плоскости.

//введем обозначения для косинуса угла между веторами

X=x21*a+y21*b+z21*c;

K=x21*x21+y21*y21+z21*z21;

L=a*a+b*b+c*c;

x = sqrt(K);

y = sqrt(L);

cosin = X /( y * x) ;

// найдем скалярное произведение векторов

Z = K*L*cosin;

if (Z == 0) { //прямая не пересекает, так как векторы ортогональны.

cout << "vektory ortogonalny" << endl;

} else { // иначе

cout << "Pryamaya peresekaet ploskost treugolnika" << endl;

};

// запишем параметрическое уравнение прямой с коэфф-том

t =((-a*x1-b*y1-c*z1-d)/(a*(x2-x1)+b*(y2-y1)+c*(z2-z1)));

x0=(x2-x1)*t+x1;

y0=(y2-y1)*t+y1;

z0=(z2-z1)*t+z1;

double P[3]= {x0,y0,z0};

//Нужно определить прнадлежность точки к плоскости треугольника.

//Найдем длину сторон треугольника

double AB,BC,CA,Pabc,AP,BP,CP,Papb,Papc,Pbpc,Sabc,Sapb,Sapc,Sbpc;

AB=sqrt(20);//Длина стороны АВ

BC=sqrt(6);//Длина стороны ВС

CA=sqrt(14);//Длина стороны ВС

Pabc=(AB+BC+CA)/2;//Периметр треугольника АВС

AP=sqrt((x0-1)*(x0-1)+(y0-1)*(y0-1)+(z0-0)*(z0-0));//Длина стороны АР

BP=sqrt((x0-5)*(x0-5)+(y0-3)*(y0-3)+(z0-0)*(z0-0));//Длина стороны ВР

CP=sqrt((x0-3)*(x0-3)+(y0-4)*(y0-4)+(z0-1)*(z0-1));//Длина стороны СР

Papb=(AP+BP+AB)/2;//Периметр треугольника АРВ

Papc=(AP+CP+CA)/2;//Периметр треугольника АРС

Pbpc=(BP+CP+BC)/2;//Периметр треугольника РВС

Sabc=sqrt(Pabc*(Pabc-AB)*(Pabc-BC)*(Pabc-CA));//Площадь треугольника АВС

Sapb=sqrt(Papb*(Papb-AP)*(Papb-BP)*(Papb-AB));//Площадь треугольника АВР

Sapc=sqrt(Papc*(Papc-AP)*(Papc-CP)*(Papc-CA));//Площадь треугольника АРС

Sbpc=sqrt(Pbpc*(Pbpc-BP)*(Pbpc-CP)*(Pbpc-BC));//Площадь треугольника РВС

if (Sabc>=Sapb+Sapc+Sbpc) {

cout << "tochka P prinadl ploskosty treugolnika" << "P=" <<x0 <<"," <<y0<<", "<<z0<< endl;

}

else

{cout << "tochka P ne prinadl ploskosty treugolnika" << endl;

};

return 0;

}

Тестирование и отладка программы:

Для проверки результатов воспользуемся программной средой Matlab для построения графиков с различным расположением прямой и плоскости треугольника.

Построим пересечения прямой и плоскости для разных случаев:

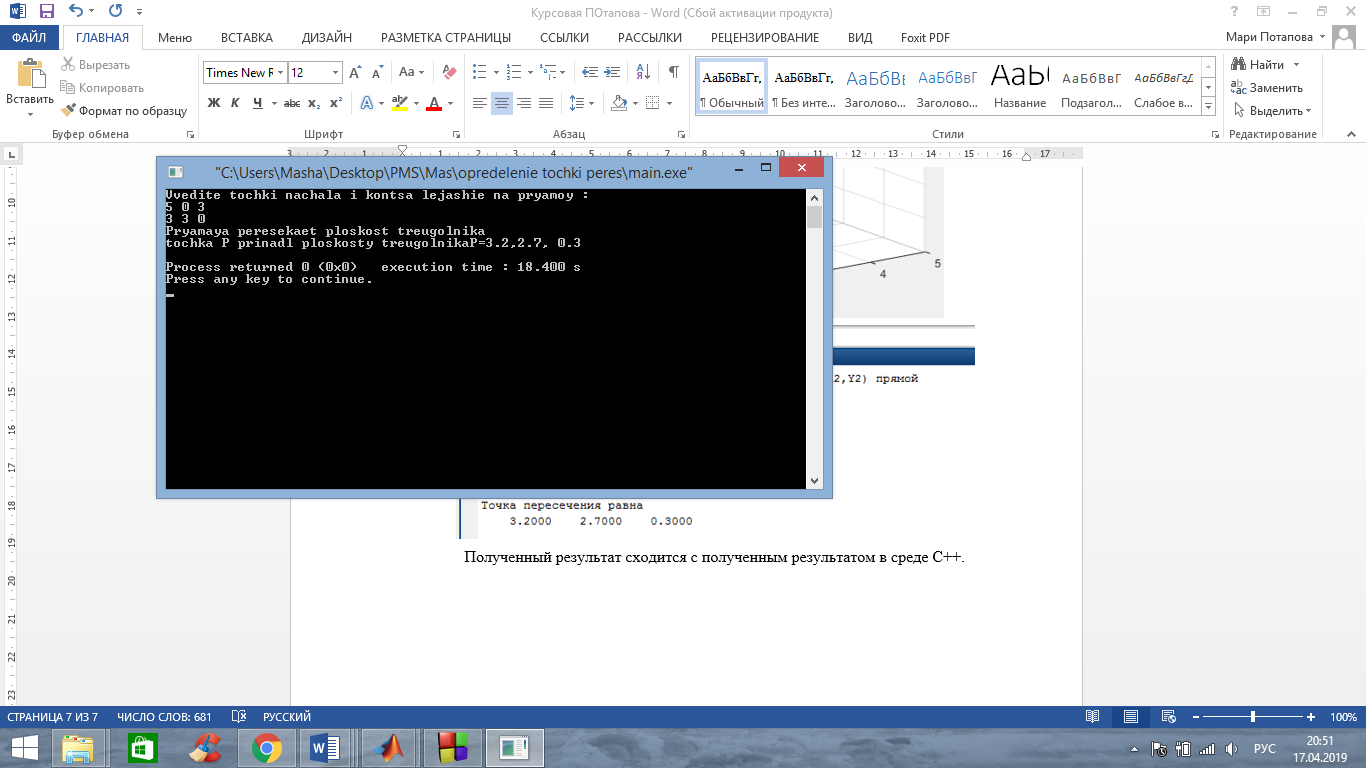
А) Координаты двух точек прямой P1(5,0,3) и Р2(3,3,0). Прямая пересекает треугольник, точка пересечения лежит в плоскости треугольника.

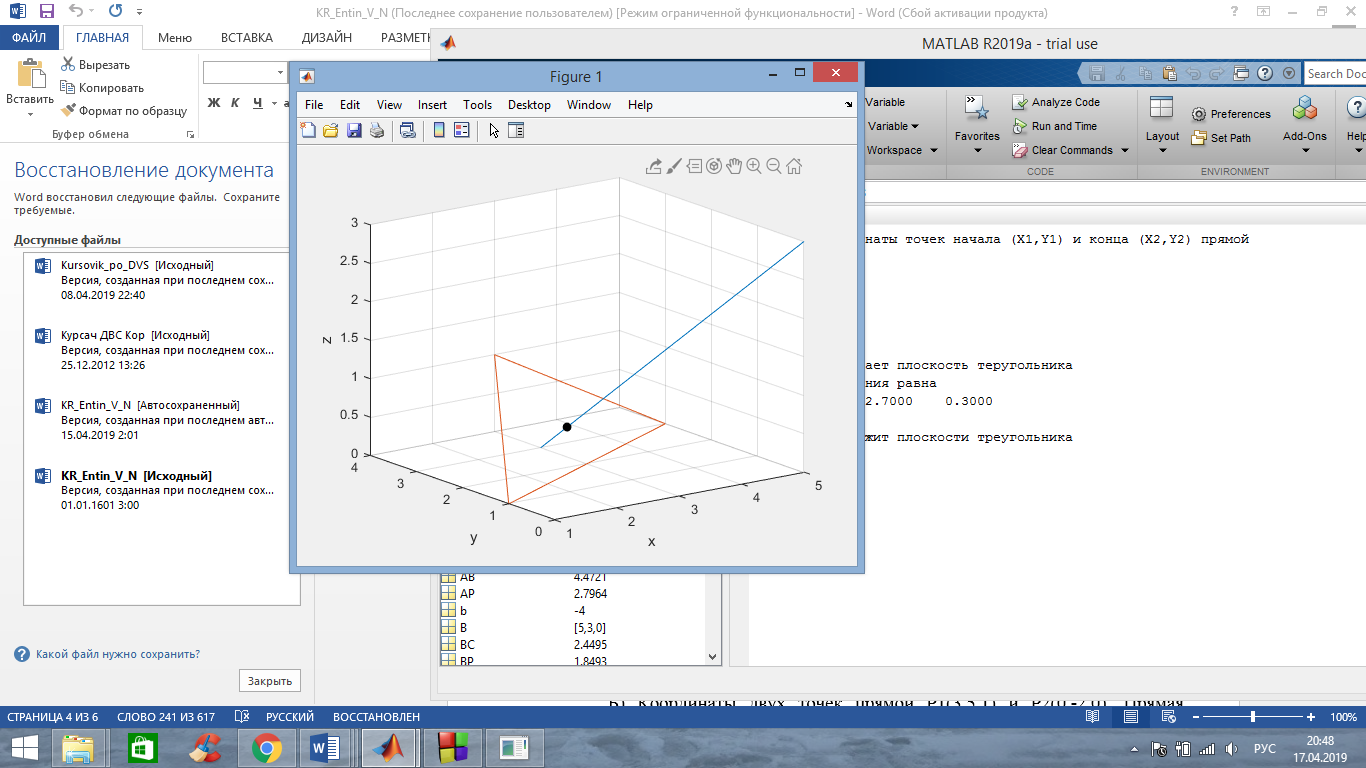
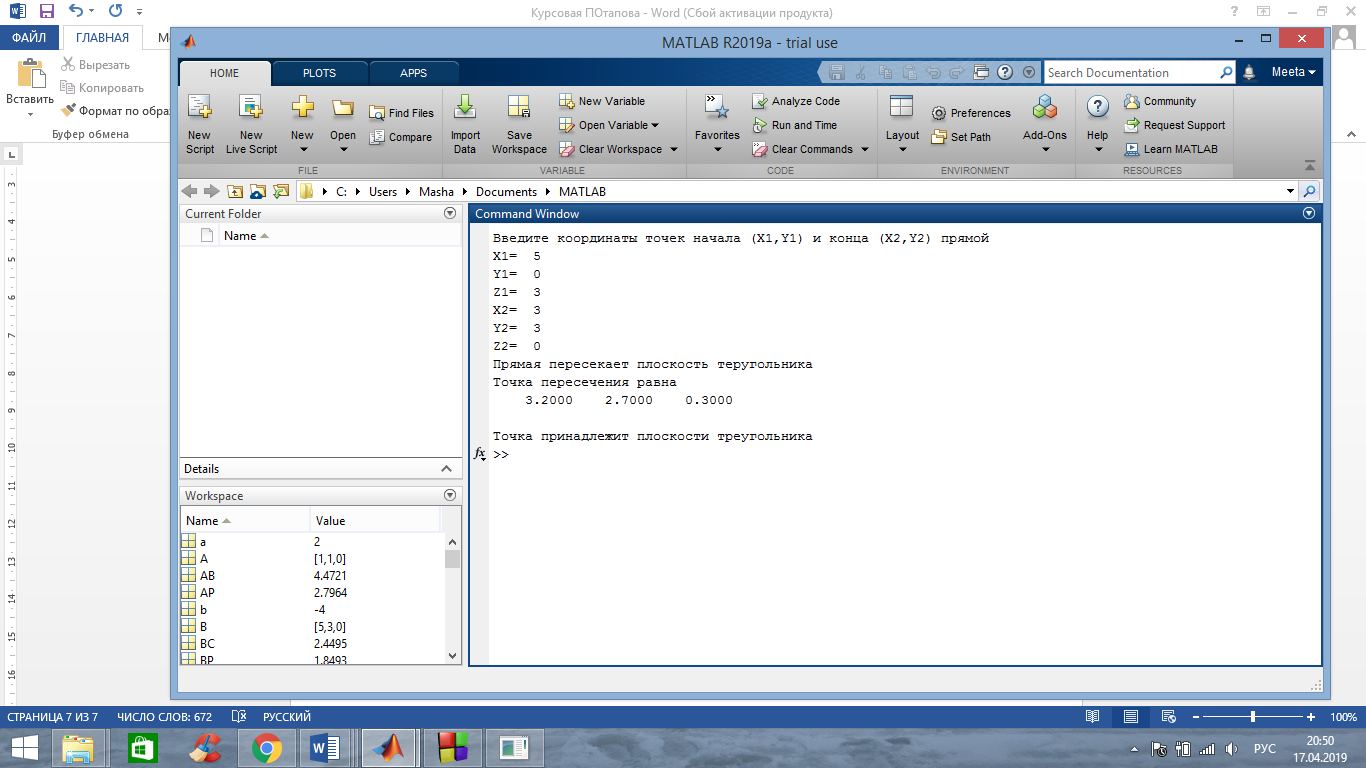
Полученный результат сходится с полученным результатом в среде С++.

Б) Координаты двух точек прямой P1(3,5,1) и Р2(0,-2,0). Прямая пересекает треугольник, точка пересечения не лежит в плоскости треугольника.

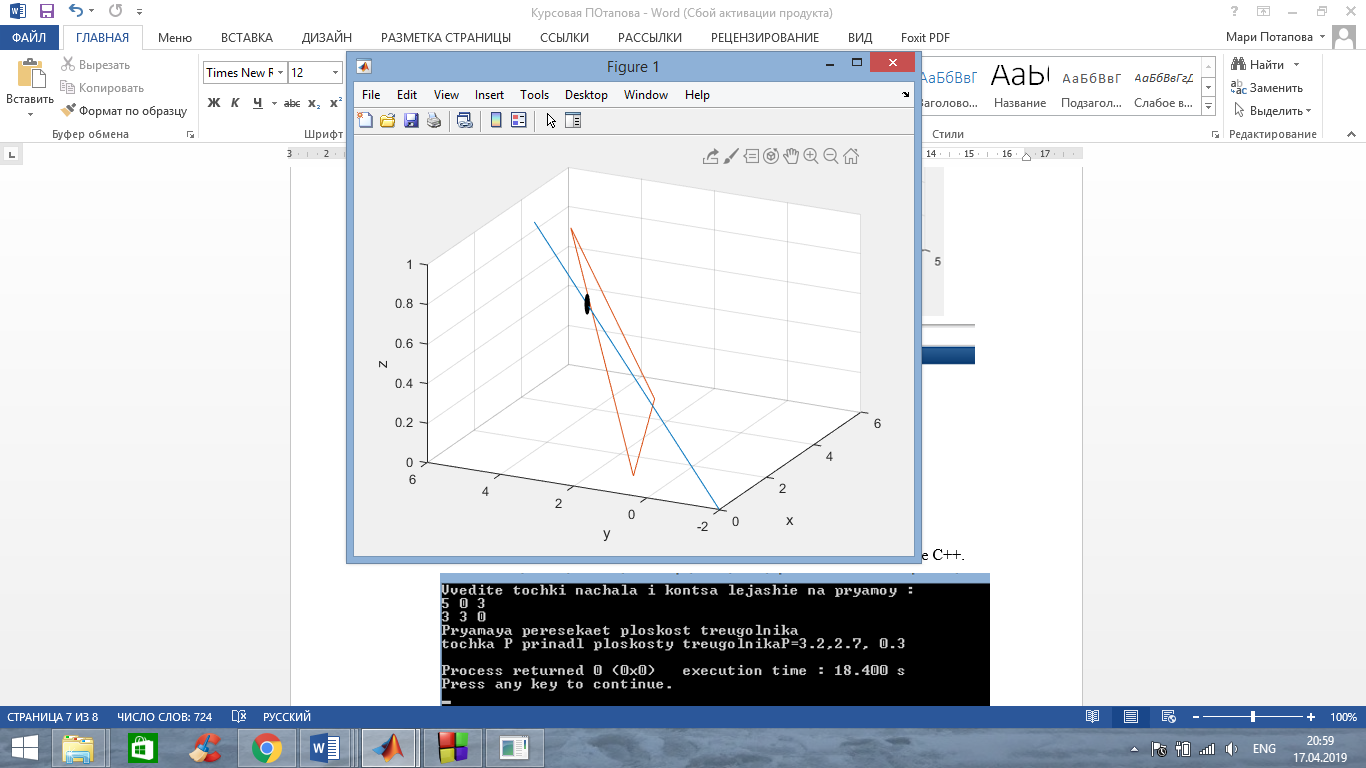
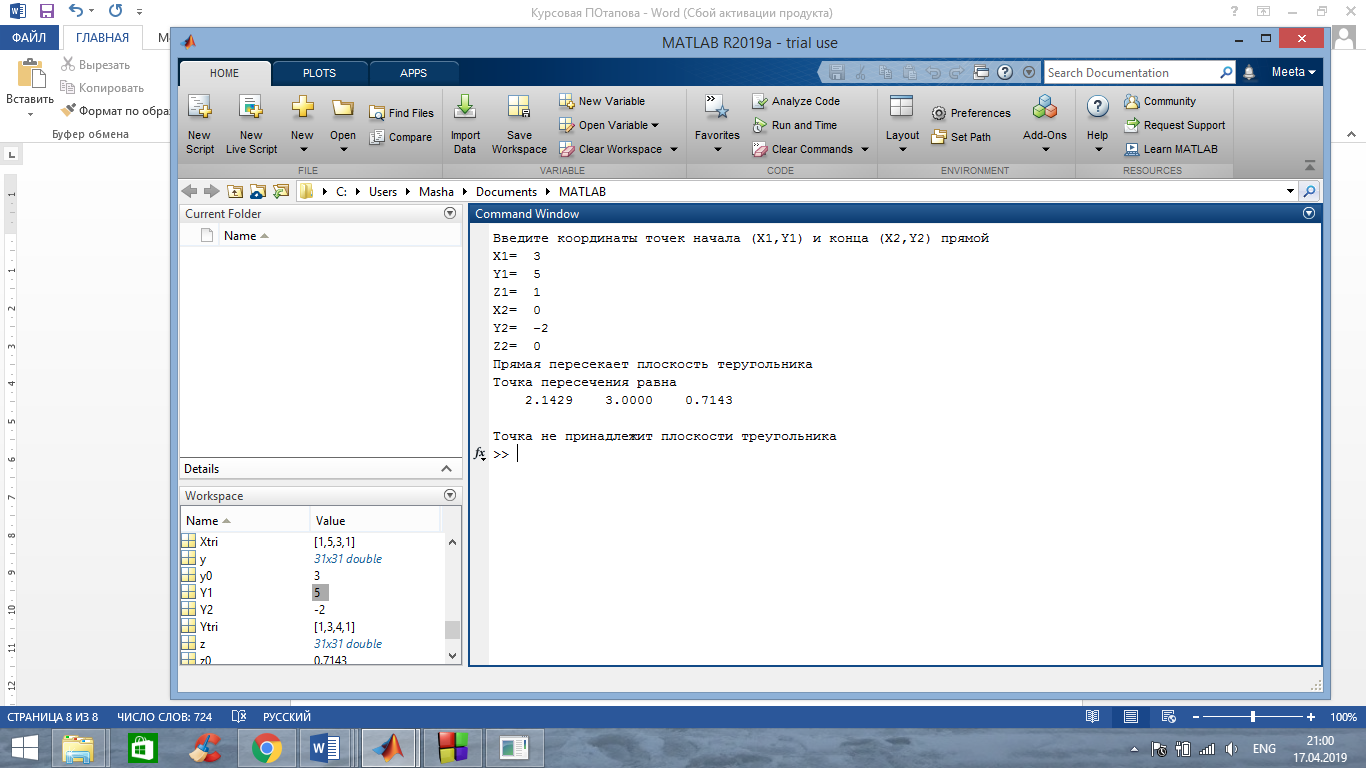
Полученный результат сходится с полученным результатом в среде С++.

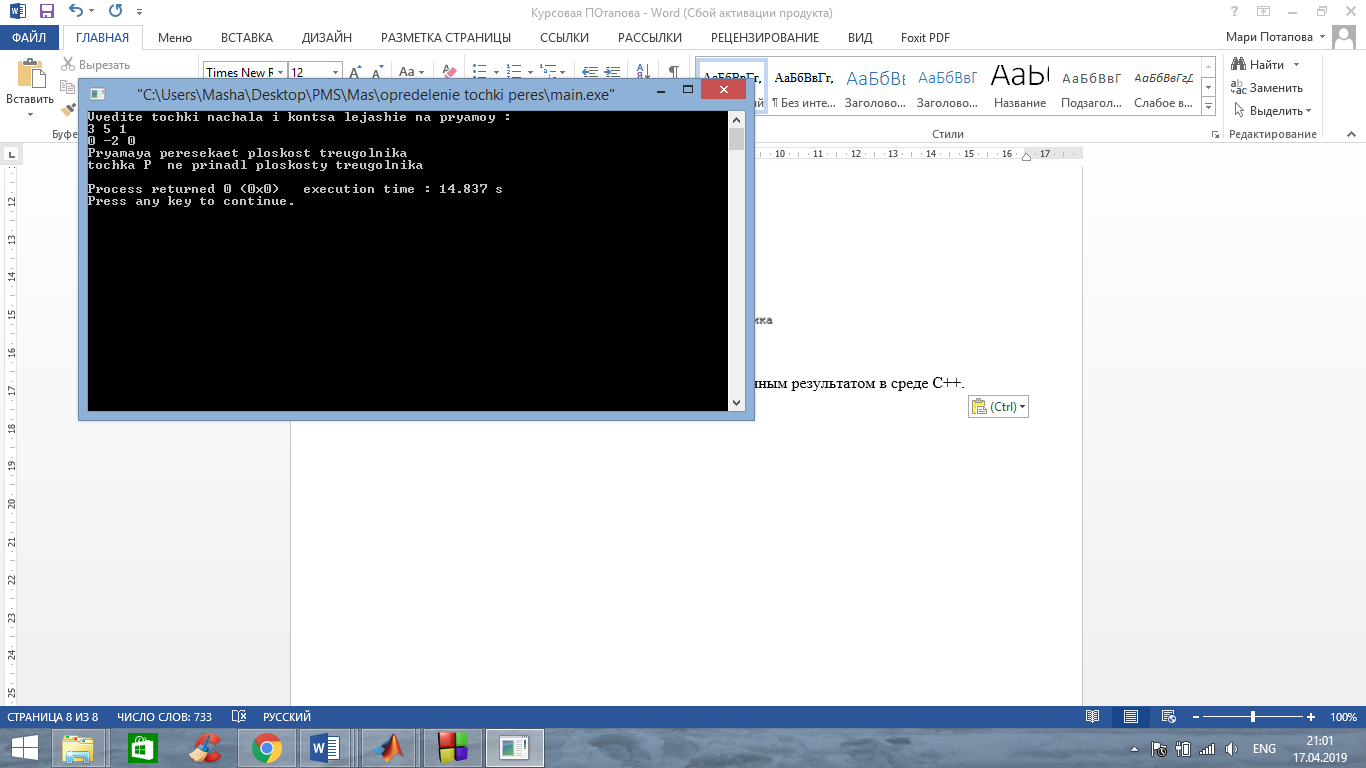
В) Координаты двух точек прямой P1(6,1,2) и Р2(4,2,3). Прямая не пересекает треугольник.

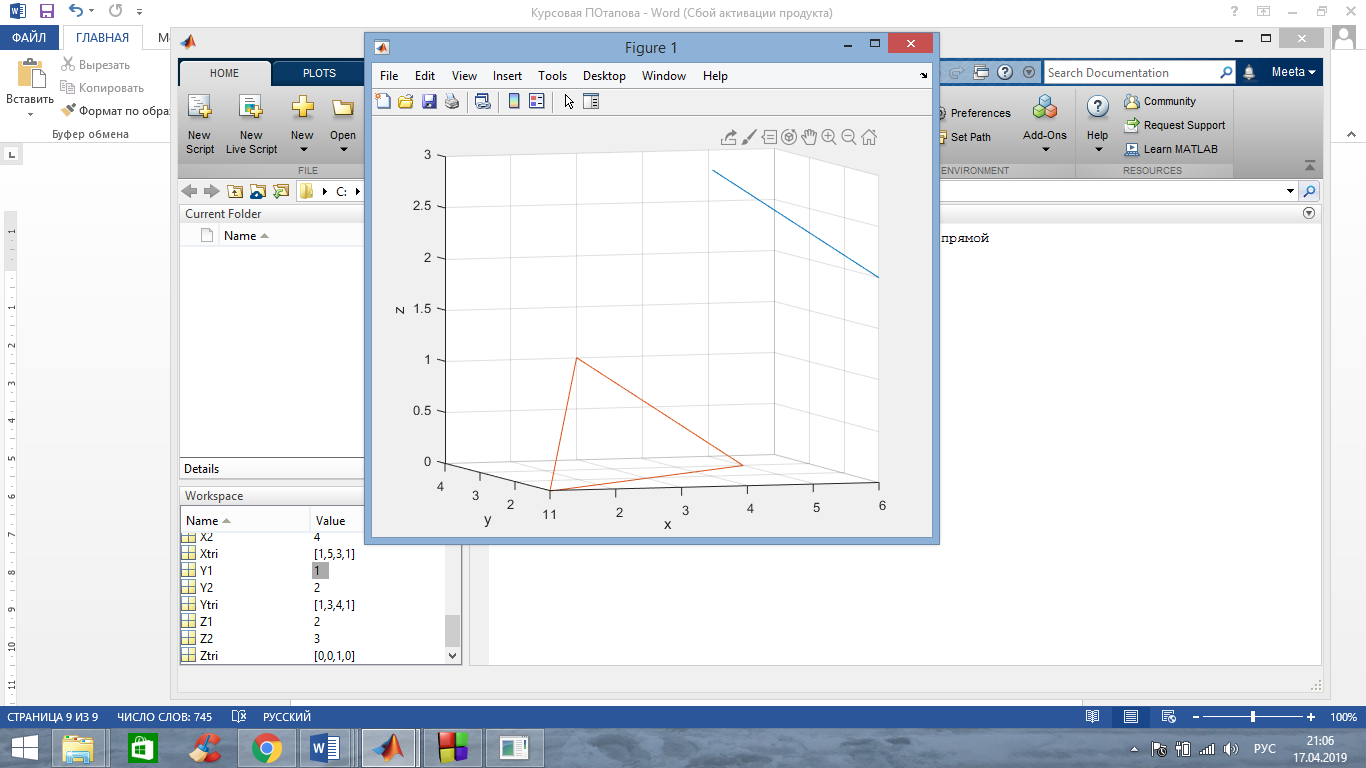
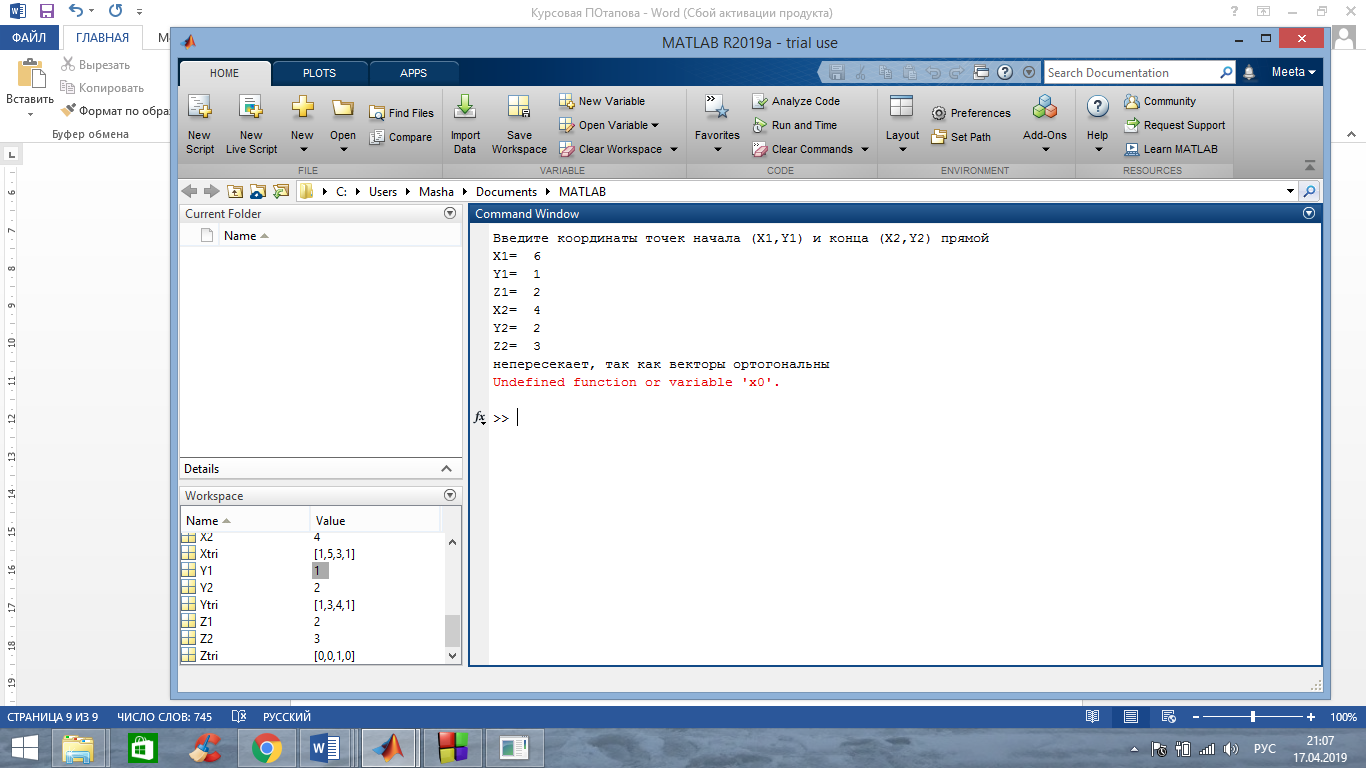
Полученный результат сходится с полученным результатом в среде С++.

Отладка программы выполнена, т.к. программа работает без ошибок.

Вывод: в данной работе рассматривалось пересечение прямой и плоскости треугольника. Было рассмотрено три случая.

Первый случай изображен на рисунке 1, когда прямая пересекает плоскость треугольника. В этом случае направляющий вектор прямой не ортогонален нормали плоскости треугольника, точка лежит в плоскости треугольника.

Второй случай изображен на рисунке 2, когда прямая пересекает плоскость треугольника, но при этом точка пересечения не принадлежит плоскости треугольника.

Третий случай изображен на рисунке 3, когда прямая не пересекает плоскость треугольника. Направляющий вектор прямой ортогонален нормали плоскости треугольника.