
Филатов Лабораторная работа №7
.docxЛабораторная работа № 3.
Элементы теории ошибок измерений.
Задание 7.
Обработка ряда результатов равноточных измерений.
Решение задач по теории ошибок измерений.
Содержание задания:
Перечислить последовательность операций и формулы* для вычислений при обработке ряда результатов равноточных измерений.
Ответ:
Последовательность обработки:
1.Определение наиболее надёжного значения из результатов измерения.
Вычисление среднего арифметического из результатов измерений по формуле
Хср.=
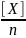 = X0
+
= X0
+
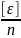 ,
где
εn
= Xn
– X0
,
где
εn
= Xn
– X0
2.Оценка точности
Определение средней квадратической ошибки одного измерения
m
=
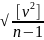 где
vn
= Xn
- Хср
где
vn
= Xn
- Хср
Определение средней квадратической ошибки наиболее надёжного значения
M
=
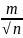 Абсолютная
M
Абсолютная
M
Относительная
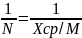
Обработать ряды результатов равноточных измерений длин линий D и горизонтальных углов β
(Таблицы №1 и №2, вариант №….. индивидуального задания).
Ответ. (Результаты вычислений поместить в таблицы № 1 и № 2).
Таблица №1. Обработка равноточных измерений длины линии.
Вариант №9
№№ Результатов измерений |
Результаты измерений длины линии D в [м] |
Отклонения от наименьшего значения ε в [см] |
Уклонения от арифметической средины v в [см] |
Формулы и результаты вычислений |
||
1 |
2 |
3 |
4 |
5 |
||
1 |
224,55 |
26 |
1 |
X0 = 224,29 м [X] = 1571,81 [ε] = 178 см = 1,78 м ; n=7 Хср (точ) = X0 + =224,544 м Хср (окр) = 224,54 м β = Хср (точ) - Хср (окр) =0,004м [v]=3 см=0,03 м Контроль [v] = 0 или [v] = βn [v]=0,004 м * 7=0,028 м=0,03 м Контроль выполнен m =
m = 0,165 м=0,2м M = ; M = 0,076=0,08
|
||
2 |
224,70 |
41 |
16 |
|||
3 |
224,29 |
0 |
-25 |
|||
4 |
224,52 |
23 |
-2 |
|||
5 |
224,72 |
43 |
18 |
|||
6 |
224,66 |
37 |
12 |
|||
7 |
224,37 |
8 |
-17 |
|||
D наиб.надёжн. = 224,54 |
1/N= 1:2807 |
|
||||
Таблица №2. Обработка равноточных измерений горизонтального угла
№№ Результатов измерений |
Результаты измерений гор.угла β [˚ ˈ] |
Отклонения от наименьшего значения ε в [ˈ] |
Уклонения от арифметической средины v [ˈ] |
Формулы и результаты вычислений |
||
1 |
2 |
3 |
4 |
5 |
||
1 |
23° 53,8’ |
0 |
-1.7 |
X0 = 23° 53,8′ [X] = 167° 47′ [ε] =11,6′ Хср (точ) = X0 + = 23° 55,46′ Хср (окр) =23° 55,5′ β= Хср (точ) - Хср (окр) = -0,04′ [v]=-0,3′ Контроль [v] = 0 или [v] = βn [v]=-0,04′ * 7=-0,28′ =-0.3′ Контроль выполнен m = =18.71′ m = 1,765′=1,77’ M = ; M = 0,669′=0,7’ |
||
2 |
23° 57,0’ |
3,2 |
1.5 |
|||
3 |
23° 56,8’ |
3 |
1.3 |
|||
4 |
23° 54,0’ |
0,2 |
-1.5 |
|||
5 |
23° 53,8’ |
0 |
-1.7 |
|||
6 |
23° 54,8’ |
1 |
-0.7 |
|||
7 |
23° 58,0’ |
4,2 |
2.5 |
|||
β наиб.надёжн = 23° 55.5’ |
M = 0,7’ |
|||||
Привести формулы* для вычислений средних квадратических ошибок функций измеренных аргументов


Решить задачи:
Найти формулы* относительных средних квадратических ошибок приращений координат ∆ х и ∆у
Ответ:
∆х = S*cosα
∆y = S*sinα
m∆х2=(∂∆x/∂S)2ms2+(∂∆x/∂α)2mα2 ;
m∆х =√(cosα*ms)2+(S*sinα* (mα /ρ))2
1/N = m∆х / ∆х
m∆y2=(∂∆y/∂S)2ms2+(∂∆y/∂α)2mα2
m∆y =√(sinα*ms)2+(S*cosα* (mα /ρ))2
1/N = m∆y / ∆y
где m∆х – ско приращения координаты X
m∆y - ско приращения координаты Y
ms – ско горизонтального проложения
mα - ско дирекционного угла
S-горизонтальное проложение;
α-дирекционный угол
∆x,∆y -приращение координат;
ρ-величина постоянная
Выполнил студ КиГ 1-2б
Филатов М.Ю.
2020

 =1643
см2=0,1643
м2
=1643
см2=0,1643
м2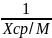 =
0,004
=
0,004