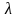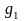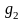Федеральное агентство связи Ордена

Трудового Красного Знамени

федеральное бюджетное образовательное учреждение высшего образования

«Московский Технический Университет Связи и Информатики»

(МТУСИ)

Кафедра Информатики

Предмет: Вычислительные модели

Лабораторная работа № 6

Тема:

«Многомерная оптимизация»

Вариант 00

Выполнил:

Проверил(а): Величайший преподаватель

_________________

Москва 0000

Задание

1. Выбрать индивидуальное задание из табл. 1.8-1 для решения задачи оптимизации функции нескольких переменных:

• функцию–f(x, y);

• метод оптимизации для «ручного расчета» – определяется значением параметра p;

• метод оптимизации для «расчета на ПК»– значения параметровt и r.

2. Проверить условия существования точки минимума заданной функции f(x).

3. Решить задачу многомерной оптимизациианалитическим методом.

4. Выбрать начальную точкуx₀, y₀итерационного процесса оптимизации.

5. Решить задачу оптимизации« ручным расчетом» (3 итерации)выбранным методом.

6. Вычислить погрешности

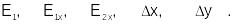
7. Составить схему алгоритма, программу решения задачи оптимизации и провести контрольное тестирование.

8. Решить задачу многомерной оптимизации «расчетом на ПК»при точности определения минимума E=0.1, 0.05, 0.01, 0.001.

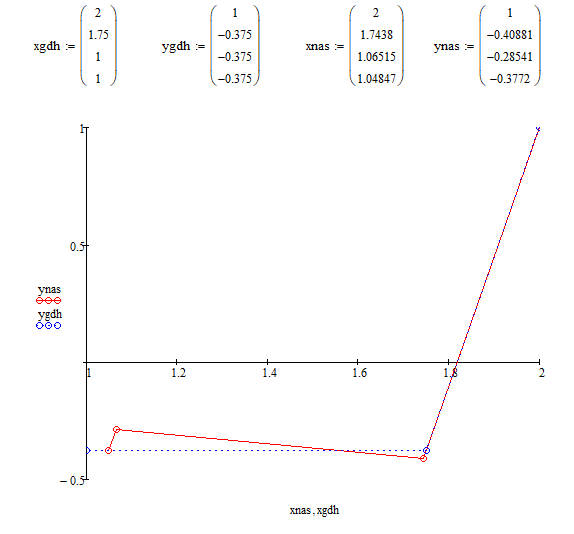
9. Построить траекторию поиска минимума по результатам « расчетана ПК» и изобразить схематически линии уровня, проходящие через точки траектории. На графике указать точку минимума, найденную в п.3 задания.

p=1 метод ГДШ ручной расчет: t=3 метод НСА на ПК

2. Проверка существования минимума функции

Всякий глобальный минимум выпуклой функции является одновременно и локальным.

Проверить, что функция 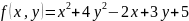является выпуклой на множестве R.

Матрица Гессе для функции :

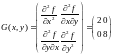
а угловые миноры:

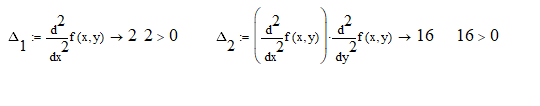
Таким образом, функция 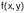- выпуклая на множестве R.

2. Решение задачи многомерной оптимизации аналитическим методом

Необходимые условия существования точки экстремума:

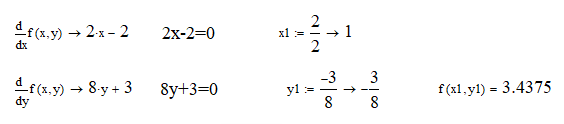
2. Выбор начальной точки итерационного процесса численного решения задачи многомерной оптимизации

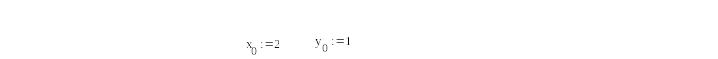
2. Решение задачи численной оптимизации ГДШ «ручным расчетом»

Произведем вычисления, а результаты представим в табл.

k	x	y
1	2	1	0	2	11	12
2	1.75	-0.375	0.125	1.5	0	4
3	1	-0.375	0.5	0	0	3.4375
4	1	-0.375	0.5	0	0	3.4375

Xmin = 1, Ymin = -0.375, f(Xmin,Ymin)= 3.4375

2. Погрешности после трех итераций

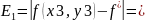0

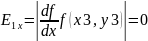
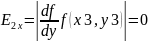
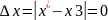
2. Схема Алгоритма и программа для решения задачи оптимизации

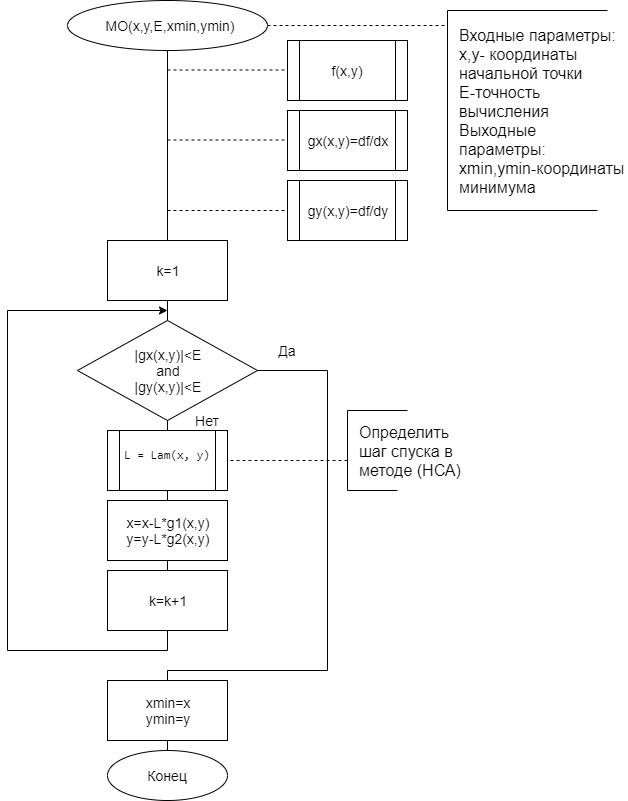
8) Решение задачи оптимизации на ПК (НСА)

Программный код

Option Strict On

Option Explicit On

Imports System.Math

Public Class Form1

Function Lam(ByVal x As Double, ByVal y As Double) As Double

Dim Lamda As Double

Lamda = (4 * x ^ 2 - 8 * x + 64 * y ^ 2 + 48 * y + 13) / (8 * x ^ 2 - 16 * x + 512 * y ^ 2 + 384 * y + 80)

Return Lamda

End Function

Function f(ByVal x As Double, ByVal y As Double) As Double

Dim fun As Double

fun = x ^ 2 + 4 * y ^ 2 - 2 * x + 3 * y + 5

Return fun

End Function

Function gx(ByVal x As Double) As Double

Dim dx As Double

dx = 2 * x - 2

Return dx

End Function

Function gy(ByVal y As Double) As Double

Dim dy As Double

dy = 8 * y + 3

Return dy

End Function

Sub MO(ByVal x As Double, ByVal y As Double, ByVal eps As Double, ByRef xmin As Double, ByRef ymin As Double)

Dim k, L, f1 As Double

k = 1

ListBox1.Items.Add(k)

ListBox2.Items.Add(eps)

ListBox3.Items.Add(Format(x, "0.00000"))

ListBox4.Items.Add(Format(y, "0.00000"))

ListBox5.Items.Add(Format(f1, "0.00000"))

ListBox7.Items.Add(Format(gx(x), "0.00000"))

ListBox8.Items.Add(Format(gy(y), "0.00000"))

Do Until Abs(gx(x)) < eps And Abs(gy(y)) < eps

L = Lam(x, y)

x = x - L * gx(x)

y = y - L * gy(y)

f1 = f(x, y)

k = k + 1

ListBox1.Items.Add(k)

ListBox3.Items.Add(Format(x, "0.00000"))

ListBox4.Items.Add(Format(y, "0.00000"))

ListBox5.Items.Add(Format(f1, "0.00000"))

ListBox6.Items.Add(Format(L, "0.00000"))

ListBox7.Items.Add(Format(gx(x), "0.00000"))

ListBox8.Items.Add(Format(gy(y), "0.00000"))

Loop

L = Lam(x, y)

ListBox6.Items.Add(Format(L, "0.00000"))

xmin = x

ymin = y

End Sub

Sub vvod(ByVal t As TextBox, ByRef z As Double)

z = Val(t.Text)

End Sub

Sub vivod(ByVal z As Double, ByRef t As TextBox)

t.Text = CStr(z)

End Sub

Private Sub Button1_Click(ByVal sender As Object, ByVal e As EventArgs) Handles Button1.Click

Dim x, y, eps, xmin, ymin As Double

ListBox1.Items.Clear() : ListBox2.Items.Clear() : ListBox3.Items.Clear() : ListBox4.Items.Clear() : ListBox5.Items.Clear()

ListBox6.Items.Clear() : ListBox7.Items.Clear() : ListBox8.Items.Clear()

vvod(TextBox1, x)

vvod(TextBox2, y)

vvod(TextBox3, eps)

MO(x, y, eps, xmin, ymin)

vivod(xmin, TextBox4)

vivod(ymin, TextBox5)

End Sub

Private Sub Button2_Click(sender As System.Object, e As System.EventArgs) Handles Button2.Click

End

End Sub

End Class

Результат решения задачи оптимизации градиентным методом наискорейшего спуска (НСА):

С погрешность 0.1

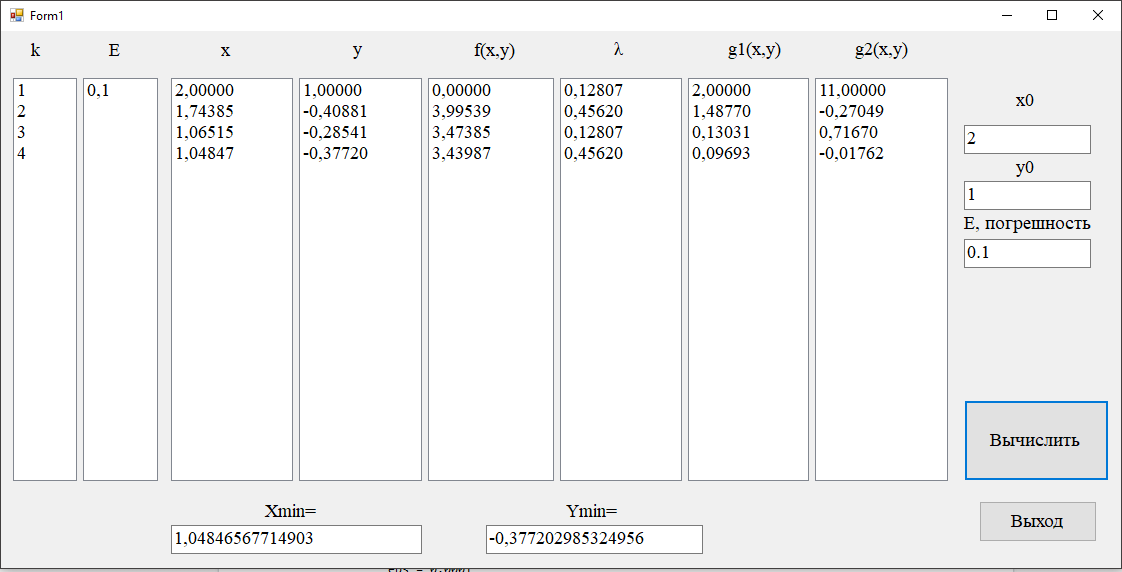
С погрешность 0.05

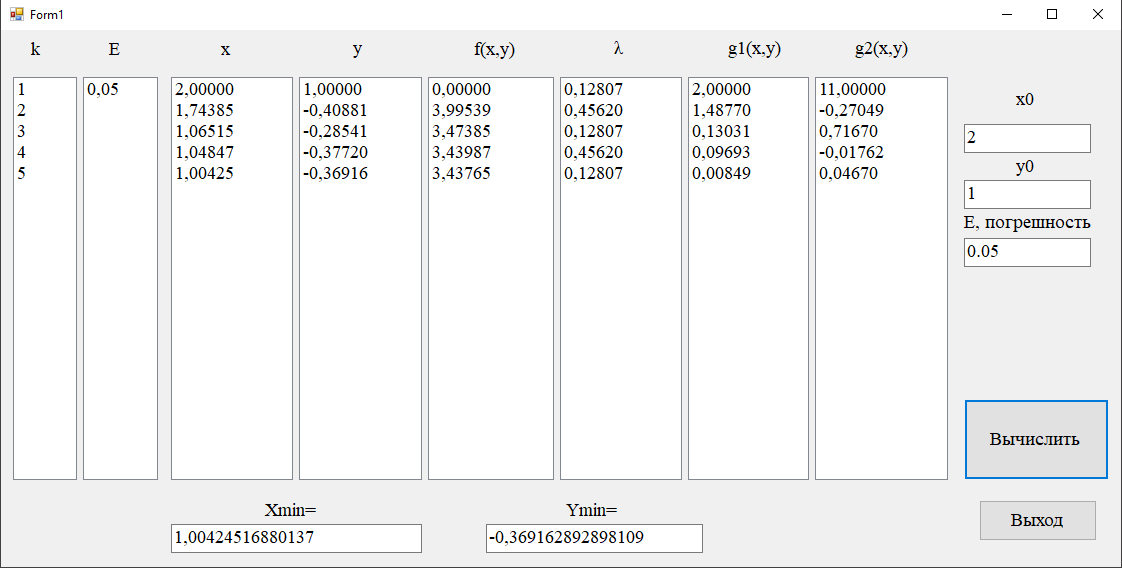
С погрешность 0.01

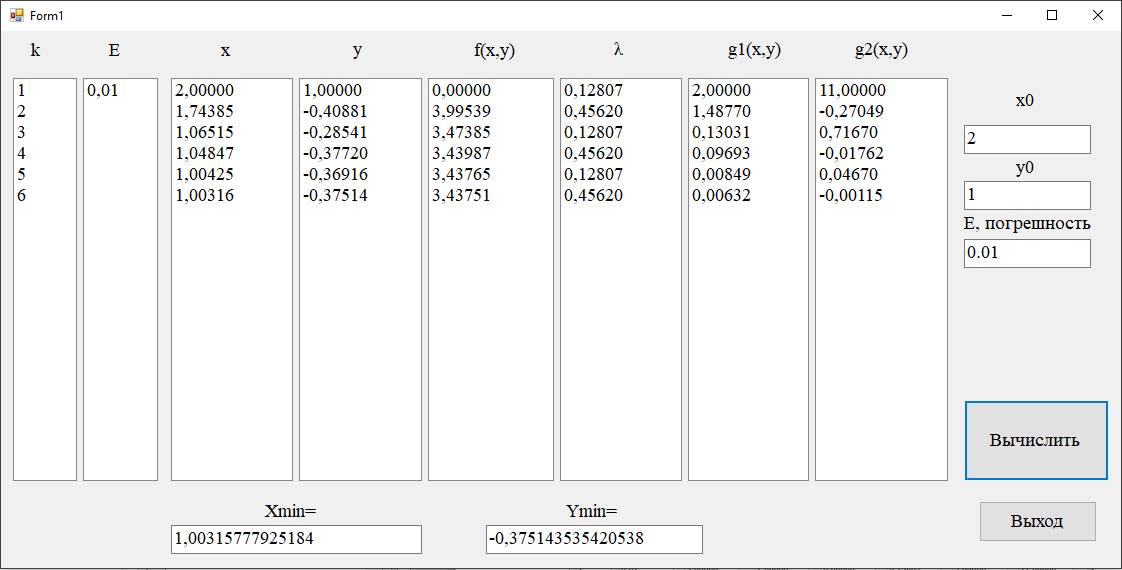
С погрешность 0.001

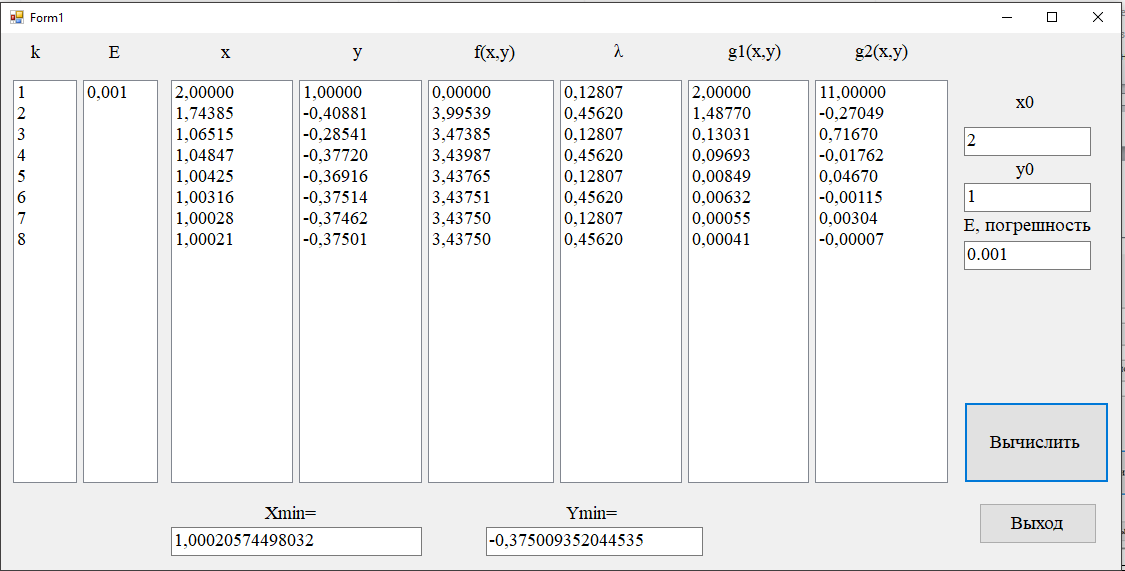
Метод	E	K	X	Y	F(X,Y)
НСА	0.1	3	1.04847	-0.37720	3.43987
	0.05	4	1.0425	-0.36916	3.43765
	0.01	5	1.00316	-0.37514	3.43751
	0.001	7	1.00021	-0.37501	3.43750

9) Траектория поиска минимума: