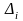4 Лаборторная работа ЧМ
.docxФедеральное агентство связи Ордена
Трудового Красного Знамени
федеральное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
(МТУСИ)
Кафедра Информатики
Предмет: Вычислительные модели
Лабораторная работа № 4
Тема:
««Методы решения обыкновенных дифференциальных уравнений»
Вариант 00
Выполнил:
Проверил(а): Величайший преподаватель
_________________
Москва 0000
Вариант
№ вар |
Уравнение |
x0 |
y0 |
h0 |
a |
b |
18 |
y' = y (x – 1) |
0 |
1 |
0.4 |
0 |
4 |
дифференциальное уравнение y' = y (x – 1)
интервал [0; 4];
начальные условия x0=0, y0=1;
шаг интегрирования h0=0.4.
Точное аналитическое решение заданного дифференциального уравнения
Найдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x)) методом разделения переменных. Для этого запишем уравнение в виде и проинтегрируем с учетом начальных условий
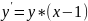
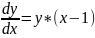
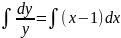
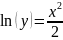 +
x + C
+
x + C
y=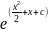
c=ln(1)+(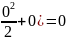
Получаем аналитическое решение уравнения
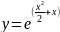
Значения точного решения ОДУ - y(x)
Вычислим значения полученного решения y(xi) на отрезке [0;4] с шагом изменения аргумента h=0.4:
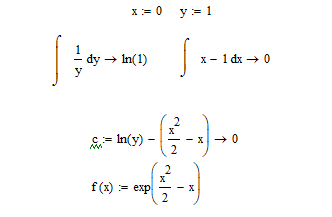
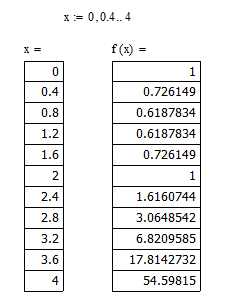
Численное решение заданного ДУ методом Эйлера
Найдем
значения численного решение ОДУ методом
Эйлера (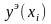 )
в точках
отрезка [0;4]
с шагом
h=0.4.
Для этого ДУ записывают в виде y’=f(x,y)
. Тогда общая формула для определения
очередного значения функции по методу
Эйлера имеет вид yi+1=yi+h×f(xi,yi),
где
)
в точках
отрезка [0;4]
с шагом
h=0.4.
Для этого ДУ записывают в виде y’=f(x,y)
. Тогда общая формула для определения
очередного значения функции по методу
Эйлера имеет вид yi+1=yi+h×f(xi,yi),
где
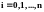 ,
,
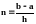 :
:
Значения
погрешностей:
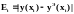
Вычислим
значения погрешностей
для
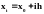 ,
,
:
,
,
:

Решения, полученные по составленной программе «расчетом на ПК»
Выполним
программу и получим решение (то есть
получим значения
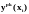 с шагом h=
0.4 и Е
=10-4
):
с шагом h=
0.4 и Е
=10-4
):
Схема Алгоритмов проекта
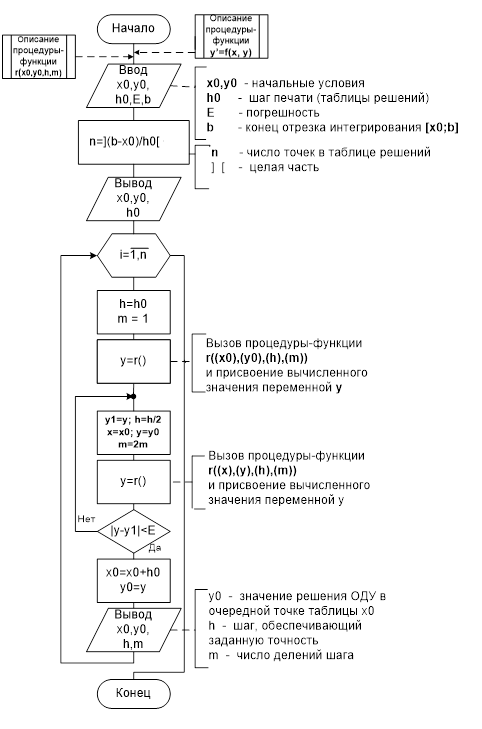
Рисунок 1 - Схема Алгоритмов проекта
Программный код
Option Strict On
Option Explicit On
Imports System.Math
Public Class Form1
Function fy(ByVal x As Double, ByVal y As Double) As Double
Dim z As Double
z = y * (x - 1)
Return z
End Function
Function r(ByVal x As Double, ByVal y As Double, ByVal h As Double, ByVal m As Double) As Double
Dim k1, k2, k3, k4 As Double
For j = 1 To m
k1 = fy(x, y)
k2 = fy(x + h / 2, y + h * k1 / 2)
k3 = fy(x + h / 2, y + h * k2 / 2)
k4 = fy(x + h, y + h * k3)
y = y + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)
x = x + h
Next
Return y
End Function
Sub diff(ByVal x0 As Double, ByVal y0 As Double, ByVal b As Double, ByVal h0 As Double, ByVal eps As Double)
Dim h, y, y1, x As Double
Dim n As Integer
Dim m As Integer
n = CInt((b - x0) / h0)
ListBox1.Items.Add(x0) : ListBox1.Items.Add(vbNewLine)
ListBox2.Items.Add(y0) : ListBox2.Items.Add(vbNewLine)
ListBox4.Items.Add(h0) : ListBox4.Items.Add(vbNewLine)
ListBox5.Items.Add(vbNewLine) : ListBox5.Items.Add(vbNewLine)
For i = 1 To n
h = h0
m = 1
y = r(x0, y0, h, m)
Do
y1 = y : h = h / 2
x = x0 : y = y0
m = 2 * m
y = r(x, y, h, m)
Loop Until Abs(y - y1) / 15 < eps
x0 = x0 + h0
y0 = y
ListBox1.Items.Add(Format(x0, "0.0"))
ListBox2.Items.Add(Format(y0, "0.000000000000000"))
ListBox4.Items.Add(h)
ListBox5.Items.Add(m)
Next
End Sub
Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click
Dim x0, y0, b, h0, eps As Double
x0 = Val(TextBox1.Text)
y0 = Val(TextBox2.Text)
b = Val(TextBox3.Text)
h0 = Val(TextBox4.Text)
eps = Val(TextBox5.Text)
diff(x0, y0, b, h0, eps)
End Sub
Private Sub Button2_Click(sender As System.Object, e As System.EventArgs) Handles Button2.Click
End
End Sub
End Class
Результат выполнения программы
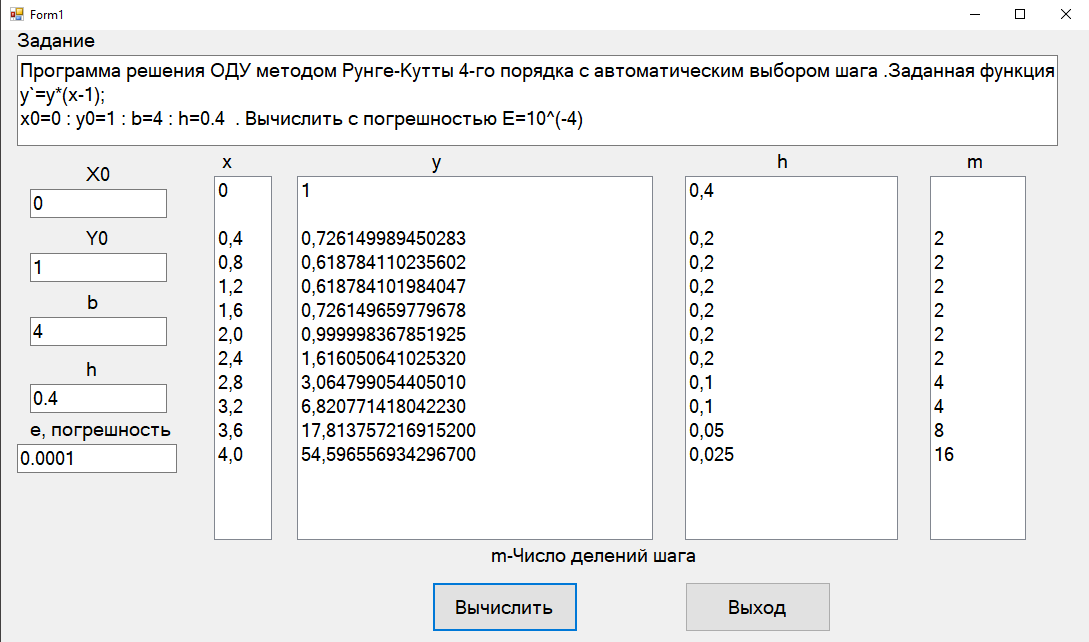
Рисунок 2 - Результат выполнения программы
Все решения, полученные выше, сведем в табл. результатов
xi |
y(xi) |
|
Ei |
|
|
0 |
1 |
1 |
0 |
1 |
0 |
0.4 |
0.72615 |
0.6 |
0.12615 |
0.7261499 |
10e-8 |
0.8 |
0.61878 |
0.456 |
0.16278 |
0.61878411 |
4.11e-6 |
1.2 |
0.61878 |
0.41952 |
0.19926 |
0.61878410 |
4.1e-6 |
1.6 |
0.72615 |
0.45308 |
0.27307 |
0.7261496 |
4e-7 |
2 |
1 |
0.56182 |
0.43818 |
0.999998 |
2e-6 |
2.4 |
1.61607 |
0.78655 |
0.82952 |
1.61605064 |
1.936e-5 |
2.8 |
3.06485 |
1.22702 |
1.83784 |
3.06479905 |
5.095e-5 |
3.2 |
6.82096 |
2.11047 |
4.71049 |
6.820771418 |
1.886e-4 |
3.6 |
17.81427 |
3.96768 |
13.84659 |
17.81375721 |
5.128e-4 |
4 |
54.59815 |
8.094075 |
46.5040753 |
54.59655693429 |
1.593e-3 |
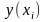 –
аналитическое решение ОДУ,
–
аналитическое решение ОДУ,
- решение ОДУ, полученное методом Эйлера,
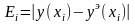 ,
,
- решение ОДУ методом Рунге-Кутты 4-го порядка,
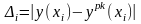
Графическая иллюстрация решений
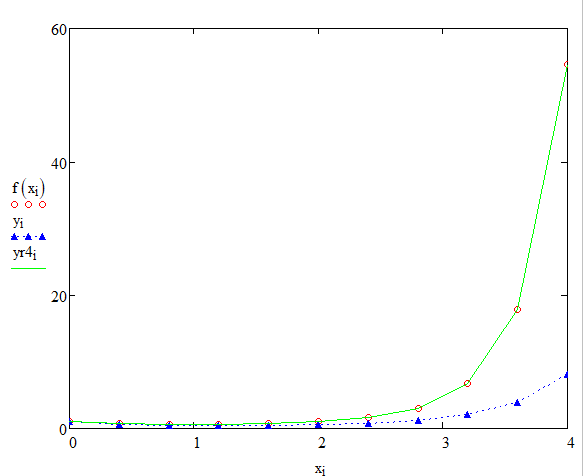
Рисунок 3 - Графическая иллюстрация решений