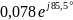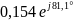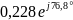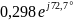- •1 Цель работы
- •2 Задание для лабораторной работы
- •3 Предварительный расчет
- •4. Машинный эксперимент
- •4.1. Исследование модуля и фазы комплексного сопротивления с-цепи.
- •4.2. Исследование модуля и фазы комплексного сопротивления rс-цепи.
- •4.3. Исследование модуля и фазы комплексного напряжения на конденсаторе rc-цепи.
- •4.4. Исследование модуля и фазы комплексного сопротивления l-цепи.
- •4.5. Исследование модуля и фазы комплексного сопротивления rl-цепи.
- •4.6. Исследование модуля и фазы комплексного напряжения на катушке rl-цепи.
- •Выводы.
- •Вопросы для самопроверки
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации Ордена трудового красного знамени федеральное государственное
бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра
Теория электрических цепей
Лабораторная работа №32
«Исследование пассивных цепей при гармоническом воздействии на постоянной частоте»
Выполнил студент
Группы БСТ
Фамилия И.О.
Проверил доц. Микиртичан А.Г.
Оглавление
1 Цель работы 3
2 Задание для лабораторной работы 3
3 Предварительный расчет 3
4. Машинный эксперимент 10
4.1. Исследование модуля и фазы комплексного сопротивления С-цепи. 10
4.2. Исследование модуля и фазы комплексного сопротивления RС-цепи. 13
4.3. Исследование модуля и фазы комплексного напряжения на конденсаторе RC-цепи. 14
4.4. Исследование модуля и фазы комплексного сопротивления L-цепи. 15
4.5. Исследование модуля и фазы комплексного сопротивления RL-цепи. 17
4.6. Исследование модуля и фазы комплексного напряжения на катушке RL-цепи. 18
Выводы. 19
Вопросы для самопроверки 21
1 Цель работы
С помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
2 Задание для лабораторной работы
Изучить основные положения ТЭЦ о частотных характеристиках электрических цепей, о комплексных сопротивлениях RC- и RL-цепей. Познакомится с возможностями схемотехнического моделирования. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
3.1.
Расчет в алгебраической форме комплексного
сопротивления конденсатора
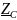 (рис.1), определение его полного
сопротивления
(рис.1), определение его полного
сопротивления
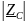 и аргумента arg
на пяти частотах 1, 2, 3, 4 и 5 кГц, если С =
32 нФ.
и аргумента arg
на пяти частотах 1, 2, 3, 4 и 5 кГц, если С =
32 нФ.
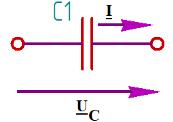
Рис.1
Формулы для расчета:
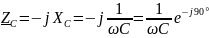 – комплексное сопротивление конденсатора;
– комплексное сопротивление конденсатора;
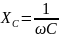 – емкостное сопротивление конденсатора;
– емкостное сопротивление конденсатора;
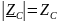 – модуль комплексного сопротивления
конденсатора;
– модуль комплексного сопротивления
конденсатора;
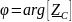 – аргумент (фаза) комплексного
сопротивления конденсатора;
– аргумент (фаза) комплексного
сопротивления конденсатора;
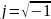 -
мнимая единица;
-
мнимая единица;
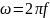 – угловая частота;
– угловая частота;
f – частота.
Полученные величины занесли в таблицу 1 предварительного расчета.
Таблица 1 – Расчет сопротивления конденсатора
По предварительному расчету |
Получено экспериментально |
||||||
f, кГц |
С, нФ |
|
|
|
Ом |
град. |
|
1 |
32 |
-j4974 |
4974 |
-90 |
4974 |
-90 |
|
2 |
32 |
-j2487 |
2487 |
-90 |
2487 |
-90 |
|
3 |
32 |
-j1658 |
1658 |
-90 |
1658 |
-90 |
|
4 |
32 |
-j1243 |
1243 |
-90 |
1243 |
-90 |
|
5 |
32 |
-j994,72 |
994,72 |
-90 |
994,724 |
-90 |
|
Векторная диаграмма показана на рис. 2.

Рис.2
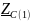 - сопротивление конденсатора на частоте
f = 1 кГц,
- сопротивление конденсатора на частоте
f = 1 кГц,
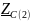 - сопротивление конденсатора на частоте
f = 2 кГц,
- сопротивление конденсатора на частоте
f = 2 кГц,
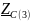 - сопротивление конденсатора на частоте
f = 3 кГц,
- сопротивление конденсатора на частоте
f = 3 кГц,
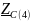 - сопротивление конденсатора на частоте
f = 4кГц,
- сопротивление конденсатора на частоте
f = 4кГц,
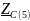 - сопротивление конденсатора на частоте
f = 5 кГц.
- сопротивление конденсатора на частоте
f = 5 кГц.
3.2.
Расчет в алгебраической форме комплексного
сопротивления
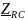 RC-цепи (рис.3) для пяти
частот 1, 2, 3, 4, 5 кГц. Определение его
полного сопротивления и аргумента, если
R = 2500 Ом, С = 32 нФ.
RC-цепи (рис.3) для пяти
частот 1, 2, 3, 4, 5 кГц. Определение его
полного сопротивления и аргумента, если
R = 2500 Ом, С = 32 нФ.
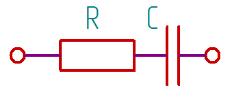
Рис.3
Формулы для расчета:
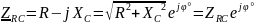 – комплексное сопротивление RC-цепи;
– комплексное сопротивление RC-цепи;
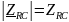 – модуль комплексного сопротивления
двухполюсника;
– модуль комплексного сопротивления
двухполюсника;
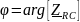 – аргумент (фаза) комплексного
сопротивления двухполюсника;
– аргумент (фаза) комплексного
сопротивления двухполюсника;
- мнимая единица;
– угловая частота;
f – частота.
Полученные величины занесли в таблицу 2.
Таблица 2 – Расчет полного сопротивления RC-цепи
По предварительному расчету |
Получено экспериментально |
||||||
f, кГц |
С, нФ |
R, кОм |
|
|
|
Ом |
град. |
1 |
32 |
2,5 |
2500-j4974 |
5567 |
-63,3 |
5567 |
-63,3 |
2 |
32 |
2,5 |
2500-j2487 |
3526 |
-44,9 |
3526 |
-44,9 |
3 |
32 |
2,5 |
2500-j1658 |
3000 |
-33,6 |
3000 |
-33,6 |
4 |
32 |
2,5 |
2500-j1243 |
2792 |
-26,4 |
2792 |
-26,4 |
5 |
32 |
2,5 |
2500-j994,72 |
2691 |
-21,7 |
2691 |
-21,7 |
Векторная диаграмма показана на рис.4.
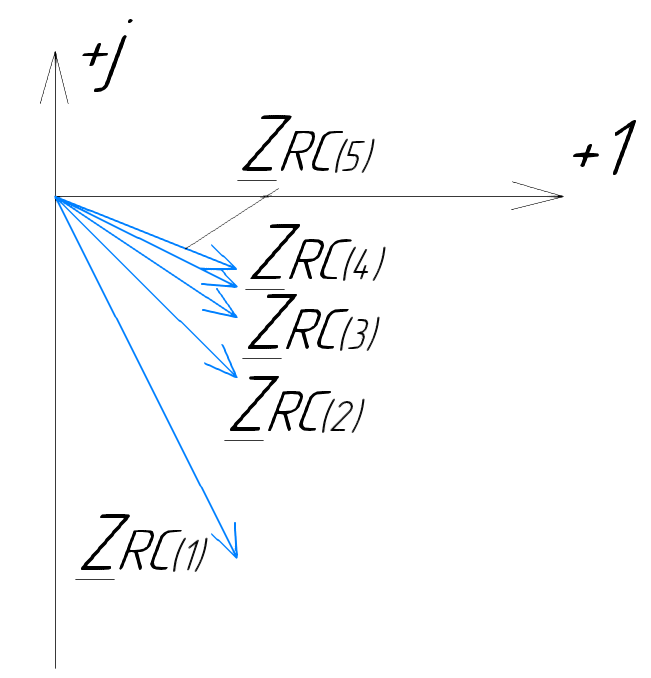
Рис.4
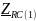 - комплексное сопротивление RC-цепи
на частоте f = 1 кГц,
- комплексное сопротивление RC-цепи
на частоте f = 1 кГц,
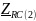 -
комплексное сопротивление RC-цепи
на частоте f = 2 кГц,
-
комплексное сопротивление RC-цепи
на частоте f = 2 кГц,
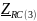 - комплексное сопротивление RC-цепи
на частоте f = 3 кГц,
- комплексное сопротивление RC-цепи
на частоте f = 3 кГц,
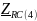 - комплексное сопротивление RC-цепи
на частоте f = 4кГц,
- комплексное сопротивление RC-цепи
на частоте f = 4кГц,
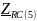 - комплексное сопротивление RC-цепи
на частоте f = 5 кГц.
- комплексное сопротивление RC-цепи
на частоте f = 5 кГц.
3.3.
Расчет напряжения на конденсаторе
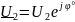 ,
если
,
если
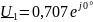 на частотах 1, 2, 3, 4, 5 кГц, определение
его модуля и фазы (рис.5).
на частотах 1, 2, 3, 4, 5 кГц, определение
его модуля и фазы (рис.5).
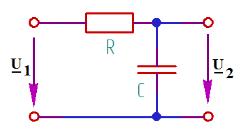
Рис.5
Формулы для расчета:
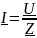 –
комплексный ток;
–
комплексный ток;
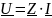 – комплексное падение напряжения;
– комплексное падение напряжения;
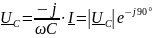 - комплексное напряжение на конденсаторе.
- комплексное напряжение на конденсаторе.
Полученные данные занесли в таблицу 3.
Таблица 3 – Расчет напряжения на конденсаторе
По предварительному расчету |
Получено экспериментально |
||||||||
f, кГц |
С, нФ |
R, кОм |
U1, В |
U2, В |
φ, град. |
|
U2, В |
φ, град. |
|
1 |
32 |
2,5 |
0,707 |
0,893 |
-26,7 |
|
0,893 |
-26,7 |
|
2 |
32 |
2,5 |
0,707 |
0,705 |
-45,2 |
|
0,705 |
-45,2 |
|
3 |
32 |
2,5 |
0,707 |
0,553 |
-56,5 |
|
0,553 |
-56,5 |
|
4 |
32 |
2,5 |
0,707 |
0,445 |
-63,6 |
|
0,445 |
-63,6 |
|
5 |
32 |
2,5 |
0,707 |
0,37 |
-68,3 |
|
0,37 |
-68,3 |
|
3.4.
Расчет в экспоненциальной форме
комплексного сопротивления катушки
индуктивности
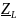 (рис.6) для пяти частот 1, 2, 3, 4, 5 кГц.
Определение ее полного сопротивления
и аргумента, если L = 31 мГн.
(рис.6) для пяти частот 1, 2, 3, 4, 5 кГц.
Определение ее полного сопротивления
и аргумента, если L = 31 мГн.
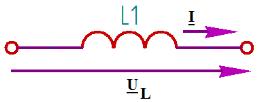
Рис.6
Формулы для расчета:
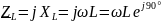 – комплексное сопротивление катушки;
– комплексное сопротивление катушки;
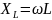 – индуктивное сопротивление катушки;
– индуктивное сопротивление катушки;
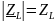 – модуль комплексного сопротивления
катушки;
– модуль комплексного сопротивления
катушки;
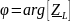 – аргумент (фаза) комплексного
сопротивления катушки;
– аргумент (фаза) комплексного
сопротивления катушки;
- мнимая единица;
– угловая частота;
f – частота.
Полученные данные занесли в таблицу 4.
Таблица 4 – Расчет сопротивления катушки индуктивности
По предварительному расчету |
Получено экспериментально |
||||||
f, кГц |
L, мГн |
|
|
|
Ом |
град. |
|
1 |
31 |
j194,779 |
194,779 |
90 |
194,779 |
90 |
|
2 |
31 |
j389,557 |
389,557 |
90 |
389,557 |
90 |
|
3 |
31 |
j584,336 |
584,336 |
90 |
584,336 |
90 |
|
4 |
31 |
j779,115 |
779,115 |
90 |
779,115 |
90 |
|
5 |
31 |
j973,894 |
973,894 |
90 |
973,894 |
90 |
|
Векторная диаграмма (рис.7).
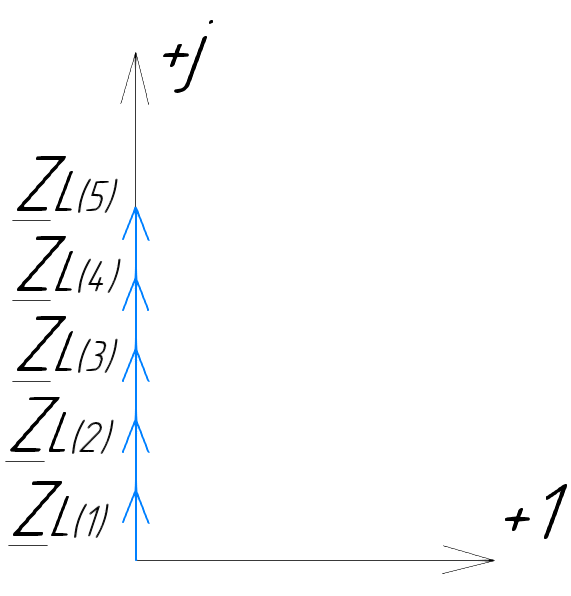
Рис.7
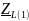 - комплексное сопротивление катушки на
частоте f = 1 кГц,
- комплексное сопротивление катушки на
частоте f = 1 кГц,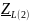 - комплексное сопротивление катушки
на частоте f = 2 кГц,
- комплексное сопротивление катушки
на частоте f = 2 кГц,
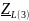 - комплексное сопротивление катушки
на частоте f = 3 кГц,
- комплексное сопротивление катушки
на частоте f = 3 кГц,
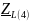 - комплексное сопротивление катушки
на частоте f = 4кГц,
- комплексное сопротивление катушки
на частоте f = 4кГц,
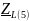 - комплексное сопротивление катушки
на частоте f = 5 кГц.
- комплексное сопротивление катушки
на частоте f = 5 кГц.
3.5.
Расчет в алгебраической форме комплексного
сопротивления
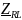 RL-цепи (рис.8) для пяти
частот 1, 2, 3, 4, 5 кГц. Определение его
полного сопротивления и аргумента, если
R = 2500 Ом, L
= 31 мГн.
RL-цепи (рис.8) для пяти
частот 1, 2, 3, 4, 5 кГц. Определение его
полного сопротивления и аргумента, если
R = 2500 Ом, L
= 31 мГн.

Рис.8
Формулы для расчета:
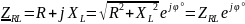 – комплексное сопротивление RL-цепи;
– комплексное сопротивление RL-цепи;
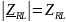 – модуль комплексного сопротивления
двухполюсника;
– модуль комплексного сопротивления
двухполюсника;
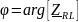 – аргумент (фаза) комплексного
сопротивления двухполюсника;
– аргумент (фаза) комплексного
сопротивления двухполюсника;
- мнимая единица;
– угловая частота;
f – частота.
Полученные данные занесли в таблицу 5.
Таблица 5 – Расчет полного сопротивления RL-цепи
По предварительному расчету |
Получено экспериментально |
|||||||
f, кГц |
L, мГн |
R, кОм |
|
|
|
Ом |
град. |
|
1 |
31 |
2,5 |
2500+j194,779 |
2508 |
4,5 |
2508 |
4,5 |
|
2 |
31 |
2,5 |
2500+j389,557 |
2530 |
8,9 |
2530 |
8,9 |
|
3 |
31 |
2,5 |
2500+j584,336 |
2567 |
13,2 |
2567 |
13,2 |
|
4 |
31 |
2,5 |
2500+j779,115 |
2619 |
17,3 |
2619 |
17,3 |
|
5 |
31 |
2,5 |
2500+j973,894 |
2683 |
21,3 |
2683 |
21,3 |
|
Векторная диаграмма показана на рис.9.
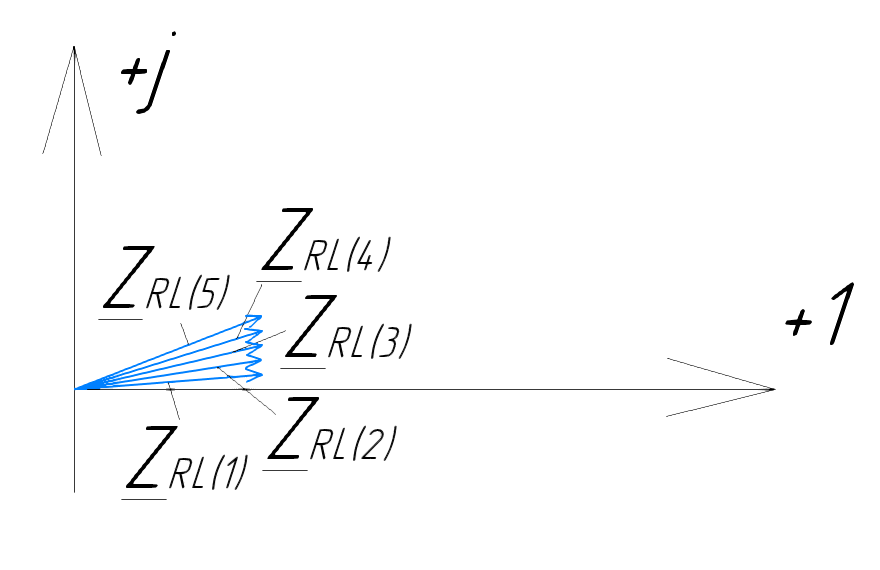
Рис.9
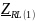 - комплексное сопротивление RL-цепи
на частоте f = 1 кГц,
- комплексное сопротивление RL-цепи
на частоте f = 1 кГц,
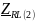 - комплексное сопротивление RL-цепи
на частоте f = 2 кГц,
- комплексное сопротивление RL-цепи
на частоте f = 2 кГц,
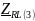 - комплексное сопротивление RL-цепи
на частоте f = 3 кГц,
- комплексное сопротивление RL-цепи
на частоте f = 3 кГц,
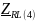 - комплексное сопротивление RL-цепи
на частоте f = 4кГц,
- комплексное сопротивление RL-цепи
на частоте f = 4кГц,
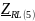 - комплексное сопротивление RL-цепи
на частоте f = 5 кГц.
- комплексное сопротивление RL-цепи
на частоте f = 5 кГц.
3.6. Расчет напряжения на катушке индуктивности , если для пяти частот 1, 2, 3, 4, 5 кГц, определение его модуля и фазы (рис.10).
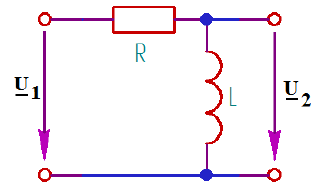
Рис. 10
Полученные данные занесли в таблицу 6.
Таблица 6 – Расчет напряжения на катушке индуктивности
По предварительному расчету |
Получено экспериментально |
||||||||
f, кГц |
L, мГн |
R, кОм |
U1, В |
U2, В |
φ, град. |
, В |
U2, В |
φ, град. |
|
1 |
31 |
2,5 |
0,707 |
0,078 |
85,5 |
|
0,078 |
85,5 |
|
2 |
31 |
2,5 |
0,707 |
0,154 |
81,1 |
|
0,154 |
81,1 |
|
3 |
31 |
2,5 |
0,707 |
0,228 |
76,8 |
|
0,228 |
76,8 |
|
4 |
31 |
2,5 |
0,707 |
0,298 |
72,7 |
|
0,298 |
72,7 |
|
5 |
31 |
2,5 |
0,707 |
0,363 |
68,7 |
|
0,363 |
68,7 |
|

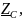 Ом
Ом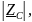 Ом
Ом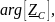 град.
град.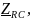 Ом
Ом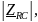 Ом
Ом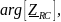 град.
град.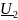 ,
В
,
В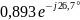
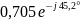
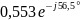
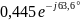
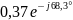
 Ом
Ом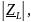 Ом
Ом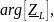 град.
град.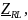 Ом
Ом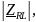 Ом
Ом град.
град.