
- •1. Квантовая механика и физика атома
- •2. Элементы статистической физики и термодинамики.
- •1. Колебания.
- •2. Волны.
- •Вопросы для подготовки к экзамену По разделу «Элементы квантовой и статистической физики» Квантовая физика и физика атома.
- •Статистическая физика и термодинамика.
- •Основные физические постоянные (округленные значения)
- •Плотность твердых тел
- •Массы атомов легких изотопов
- •Масса и энергия покоя некоторых частиц
ВВЕДЕНИЕ
Дисциплина «Физика», входит в базовую часть цикла общих математических и естественнонаучных дисциплин в государственных образовательных стандартах. Она служит для ознакомления студентов с современной физической картиной мира, для приобретения навыков экспериментального исследования физических явлений и процессов, для изучения теоретических методов анализа физических явлений, а также для обучения грамотному применению положений фундаментальной физики к научному анализу ситуаций, с которыми бакалавру придется сталкиваться при создании новых технологий. Кроме того, она способствует выработке у студентов основ естественнонаучного мировоззрения и ознакомления с историей развития физики и основных её открытий.
Цели и задачи освоения дисциплины «Физика», компетенции, которыми студент должен обладать в результате освоения дисциплины, подробно разобраны в Части 1 настоящего УМП.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Работа студента-заочника по изучению курса физики складывается из следующих видов работ: самостоятельного изучения физики по учебным пособиям, работы в контакте с преподавателями кафедры физики, решения задач, выполнения контрольных и лабораторных работ, сдачи зачетов и экзаменов.
Самостоятельное изучение курса физики по учебным пособиям
Самостоятельная работа с учебными пособиями является главным видом работы студента-заочника. Здесь нужно иметь ввиду:
I. Изучать курс физики необходимо систематически в течение всего учебного процесса. Изучение физики в сжатые сроки перед экзаменом не даст глубоких и прочных знаний.
2. В качестве учебного пособия студенты могут использовать один из учебников, указанных в списке основной литературы. Кроме того, рекомендуется использовать конспекты лекций, имеющиеся по всем изучаемым разделам курса в Центре дистанционного обучения. В этих лекциях доступно и достаточно строго изложены все вопросы изучаемого курса физики.
3. При чтении учебного пособия желательно составлять конспект, в котором записывать законы и формулы, выражающие эти законы, определения физических величин и единиц их измерения, делать чертежи и решать типовые задачи.
4. Самостоятельную работу по изучению курса физики рекомендуется подвергать систематическому самоконтролю. Для этого после изучения очередного раздела курса следует ответить на контрольные вопросы, предназначенные для подготовки к экзамену.
Решение задач
Систематическое решение задач - необходимое условие успешного изучения курса физики. Решение задач помогает уяснить смысл физических законов, закрепляет в памяти формулы, прививает навыки практического применения теоретических знаний. При решении задачи рекомендуется следующее:
I. После слова "дано" выписать все величины с их числовыми значениями, которые будут использованы в процессе решения задачи. Числовые значения, исключая те случаи, когда определяются безразмерные отношения, тут же переводить в систему СИ, проставляя рядом соответствующие наименования. После слова "найти" выписать все искомые величины .
2. Указать те основные законы и формулы, на которых базируется решение данной задачи, и привести их словесную формулировку. Разъяснить смысл буквенных обозначений, входящих в исходную формулу. Если такая формула является частным случаем фундаментального закона, то ее необходимо вывести из этого закона.
3. Сделать чертеж или график, поясняющий содержание задачи (в тех случаях, когда это возможно). Выполнить его надо аккуратно, при помощи карандаша, циркуля, линейки, лекал. На чертеже или графике чернилами должны быть нанесены обозначения всех буквенных величин, которые используются в расчетных формулах и могут быть пояснены чертежом.
4. Каждый этап решения задачи сопровождать краткими. но исчерпывающими пояснениями.
5. Физические задачи весьма разнообразны, и дать единый рецепт их решения невозможно. Однако, как правило, физические задачи следует решать в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи, и взятых из таблицы. При этом способе не производятся вычисления промежуточных величин; числовые значения подставляются только в окончательную (рабочую) формулу, выражающую искомую величину. Рабочая формула должна быть записана в рационализованной форме, все величины, входящие в нее, выражены в единицах СИ.
6. Подставить в рабочую формулу наименования единиц (в которых выражены заданные числовые значения) и, путем упрощающих действий с ними, убедиться в правильности наименования искомой величины.
7. Подставить в рабочую формулу числовые значения, выраженные в единицах одной системы, рекомендуется - в СИ. Несоблюдение этого правила приводит к неверному результату. Исключение из этого правила допускается лишь для тех однородных величин, которые входят в виде сомножителей в числитель и знаменатель формулы с одинаковыми показателями степени. Такие величины можно выразить в любых единицах, но обязательно в одинаковых.
8. Произвести расчетные действия с величинами, подставленными в рабочую формулу, записать в ответе числовое значение и сокращенное наименование единиц измерения искомой величины.
9. При подстановке в рабочую формулу, а также при выражении ответа числовые значения величин записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на десять в соответствующей степени. Например, вместо 3520 надо записать 3,52.103 вместо 0,00129 записать 1,29.10-3 и т.д. Рекомендуемая запись числовых значений облегчает расчетные действия с ними, является более компактной и наглядной.
10. Оценить правдоподобность числового ответа. В ряде случаев такая оценка помогает своевременно обнаружить ошибочность полученного результата и устранить ее. Например, коэффициент полезного действия тепловой машины не может быть больше единицы, электрический заряд не бывает меньше электронного заряда е = 1,6.10-19 Кл, скорость тела не может превзойти скорость света в вакууме с = 3.108 м/с и т.д.
Чтобы приобрести необходимые навыки в решении задач и подготовиться к выполнению контрольной работы, следует после изучения очередного раздела курса физики внимательно разобрать помещенные ниже примеры решения типовых задач.
Выполнение контрольных работ
Студенты МТУСИ направлений 15.03.04. «Автоматизация технологических процессов и производств» и 09.03.02. «Информационные системы и технологии» 2 курса выполняют контрольную работу № 2 по разделам «Колебания и волны»; «Элементы квантовой и статистической физики».
При выполнении контрольной работы студенту необходимо руководствоваться следующим:
I. Все контрольные работы выполняются только по условиям задач данного пособия. Замена какой-либо контрольной работы другой, взятой из аналогичного пособия, но другого года издания, не допускается.
2. Контрольные работы выполняются в обычной школьной тетради в клетку, на первой странице которой наклеивается специальный бланк, выдаваемый деканатом.
3. Контрольная работа выполняется чернилами темного цвета (черного или синего). Для замечаний преподавателя на страницах тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью без сокращений. Задачи нумеруются теми же номерами, которые указаны в контрольном задании.
4. Решение задач выполняется в соответствии с правилами, изложенными в разделе "Решение задач" (см. с. 5-6). В задачах, отмеченных звездочкой, необходимо сделать поясняющий чертеж или график.
5. После получения из института прорецензированной работы студент обязан выполнить все указания рецензента.
6. Если контрольная работа после рецензирования не зачтена, студент представляет ее на повторную рецензию, исправив решения тех задач, которые оказались выполненными неверно. При этом все исправления, дополнения, повторные решения задач, вытекающие из требований рецензента, выполняются в этой же тетради на свободных страницах. Нельзя делать исправления в том же месте, где допущены ошибки. Если исправления выполняются в отдельной тетради, то эта тетрадь обязательно представляется вместе с не зачтенной работой.
8. Если контрольная работа зачтена, но рецензентом указано на необходимость внести какие-либо дополнения, пояснения или исправления в решения задач, то все они должны быть выполнены до экзамена (зачета).
9. При получении экзаменационного билета экзаменатору предъявляется зачтенная работа. Студент должен быть готов дать во время экзамена пояснения по существу решения задач, входящих в его контрольную работу.
10. Срок действия зачтенных контрольных работ, по тематике которых не сдан экзамен - два года.
Сдача зачетов и экзаменов
К сдаче зачета или экзамена допускаются студенты, выполнившие установленное число контрольных и лабораторных работ. Контрольные работы, зачтенные рецензентом с подписью преподавателя, проверившего исправления, предъявляются экзаменатору.
При сдаче экзамена или зачета студент должен обнаружить знание курса физики в объеме, установленном программой, и умение решать физические задачи, а также готовность дать пояснения по существу решений задач, входящих в его контрольные работы.
В соответствии с учебным планом студенты МТУСИ направлений 15.03.04. «Автоматизация технологических процессов и производств» и 09.03.02. «Информационные системы и технологии» в конце первого семестра второго курса сдают экзамен по разделам «Колебания и волны», «Элементы квантовой и статистической физики».
Тестирование
Экзамен может проводиться в виде тестирования в компьютерном классе.
Обратите внимание на правила ввода данных при ответах на тестовые задания:
Все числа в ответах на вопросы в заданиях открытого типа (если иное не оговорено) представляются в стандартном виде
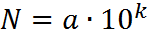 и записываются
с клавиатуры так:
и записываются
с клавиатуры так:  где
где  целая часть,
целая часть,
 дробная часть
числа
дробная часть
числа  Целая часть
числа
Целая часть
числа  отделяется
от дробной запятой. Например,
отделяется
от дробной запятой. Например,  записывается так: 3,1(-3). Если порядок
числа
записывается так: 3,1(-3). Если порядок
числа 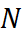 равен нулю,
то число записывается обычным образом
без указания
равен нулю,
то число записывается обычным образом
без указания  ,
например,
,
например, 
Запись формул по шаблону производится буквами латинского алфавита. При этом в шаблоне заполняется только та часть, которая представлена его элементами в описании. В тех случаях, когда шаблон составляет часть выражения, записывается все, что стоит в кавычках, например,
 , где
, где  ,
b
,
b .
Ответ: -
.
Ответ: -
Символ операции @, если он специально не определен в задании, может обозначать круглые скобки ( ), знаки сложения (+), вычитания (-), умножения (*), в том числе скалярного, векторного произведения (#), деления ( / ), возведения в
 степень (^
степень (^ ).
).
В некоторых заданиях без пояснения используются следующие обозначения: m – масса; k – коэффициент жесткости; I – момент инерции или сила тока; r – коэффициент силы (момента силы) сопротивления; C – емкость конденсатора; L – индуктивность катушки; R – сопротивление; Δ – логарифмический декремент; Q – добротность; Т – период;
 - коэффициент затухания;
- коэффициент затухания;  - круговая частота;
- круговая частота;  -частота;
-частота;  - фаза;
- фаза;  - длина волны;
- длина волны;  – электрическая и магнитная постоянные;
– электрическая и магнитная постоянные;
 - относительные диэлектрическая и
смещение; с
– скорость света в вакууме.магнитная
проницаемости; E,
H
– напряженности электрического и
магнитного полей; B,
D
– магнитная индукция и электрическое
- относительные диэлектрическая и
смещение; с
– скорость света в вакууме.магнитная
проницаемости; E,
H
– напряженности электрического и
магнитного полей; B,
D
– магнитная индукция и электрическое
СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО КУРСА
ВВЕДЕНИЕ
Изложение курса начинается с раздела "Колебания и волны". В раздел "Элементы квантовой и статистической физики" в качестве составных частей входят квантовая оптика, физика атома и физика твердого тела.
КОЛЕБАНИЯ И ВОЛНЫ
1. К о л е б а н и я (механические и электромагнитные)
Общая характеристика колебаний. Общие признаки колебательного движения, его характеристики и классификация. Примеры колебательных систем. Колебательные системы с одной степенью свободы: пружинный маятник, математический и физический маятники, контур Томсона.
Гармонические колебания. Общая характеристика. Дифференциальное уравнение гармонически колеблющихся систем и его решение. Определение периодов колебаний. Энергия гармонического колебательного движения.
Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Зависимость амплитуды от времени. Логарифмический декремент затухания. Частота затухающих колебаний. Апериодическое движение.
Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Резонанс и резонансная частота. Диаграмма колебаний. Переменный ток.
Сложение колебаний. Сложение одинаково направленных гармонических колебаний с равными и мало отличающимися частотами (биения). Сложение взаимно - перпендикулярных гармонических колебаний с равными и кратными частотами.
2. В о л н ы (упругие и электромагнитные).
Упругие волны. Волны в упругой среде, механизм их образования. Продольные и поперечные волны. Скорость распространения упругих волн. Уравнение плоской волны.
Электромагнитные волны. Волновое уравнение электромагнитной волны как решение уравнений Максвелла. Скорость распространения электромагнитных волн. Фазовая и групповая скорость. Перенос энергии волнами. Вектор Умова - Пойнтинга.
Элементы волновой теории света. Корпускулярная и волновая теории света. Принцип Гюйгенса и его применение для вывода законов отражения и преломления света. Полное внутреннее отражение.
Интерференция волн. Когерентные волны. Разность фаз и условия усиления и ослабления волн. Распределение энергии в интерференционных явлениях. Стоячие волны. Узлы и пучности. Особенности отражения волн на границе двух сред. Способы получения когерентных световых волн: щели Юнга, зеркала и бипризмы Френеля. Принцип суперпозиции волн. Интерференционная картина, образуемая двумя когерентными источниками света. Интерференция в тонких пленках. Геометрическая, оптическая и полная разность хода. Полосы равной толщины и равного наклона.
Дифракция света. Дифракция и условия ее наблюдения. Принцип Гюйгенса – Френеля. Метод зон Френеля. Прямолинейное распространение света. Дифракция света на одиночных отверстиях и экранах. Дифракция в параллельных лучах: щель и дифракционная решетка. Применение дифракционной решетки. Формула Брегга – Вульфа. Исследование структуры кристаллов.
Дисперсия света. Призматический и дифракционный спектры. Понятие электронной теории дисперсии. Нормальная и аномальная дисперсия.
Поляризация света. Естественный и поляризованный свет. Поляризация при отражении и преломлении. Закон Брюстера (без вывода). Двойное лучепреломление и его объяснение. Призма Николя. Закон Малюса. Поляроиды и их применение. Искусственная анизотропия. Эффект Керра.
Тепловое излучение. Тепловое излучение в классической физике среди других типов излучения. Равновесное излучение. Лучеиспускательная и поглощательная способности тел. Абсолютно черное тело. Закон Кирхгофа. Закон Стефана-Больцмана. Закон смещения Вина. Формула Планка. Связь между формулой Планка и законами Стефана-Больцмана и Вина. Оптическая пирометрия.
Давление света. Электромагнитное объяснение давления света. Связь давления света с интенсивностью волны.
ЭЛЕМЕНТЫ КВАНТОВОЙ И СТАТИСТИЧЕСКОЙ ФИЗИКИ
1. Квантовая механика и физика атома
Предпосылки квантовой физики. Трудности классической физики и корпускулярно - волновой дуализм. Несостоятельность классической теории атома. Экспериментальное обоснование квантовой теории. Фотоэффект и эффект Комптона. Дифракция электронов. Постулаты Бора и формула Планка. Формула де Бройля.
Элементы квантовой механики. Волновая функция де Бройля и её статистический смысл. Принцип суперпозиции состояний. Принцип неопределённости Гейзенберга. Стационарное уравнение Шредингера и его применение к свободному электрону. Потенциальные барьеры. Частица в "потенциальном ящике". Туннельный эффект. Квантовый осциллятор.
Физика атома. Квантование. Момент импульса. Спин электрона. Квантовые числа. Квантовая теория атома водорода. Энергетические уровни. Спектры излучения и испускания. Правила отбора.
Многоэлектронные атомы и молекулы. Распределение электронов в атоме. Принцип Паули. Электронные оболочки. Периодическая система элементов.
2. Элементы статистической физики и термодинамики.
Основные положения статистической физики. Степени свободы молекул. Распределение энергии по степеням свободы. Понятие о средних значениях физических величин и статистическое описание систем с большим числом частиц. Понятие функции распределения плотности вероятности. Максвелловское распределение молекул по скоростям, импульсам и энергии. Больцмановское распределение частиц в потенциальном поле.
Статистическая термодинамика. Понятие об обратимых и необратимых процессах. Микро- и макросостояние системы. Статистический вес. Адиабатический процесс и его уравнение. Первое начало термодинамики в статистической физике. Внутренняя энергия и энтропия. Теплоемкость тел. Второе и третье начала термодинамики.
Квантовая статистика. Тождественность квантовых частиц. Фермионы и бозоны. Понятие о функциях распределения Ферми-Дирака и Бозе-Эйнштейна. Энергия Ферми. Функция распределения Планка для фотонного газа. Формула Планка для плотности теплового излучения и её следствия.
Элементы зонной теории твердых тел. Принцип Паули и распределение электронов по энергетическим уровням в кристаллах (образование зон). Понятие о свободных электронах и дырках. Концентрация носителей в зоне проводимости и валентной зоне. Электропроводность металлов, полупроводников и диэлектриков. Ширина зоны проводимости и химический потенциал. Контактные явления и термоэмиссия. Теплоемкость твердых тел.
ЛИТЕРАТУРА
Основная
1. Иродов И.Е. Квантовая физика. Основные законы [Электронный ресурс]: учебное пособие/ Иродов И.Е.— Электрон. текстовые данные.— М.: БИНОМ. Лаборатория знаний, 2014.— 259 c.— Режим доступа: http://www.iprbookshop.ru/6551.— ЭБС «IPRbooks», по паролю
2. Иродов И.Е. Волновые процессы. Основные законы [Электронный ресурс]/ Иродов И.Е.— Электрон. текстовые данные.— М.: БИНОМ. Лаборатория знаний, 2015.— 264 c.— Режим доступа: http://www.iprbookshop.ru/6557.— ЭБС «IPRbooks», по паролю
3. Жилинский А.П., Егорова Т.С., Мискинова Н.А. Основы статистической физики и физики твердого тела. М., 2015.
Дополнительная
1. Иродов И.Е. Физика макросистем. Основные законы [Электронный ресурс]: учебное пособие/ Иродов И.Е.— Электрон. текстовые данные.— М.: БИНОМ. Лаборатория знаний, 2012.— 206 c.— Режим доступа: http://www.iprbookshop.ru/6582.— ЭБС «IPRbooks», по паролю
2. Трофимова Т.И. Курс физики. – М., ВШ, 2007.
3. Жилинский А.П., Наливайко В.П. Элементы квантовой физики: конспект лекций по курсу «Физика» / МТУСИ. 2010.
4. Жилинский А.П., Дегтярев В.Ф., Егорова Т.С, Самодурова И.Д. Волновые процессы. Конспект лекций, МТУСИ, 2004.
5.Методические указания для выполнения индивидуальных заданий по всем разделам курса физики. МТУСИ
6.Описания лабораторных работ. МТУСИ
Задачники
Чертов А.Г., Воробьев А. А., Федоров М.Ф. Задачник по физике,-М: Высшая школа, 1997.
Волькенштейн В.С. Сборник задач по общему курсу физики.- 1970 - 2002.
Егорова Т.С., Наливайко В.П., Самодурова И.Д. Физика, ч.З: Сборник задач с примерами решений.-М., МТУСИ, 2001.
КОЛЕБАНИЯ И ВОЛНЫ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример I. В начальный момент времени гармонического колебательного движения смещение x(0) материальной точки равно нулю, а скорость v(0) имеет положительное значение. Амплитуда A=8см, период T=2c. Определить уравнение колебаний x(t) материальной точки.
Дано: x(0)=0, v(0)>0, T=2c, A=0,08м.
Найти: x(t).
Решение. Поскольку, по условию, колебательное движение является гармоническим, запишем его уравнение:
![]() (1)
(1)
Из
(I) получаем выражение для скорости ![]() в виде
в виде
![]() (2)
(2)
Используя теперь начальные условия, получим из (1) и (2)
![]() и
и ![]() (3)
(3)
Наименьшее
по величине значение ![]() ,
которым можно удовлетворить условиям,
является
,
которым можно удовлетворить условиям,
является ![]() .
.
Учитывая,
что ![]() ,
получим
,
получим
![]() , (4)
, (4)
или
 .
.
Формула (4) является решением задачи. Действительно, при t = 0 имеем
x
= 0 и, так как
![]() , то
, то ![]() .
.
С
числовыми значениями уравнение колебаний
запишется в виде
![]() ,
м.
,
м.
Пример
2. Материальная
точка совершает гармоническое
колебательное движение с периодом T=4c
и амплитудой A=12см.
Определить скорость ![]() и ускорение
и ускорение ![]() в тот момент времени t,
когда смещение x(t)=4см.
в тот момент времени t,
когда смещение x(t)=4см.
Дано: T=4c, A=0,12м, T=2c, x(t)=0,04м.
Найти: v(t), a(t).
Решение. Запишем уравнение гармонических колебаний материальной точки:
, (1)
где
A
– амплитуда; ![]() – круговая частота;
– круговая частота; ![]() – начальная фаза;
– начальная фаза; ![]() – смещение материальной точки в момент
времени t.
– смещение материальной точки в момент
времени t.
Из
(1) следуют выражения для скорости ![]() и ускорения
и ускорения ![]() материальной точки:
материальной точки:
, (2)
![]() (3)
(3)
Сравнение формул (1) и (3) показывает, что
![]() . (4)
. (4)
Учитывая,
что ![]() ,
получим окончательное выражение для
ускорения из (4):
,
получим окончательное выражение для
ускорения из (4):
![]() . (5)
. (5)
Для нахождения скорости при данном смещении возведем уравнения (1) и (2) в квадрат и запишем их в виде:
![]()
![]() (1)
(1)
![]() (2)
(2)
Складывая (1) и (2), получим
![]()
Отсюда
![]() ,
,
и окончательно
![]() .
(6)
.
(6)
Полученные выражения (5) и (6) дают решение задачи.
Вычисления:
![]() ,
,
![]() .
.
Два
знака в выражении для скорости
соответствуют тому факту, что скорость
материальной точки может иметь два
различных направления при данном ![]() – к положению равновесия и от него.
– к положению равновесия и от него.
Пример
3. Материальная
точка одновременно участвует в двух
гармонических колебаниях, происходящих
вдоль одной прямой. В единицах СИ
уравнения слагаемых колебаний
записываются в виде ![]() и
и ![]() .
Определить
уравнение результирующего колебания
и построить векторную диаграмму
колебаний.
.
Определить
уравнение результирующего колебания
и построить векторную диаграмму
колебаний.
Дано:
![]()
Найти:
![]()
Решение. При сложении двух гармонических колебаний с равными частотами, происходящих вдоль одной прямой, результирующее колебание также будет гармоническим с той же частотой. Следовательно,
![]() (1)
(1)
Таким
образом, решение задачи сводится к
нахождению неизвестных А
и
.
Эти величины выражаются через ![]() следующим образом:
следующим образом:
![]() (2)
(2)
Используя
теорему косинусов в треугольнике ![]() рис.4, получаем
рис.4, получаем
![]() (3)
(3)
Вычисления. Подставляя данные задачи в (2) и (3), получим:
![]()
![]()
Окончательный ответ запишем в виде:
![]()
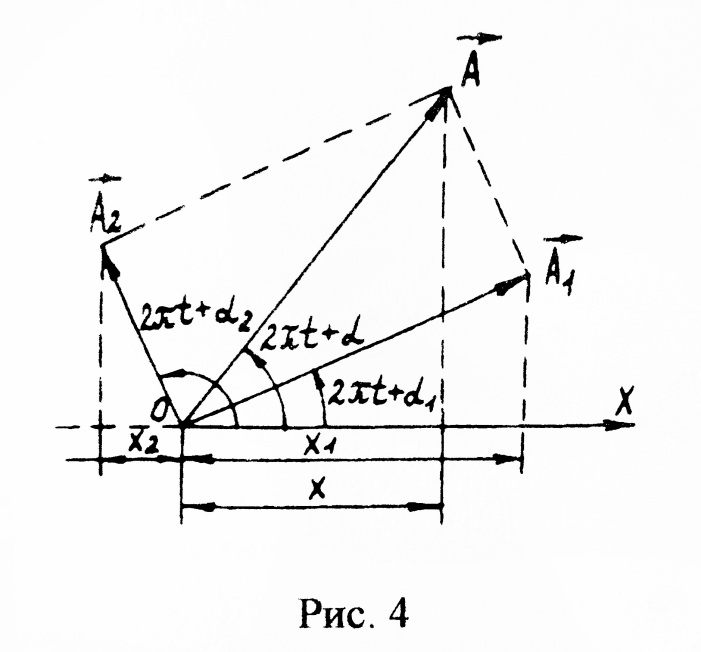
Это
же решение легче получить с помощью
векторной диаграммы (рис.4). С ее помощью
сразу находим величину результирующей
амплитуды
![]() (угол между
(угол между ![]() прямой).
Нарисовав векторную диаграмму для
момента времени t
= 0 (рис.5), получим начальную фазу
в виде
прямой).
Нарисовав векторную диаграмму для
момента времени t
= 0 (рис.5), получим начальную фазу
в виде ![]() .
Нетрудно убедиться в тождественности
обоих решений.
.
Нетрудно убедиться в тождественности
обоих решений.
Пример
4. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
уравнения которых в единицах СИ имеют
вид ![]() и
и ![]() . Определить уравнение траектории
движения
. Определить уравнение траектории
движения
материальной
точки, начертить ее с соблюдением
масштаба и указать ее пределы. Рассчитать
и указать на чертеже скорость ![]() и ускорение
и ускорение ![]() точки в начальный момент времени t
= 0.
точки в начальный момент времени t
= 0.
Дано:
![]()
Найти:
![]()
Решение.
Так как частоты ![]() кратны друг другу, то траекторией
движения материальной точки является
одна из фигур Лиссажу. Для нахождения
уравнения траектории необходимо решить
совместно уравнения движения с целью
исключения времени. В данном случае
это легко сделать, выразив
кратны друг другу, то траекторией
движения материальной точки является
одна из фигур Лиссажу. Для нахождения
уравнения траектории необходимо решить
совместно уравнения движения с целью
исключения времени. В данном случае
это легко сделать, выразив ![]() через
через ![]() с помощью тригонометрической формулы
с помощью тригонометрической формулы
![]() .
Тогда
.
Тогда
![]() (1)
(1)
Из второго уравнения найдем
![]() (2)
(2)
Подставив (2) в (1), получим

или
![]() ;
;
![]() . (3)
. (3)
Полученное уравнение является уравнением параболы.
Чтобы правильно начертить эту траекторию, учтем, что движение материальной точки происходит в пределах
![]()
что видно из исходных уравнений. Нам нужно определить скорость и ускорение материальной точки в момент времени t = 0.
Д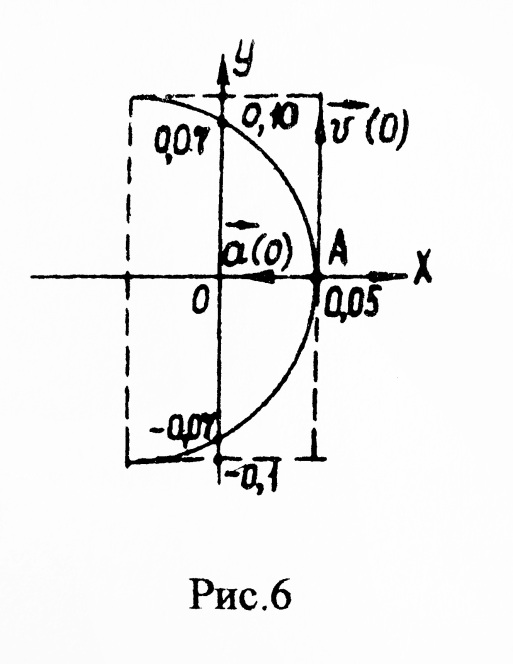 ля
этого определим сначала координаты
материальной точки при t
= 0. Из исходных уравнений имеем
ля
этого определим сначала координаты
материальной точки при t
= 0. Из исходных уравнений имеем ![]() т.е. материальная точка находится при
t
= 0 в вершине (точка А) параболы (рис.6).
Для нахождения скорости и ускорения
материальной точки найдем сначала
составляющие скорости и ускорения по
осям Х и У:
т.е. материальная точка находится при
t
= 0 в вершине (точка А) параболы (рис.6).
Для нахождения скорости и ускорения
материальной точки найдем сначала
составляющие скорости и ускорения по
осям Х и У:
![]()
![]() ; (4)
; (4)
![]()
и
![]() . (5)
. (5)
При t = 0 имеем из (4) и (5):
![]()
Векторы
![]() показаны
на рис.6. Численные их значения равны
показаны
на рис.6. Численные их значения равны
![]()
![]()
Пример
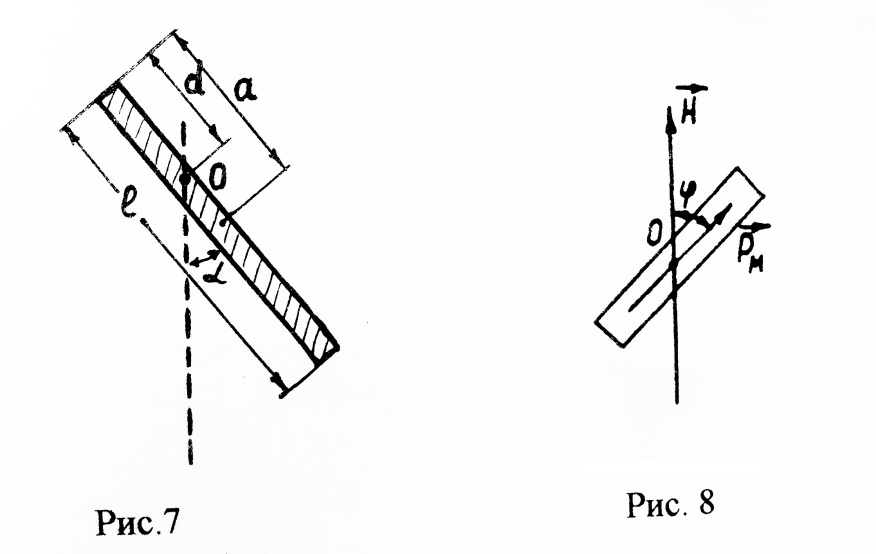
5. Однородный
шест (стержень) длиной ![]() совершает свободные колебания в
вертикальной плоскости вокруг
горизонтальной оси, проходящей через
точку О и отстоящей на
совершает свободные колебания в
вертикальной плоскости вокруг
горизонтальной оси, проходящей через
точку О и отстоящей на ![]() от его верхнего конца. Составить
дифференциальное уравнение колебаний
стержня, записать его решение, найти
циклическую частоту и период колебаний.
Трением пренебречь.
от его верхнего конца. Составить
дифференциальное уравнение колебаний
стержня, записать его решение, найти
циклическую частоту и период колебаний.
Трением пренебречь.
Дано:
![]()
Найти:
![]()
Решение. В процессе колебаний стержень, который можно рассматривать как физический маятник (см. рис.7 и 8), совершает вращательное движение под действием момента силы тяжести
![]() . (1)
. (1)
Здесь
![]() расстояние между точкой подвеса и
центром инерции тела,
расстояние между точкой подвеса и
центром инерции тела, ![]() угол поворота. Момент реакции опоры
относительно горизонтальной оси
закрепления OZ – равен нулю. Основное
уравнение динамики вращательного
движения маятника
угол поворота. Момент реакции опоры
относительно горизонтальной оси
закрепления OZ – равен нулю. Основное
уравнение динамики вращательного
движения маятника
![]() (2)
(2)
где
![]() угловое
ускорение,
угловое
ускорение, ![]() момент инерции. Его значение, поскольку
ось вращения не проходит через центр
инерции, определяется теоремой Штейнера
момент инерции. Его значение, поскольку
ось вращения не проходит через центр
инерции, определяется теоремой Штейнера
![]() (3)
(3)
Подставляя выражения (1) и (3) в уравнение (2), приходим к равенству
![]()
С
учетом, что ![]() для малых углов колебаний, окончательно
имеем
для малых углов колебаний, окончательно
имеем
![]() (4)
(4)
где
![]() собственная циклическая частота
гармонических колебаний маятника,
описываемых дифференциальным уравнением
(4). Его решение для углового смещения
собственная циклическая частота
гармонических колебаний маятника,
описываемых дифференциальным уравнением
(4). Его решение для углового смещения
![]()
Значения
амплитуды колебаний ![]() и начальной фазы
и начальной фазы ![]() определяются заданием начальных условий
колебаний t
= 0.
определяются заданием начальных условий
колебаний t
= 0.
Итак:
![]()
![]()
Вычисление:
![]()
![]()
Пример
6. В однородном
магнитном поле напряженностью ![]() намагниченный стержень совершает
гармонические колебания (рис.8). Ось
вращения стержня проходит через его
середину в точке О, Период колебаний
стержня
намагниченный стержень совершает
гармонические колебания (рис.8). Ось
вращения стержня проходит через его
середину в точке О, Период колебаний
стержня ![]() .
Длина стержня
.
Длина стержня ![]() ,
масса
,
масса ![]() .
Определить
магнитный момент стержня.
.
Определить
магнитный момент стержня.
Дано:
![]()
Найти:
![]()
Решение. Составим дифференциальное уравнение колебаний стержня. Будем описывать отклонение стержня от положения равновесия (направление
магнитного
поля) углом ![]() .
Основное уравнение вращательного
движения запишем в виде
.
Основное уравнение вращательного
движения запишем в виде
![]() (1)
(1)
где
![]() момент сил, действующих на стержень со
стороны магнитного поля;
момент сил, действующих на стержень со
стороны магнитного поля;
B – индукция магнитного поля;
J – момент инерции стержня относительно оси колебаний, проходящей через точку О перпендикулярно стержню.
Легко
видеть из (1), что гармоническое колебание
будет происходить лишь в случае малых
углов отклонения (![]() ).
).
Тогда уравнение (1) приобретает вид
![]()
что совпадает с дифференциальным уравнением гармонических колебаний, где квадрат круговой частоты
![]() . (2)
. (2)
Учитывая,
что ![]() получим из (2) искомое выражение для
магнитного момента
получим из (2) искомое выражение для
магнитного момента
![]() (3)
(3)
Проверим наименование результата по расчетной формуле:

Вычисление:
![]()
Пример
7. Электрический
контур (рис.9) состоит из последовательно
соединенных катушки индуктивности ![]() Гн
и двух конденсаторов
Гн
и двух конденсаторов
![]() мкФ
и
мкФ
и ![]() мкФ,
разделенных активным сопротивлением
мкФ,
разделенных активным сопротивлением
![]() КОм.
Составить, исходя из 2-го закона Кирхгофа,
дифференциальное уравнение колебании
заряда в системе и записать его решение.
Найти циклическую частоту, период и
время релаксации колебаний
КОм.
Составить, исходя из 2-го закона Кирхгофа,
дифференциальное уравнение колебании
заряда в системе и записать его решение.
Найти циклическую частоту, период и
время релаксации колебаний ![]() .
.
Дано:
![]() .
.
Найти:
дифференциальное уравнение, его решение
![]()
Р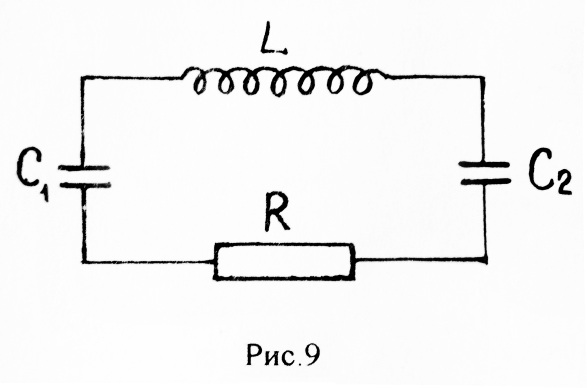 ешение.
Считая,
что в контуре действует лишь одна э.д.c.
самоиндукции
ешение.
Считая,
что в контуре действует лишь одна э.д.c.
самоиндукции ![]() второй закон Кирхгофа
второй закон Кирхгофа
для электрического контура рис.9 запишем в виде
![]() (1)
(1)
здесь
i
– сила тока
в цепи, ![]() напряжение на элементах контура.
напряжение на элементах контура.
Так
как ![]() соотношение (1) эквивалентно уравнению
соотношение (1) эквивалентно уравнению
![]()
или
![]() (2)
(2)
где
![]() коэффициент затухания,
коэффициент затухания, ![]() квадрат собственной частоты колебаний
квадрат собственной частоты колебаний
![]()
Решением дифференциального уравнения затухающих колебаний (2) является уравнение затухающих колебаний
![]() (3)
(3)
Здесь
![]() начальная амплитуда,
начальная амплитуда, ![]() соответственно циклическая частота и
начальная фаза колебаний. При этом
соответственно циклическая частота и
начальная фаза колебаний. При этом
![]()
Вычисления:

![]()
Пример
8. В
колебательном контуре, имеющем
сопротивление
![]() происходят затухающие колебания.
Определить индуктивность контура
происходят затухающие колебания.
Определить индуктивность контура ![]() ,
если за промежуток времени
,
если за промежуток времени ![]() амплитудное значение заряда на обкладках
конденсатора уменьшится в 3 раза.
амплитудное значение заряда на обкладках
конденсатора уменьшится в 3 раза.
Дано:
![]() Ом,
t
= 0,01с,
Ом,
t
= 0,01с,
![]() 3.
3.
Найти:
![]()
Решение. В данной задаче имеем затухающие колебания заряда (на обкладках конденсатора) в колебательном контуре. Амплитудное значение величины этого заряда уменьшается во времени по закону
![]() (1)
(1)
где коэффициент затухания в электрическом контуре. Тогда из (1) имеем
![]()
откуда путем логарифмирования получаем выражение для искомой индуктивности
![]()
Вычисление:
![]()
Пример
9. Математический
маятник длиной ![]() совершает гармонические колебания.
Когда этот маятник поместили в вязкую
жидкость, то оказалось, что логарифмический
декремент затухания
совершает гармонические колебания.
Когда этот маятник поместили в вязкую
жидкость, то оказалось, что логарифмический
декремент затухания ![]() равен 3,6. Определить, на сколько изменился
период колебаний маятника.
равен 3,6. Определить, на сколько изменился
период колебаний маятника.
Дано:
![]()
Найти:
![]()
Решение. Определить период колебаний маятника до помещения его в вязкую среду
![]() (1)
(1)
После помещения в вязкую среду колебания маятника будут затухающими, поэтому его период выразится формулой
![]() (2)
(2)
(здесь
использованы известные соотношения
![]() и
и
![]() ).
).
Возведя
обе части равенства (2) в квадрат и решая
его относительно ![]() ,
получим:
,
получим:
![]()
Искомое
изменение периода ![]() находим как разность
находим как разность
![]()
Вычисление:
![]()
Пример
10. Определить
относительную убыль энергии колебаний
в последовательном ![]() контуре за период, если известно, что
за
контуре за период, если известно, что
за ![]() полных колебаний она уменьшается в
полных колебаний она уменьшается в ![]() раз. Чему равна добротность колебаний
раз. Чему равна добротность колебаний
![]() ?
?
Дано:
![]()
Найти:
![]()
Решение. Энергия электрического поля конденсатора пропорциональна квадрату амплитуды (заряда или напряжения)
![]()
Нами учтено, что амплитуда колебаний заряда уменьшается по экспоненциальному закону
![]()
Таким образом, для амплитуды колебаний энергии можно записать
![]()
Соответственно, для логарифмического декремента затухания имеем
![]() (1)
(1)
Добротность контура , логарифмический декремент затухания связаны соотношением
![]() (3)
(3)
где
![]() относительная убыль энергии. Получим
окончательно
относительная убыль энергии. Получим
окончательно
![]() (4)
(4)
Вычисление выполним в соответствии с формулами (1) и (4):
![]()
![]() .
.
Пример
11. В
электрическом колебательном контуре,
содержащем последовательно соединенные
катушку индуктивности
,
активное сопротивление ![]() амплитуда напряжения уменьшается в
амплитуда напряжения уменьшается в
![]() раз за
раз за ![]() полных колебаний. Значение критического
сопротивления, при котором колебания
прекращаются и процесс становится
апериодическим,
полных колебаний. Значение критического
сопротивления, при котором колебания
прекращаются и процесс становится
апериодическим, ![]() Найти индуктивность катушки и активное
сопротивление контура.
Найти индуктивность катушки и активное
сопротивление контура.
Дано:
![]()
Найти:
![]()
Решение. Закон колебаний электрического заряда на обкладках конденсатора
![]()
где
![]()
![]() ,
, ![]()
В
случае критического режима ![]() частота колебаний
частота колебаний ![]() и при этом
и при этом
![]()
![]()
Откуда:
![]()
Величину
![]() можно найти, используя связь
логарифмического декремента затухания
и коэффициента затухания
можно найти, используя связь
логарифмического декремента затухания
и коэффициента затухания ![]() :
:
![]()
Откуда
с учетом малого затухания ![]() следует
следует
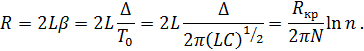
Вычисления:
![]()
![]()
Пример 12. Значения реактивных индуктивного и емкостного сопротивлений последовательного R - L - C контура, в котором совершаются вынужденные колебания с амплитудой напряжения на конденсаторе Uc,m=65,4В, при частоте колебаний 104с-1, равны: RL = 200 Ом и RС = 250 Ом, активное сопротивление контура R = 120 Ом.
Найти амплитуду вынуждающей э.д.с. и максимальное значение (амплитуду) заряда на обкладках конденсатора.
Дано: RL = 200Ом, Rc = 250Om, R = 120 Ом, Uc,m = 65,4В, ω = 104с-1.
Найти: Ет , qc,m .
Р е ш е н и е . Реактивные сопротивления элементов цепи даются выражениями
![]()
что сразу позволяет определить емкость конденсатора
![]()
Амплитуда вынужденных колебаний напряжения на обкладках конденсатора определяется по формуле
Это с учетом выражений (1) и (2) позволяет записать
 /
/
![]() .
.
Амплитудное значение заряда на обкладках конденсатора равно
![]()
Вычисления:
![]()
![]()
![]()
й ![]()
Пример 13. Резонансные колебания в некоторой системе с массой т=0,1кг в единицах СИ описываются уравнением х = 0,08соs(2πt + π/6). Система совершает колебания в среде, коэффициент сопротивления которой r = 0,5 кг/с.
Найти уравнение колебаний F(t) вынуждающей силы (с числовыми коэффициентами), если ее начальная фаза αF = π/2.
Дано: т = 0,1кг , х = 0,08соs(2πt + π/6), r = 0,5 кг/с.
Найти: F(t).
Р е ш е н и е . В системе происходят вынужденные колебания, при которых вынуждающая сила имеет вид
F(t) = F0 cos(ωpt + αF) . (1)
Из (1) видно, что решение данной задачи сводится к определению амплитуды вынуждающей силы F0 . Так как амплитуда А и отставание фазы вынужденных колебаний от фазы вынуждающей силы αF - αх имеют вид

то при резонансе (который имеет место в данной задаче)
![]()
и эти выражения становятся равными

Совместное решение уравнений (3) позволяет определить величину F0. Из
второго
уравнения (3) определяем ![]() и подставляем в первое уравнение,
получая
и подставляем в первое уравнение,
получая
![]()
Таким образом, имеем окончательное выражение для F(t):
![]()
Вычисление:
![]()
![]()
Пример 14. Уравнение колебаний напряжения на пластинах конденсатора в колебательном контуре в единицах СИ имеет вид
![]() Емкость
Емкость
конденсатора С= 0,1 мкФ. Определить уравнение колебаний энергии конденсатора WС(t) .
Дано: U(t), C=0,1 мкФ.
Найти: WС(t), WL(t) .
Р е ш е н и е . Энергия конденсатора в колебательном контуре определяется выражением
![]()
Поскольку колебания гармонические, то полная энергия контура, равная сумме энергий конденсатора и катушки, постоянна:
![]()
Так
как ![]() ,
то из (2) имеем
,
то из (2) имеем
![]()
Выражая
![]() и
и
![]() через
через
![]() ,
получим из (1) и (3) решение задачи, из
которого видно, что колебания энергий
конденсатора и катушки происходят с
частотой в 2 раза большей, чем частота
колебаний напряжения на обкладках
конденсатора:
,
получим из (1) и (3) решение задачи, из
которого видно, что колебания энергий
конденсатора и катушки происходят с
частотой в 2 раза большей, чем частота
колебаний напряжения на обкладках
конденсатора:
![]()
Вычисления:
![]()
![]()
![]()
Пример 15. Плоская упругая волна распространяется со скоростью v=300м/с. Длина волны λ = 3м, амплитуда А = 1мкм. Написать уравнение волны s(x,t) (с числовыми коэффициентами), произвольно выбрав начальные условия.
Дано: v = 300м/с, λ = 3м, А = 1мкм.
Найти; s(x,t).
Р е ш е н и е . Уравнение плоской волны имеет вид
![]()
Где s(x,t) – смещение точки с координатой х в момент времени t;
ω – циклическая частота; k – волновое число; α – начальная фаза.
В
уравнении (1) неизвестная фаза волны
![]() .
Поскольку
начальные условия произвольны, то
выберем α
= 0,
а оставшееся выражение преобразуем к
.
Поскольку
начальные условия произвольны, то
выберем α
= 0,
а оставшееся выражение преобразуем к
виду:
![]()
так
как ![]() .
.
Подставляя (2) и (1), получим искомое уравнение волны
![]()
которое с числовым коэффициентом имеет вид
![]()
Пример 16. Плоская электромагнитная волна распространяется в среде с диэлектрической проницаемостью ε = 4 и магнитной проницаемостью μ = 1. Интенсивность волны I = 26Вт/м2. Период колебаний Т = 2мкс. Определить уравнение электромагнитной волны, произвольно выбрав начальные условия. При решении задачи следует учесть, что среднее значение квадрата синуса (либо косинуса) за период равно 0,5.
Дано: ε = 4, μ = 1, I = 26Вт/м2, T = 2 мкс.
Найти: E(x,t), H(x,t).
Р е ш е н и е . Уравнение плоской электромагнитной волны имеет вид
![]()
![]()
где E0 и H0 - соответственно амплитуды напряженностей электрического и
магнитного полей; 𝜔 - циклическая частота волны; k - волновое число; α -
начальная фаза.
Прежде всего, для простоты положим, согласно условию, α = 0. Тогда фазу
волны можно записать в форме
![]()
Теперь
учтем, что ![]() (с- скорость света в вакууме). Поэтому
(с- скорость света в вакууме). Поэтому

Амплитуды Е0 и H0 можно связать с интенсивностью волны. Так как интенсивность волны есть среднее во времени значение величины вектора Пойнтинга, то
![]()
В электромагнитной волне Е0 и H0 связаны соотношением
![]()
Используя формулы (3) и (4), получим

Учитывая
также, что ![]() , из (5) имеем
, из (5) имеем
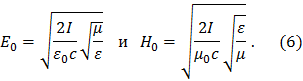
Проверим наименования результатов по расчетным формулам:

Подставляя (2) и (6) в (1), запишем искомое уравнение электромагнитной волны:

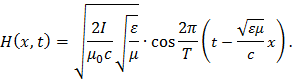
Вычисления:


![]()
![]()
![]()
![]()
Пример 17. Плоская звуковая волна, уравнение которой в единицах СИ
![]() ,
распространяется в воздухе, плотность
которого ρ=0,0013
г/см3.
Найти
интенсивность волны I
и уравнение колебаний плотности потока
энергии J(x,t)
c
числовыми
коэффициентами, вычислив ее значение
J(x0,t0)
для
момента
времени t0=1мc
и
координаты х0=1.
При
решении задачи следует учесть, что
среднее значение квадрата синуса за
период
равно
0,5.
,
распространяется в воздухе, плотность
которого ρ=0,0013
г/см3.
Найти
интенсивность волны I
и уравнение колебаний плотности потока
энергии J(x,t)
c
числовыми
коэффициентами, вычислив ее значение
J(x0,t0)
для
момента
времени t0=1мc
и
координаты х0=1.
При
решении задачи следует учесть, что
среднее значение квадрата синуса за
период
равно
0,5.
Р е ш е н и е . Запишем уравнение плоской звуковой волны, заданной в условии, в виде
![]()
Плотность потока энергии U(x,t) можно вычислить по формуле
![]()
где v - скорость распространения волны; w(x,t) - объемная плотность энергии в точке х в момент времени t, которая для упругой волны определяется выражением
![]()
Данное выражение (3) для плотности энергии w(x,t) получается в результате суммирования плотности кинетической энергии wk и плотности потенциальной энергии wp с учетом того, что фазы колебаний этих wk и wP совпадают и эти плотности равны по величине. Для написания этой формулы нужно учесть, что dm есть масса частиц упругой среды (воздуха), заключенная в объеме dV, а u есть скорость колебаний этих частиц, т.е.
u=dy/dt.
Вычислив производную из уравнения (1)
![]()
и подставляя ее в (3), получим
![]()
Скорость волны и определим как отношение ω и k:
![]()
Подставив (4) и (5) в (2), получим:
![]()
Интенсивность волны - это среднее во времени значение величины плотности потока энергии. Усредняя выражение (6) по времени, получаем интенсивность волны
![]()
Проверим наименование результата по расчетной формуле:

Вычисления:
![]()
![]()
![]()
![]()
Пример 18. В опыте Юнга щели освещаются монохроматическим светом (λ= 0,6 мкм). Расстояние между щелями d = 1мм, расстояние от щели до экрана L = Зм. Определить расстояние между максимумами яркости смежных интерференционных полос на экране.
Дано: λ = 0,6 мкм = 0,6·10-6 м, d = 1мм=10-3 м, L = 3м.
Найти: Δу.
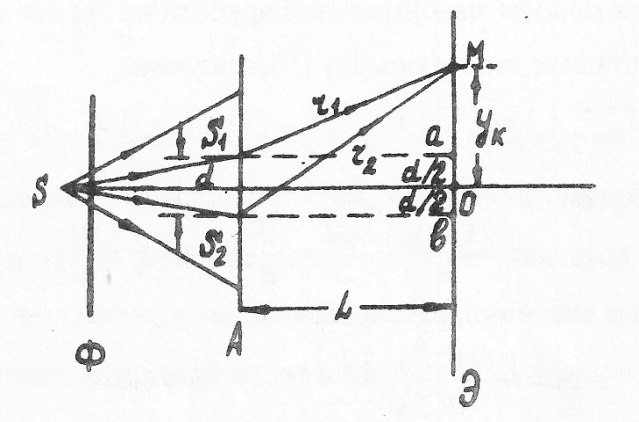
Рис. 10
Р е ш е н и е . В опыте Юнга (см. рис. 10) источниками когерентных волн являются две узкие щели S1 и S2 в непрозрачной пластине А, перпендикулярные чертежу. Первичным источником света служит ярко освещенная щель S, параллельная S1 и S2, и находящаяся от них на одинаковом расстоянии. Светофильтр Ф пропускает свет заданной длины волны (от λ до λ±Δλ). Интерференционная картинка, получаемая на экране Э, представляет собой полосы, параллельные щелям S, S1, S2.
Искомое расстояние между максимумами яркости смежных интерференционных полос на экране Э–Δу определяется как разность расстояний от центра картины
(точка О) до двух соседних полос номера k и k +1:
![]()
Найдем эти расстояния. Допустим, что максимум k-го порядка проходит через точку М, а расстояние ук = ОM. Из прямоугольных треугольников S1Ma и S2Mb имеем
![]()
![]()
Вычитая
из (2) выражения (3), получим:
![]()
Или
![]()
В
выражении (4) ![]() - разность хода между лучами r1
и
r2
,
- разность хода между лучами r1
и
r2
,
а
r1
+
r2=2L.
Так
как L>>d,
следовательно,
![]() и
при этом
и
при этом
![]()
Условием получения полосы максимальной яркости на экране является
![]() и,
подставляя это в формулу (5), получим:
и,
подставляя это в формулу (5), получим:
![]()
По формуле (1) находим:
![]()
Подставляя числовые значения, рассчитываем Δу:
![]()
Пример 19. Пучок параллельных лучей (λ = 0,6мкм) падает под углом i = 30° на мыльную пленку (n2=4/3≈1,33). При какой наименьшей толщине
пленки отраженные лучи будут максимально ослаблены интерференцией?
Максимально усилены?
Дано: λ = 0,6мкм = 0,6·10-6 м , i = 30°, n2=4/3≈1,33.
Найти: dmin .
Р е ш е н и е . Из пучка параллельных лучей, падающих на пленку, выделим один луч SA (рис.11). В точках А и В падающий луч частично отражается и
частично преломляется. Лучи 1 и 2 собираются линзой (на чертеже не указано) и в ее фокусе интерферируют. Полная разность хода между лучами 1 и 2 будет
![]()
так как
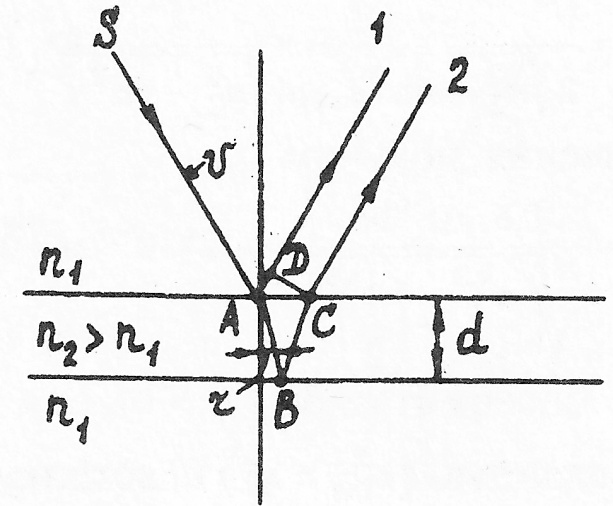
Рис. 11
![]()
Второе слагаемое λ/2 обусловлено тем, что у луча 1 при отражении от более плотной среды в точке А фаза вектора Е скачком меняется на π рад, что соответствует изменению разности хода лучей на λ/2.
А) Максимально ослаблены отраженные лучи будут при условии:
![]()
откуда

а

Подставляя числовые значения, получим
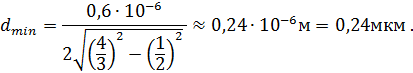
Б) Максимально усилены отраженные лучи будут при условии
![]()
откуда

а
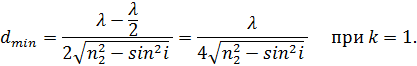
Подставляя числовые значения, получим

Пример 20. На стеклянную (ncm=1,5) пластинку нанесена мыльная пленка n2=4/3≈1,33, толщина d = 3,5·10-7м. Параллельный пучок лучей белого света падает на пленку под углом 60°. Какого цвета пленка в отраженном свете?
Дано: ncm=1,5, n2=4/3≈1,33, i = 60° d = 3,5·10-7м.
Найти: λi .
Р е ш е н и е . Содержание этой задачи отличается от предыдущей тем, что мыльная пленка нанесена на стеклянную поверхность, показатель преломления которой ncm > n2 (рис. 12).

Вследствие этого оба луча 1 и 2 отражаются от более плотной среды в точках А и В соответственно, при этом у обоих лучей векторы Е меняют фазу на л рад, что не вносит никаких изменений в оптическую разность хода, поэтому
![]()
Рис. 12
Так как толщина d одинакова во всех точках пленки и лучи падают параллельно, т.е. под одним углом, а показатель преломления одинаков для всех точек пленки, то разность хода Δ лучей будет иметь одно и то же значение для всех точек пленки и на ней не будет никаких полос, она будет либо окрашена в какой-то цвет и либо темная.
Условия усиления света:
![]()
откуда получаем

При k=0 λ0→∞,
k=1 λ1≈7,1·10-7м – область красного цвета
k=2 λ2≈3,55·10-7м – область ультрафиолетовых лучей.
Следовательно, λi ≈ 7,1·10-7м, т.е. в отраженном свете она будет красного цвета. Размерность результата: [λ] = м, так как [d] = м, а все остальные величины безразмерны.
Пример 21. На стеклянный клин нормально к его грани падает параллельный пучок монохроматического света с длиной волны λ = 0,6мкм. Число т интерференционных полос, приходящихся на l = 1см, равно 10. Определить угол α клина.
Дано: λ = 0,6мкм = 0,6·10-6м, l = 1см - 0,01м, т =10.
Найти: α .
Р е ш е н и е . Лучи, падая нормально у грани клина, отражаются как от верхней, так и от нижней грани. Эти лучи когерентны. Поэтому вблизи поверхности клина будут наблюдаться интерференционные полосы. Так как угол клина мал, то отраженные лучи 1 и 2 (рис. 13) будут практически параллельны. Темные полосы видны на тех участках, для которых разность хода лучей кратна нечетному числу половины длин волн
![]()
где k=0,1,2,.....
Разность
хода Δ двух лучей складывается из
разности оптических путей этих лучей
2dncosi2
и половины длины волны λ
/2.
Величина λ
/2 представляет
собой добавочную разность хода,
возникающую при отражении луча от
оптически более плотной среды за счет
изменения фазы ![]() на
π рад.
на
π рад.

Рис. 13
Подставляя в формулу (1) значение разности хода Δ лучей, получим
![]()
где n - показатель преломления стекла (n =1,5); dk - толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k;
r – угол преломления.
Согласно условию, угол падения равен нулю, следовательно и угол преломления r равен нулю, a cosr =1. Раскрыв скобки в правой части
равенства (2), после упрощения получим
![]()
Пусть произвольной темной полосе номера k соответствует толщина dk клина, а темной полосе номера k+m - толщина dk+m клина. Тогда из рис.15, учитывая, что т полос укладывается на расстоянии l, найдем
![]()
Найдем из (3) dk и dk+m и подставим их в формулу (4). Затем, учитывая, что из-за малости угла sinα=α, получим
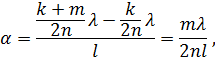
![]()
Подставляя числовые значения физических величин, найдем:
![]()
Выразим α в секундах, воспользовавшись соотношением между радианом и
секундой:
![]()
![]()
Пример 22. Между стеклянной пластинкой (n2 = 1,70) и лежащей на ней плосковыпуклой линзой (n1 = 1,52) находится жидкость (nж =1,41). Найти радиус r10 десятого темного кольца Ньютона при наблюдении его в отраженном свете (λ = 0,7мкм), если радиус кривизны линзы R = 1,0м, а свет падает перпендикулярно плоской поверхности линзы.
Дано: n1 = 1,52, n2 = 1,70, nж =1,41, R = 1,0м, λ = 0,7мкм=0,7·10-6м, k=10.
Найти: r10 .
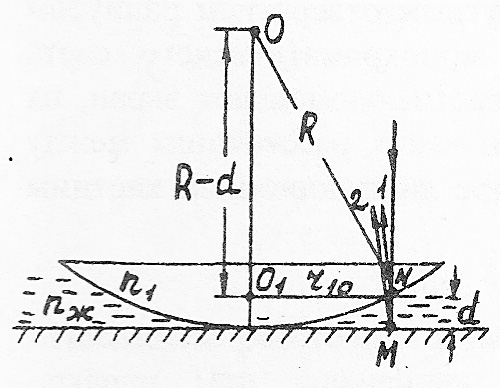
Р е ш е н и е . Монохроматический луч света, перпендикулярный плоской поверхности линзы, частично отражается и частично преломляется в точках N и М (рис.14). Оптическая разность хода лучей 1 и 2 Δопт=2dnжcosr=2dnж, так как лучи падают нормально, и углы падения i и преломления r равны
Рис. 14
нулю
(угол преломления r
несколько отличен от нуля, но при большом
радиусе кривизны R он близок к нулю).
Полная разность хода лучей 1 и 2 отличается
от оптической на λ/ 2, так как луч 1 в
точке N отражается от менее плотной
среды (nж
< n1),
при этом фаза ![]() не меняется, а луч 2 в точке М отражается
от более плотной среды (n2
> nж),
при этом фаза
скачком изменяется на π рад, что
соответствует разности сти хода на
λ/2. Следовательно, имеем:
не меняется, а луч 2 в точке М отражается
от более плотной среды (n2
> nж),
при этом фаза
скачком изменяется на π рад, что
соответствует разности сти хода на
λ/2. Следовательно, имеем:
![]()
Из треугольника O1ON по теореме Пифагора найдем r10:
![]()
![]()
пренебрегая знамением d2<<2Rd, получаем:
![]()
Толщину зазора d в точках расположения десятого темного кольца найдем, решая совместно (2) и (1) и учитывая, что для темного кольца полная разность хода равна нечетному числу λ/2:
![]()
или ![]()
откуда ![]() .
.
Подставляя (3) в формулу (2), имеем:

с учетом числовых значений, получим:

Пример 23. На непрозрачную пластину с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок монохроматического света (λ = 750нм). На пути лучей, прошедших через отверстие, помещают экран, на котором наблюдается дифракционная картина. При каких расстояниях между пластиной и экраном, превышающих 20 см, в центре дифракционной картины будет наблюдаться темное пятно?
Дано: r =1мм = 10-3 м, λ = 750 нм = 0,75·10-6м , R=20см.
Найти: R .
Р е ш е н и е . Расстояние R, при котором в центре дифракционной картины будет наблюдаться темное пятно, определяется числом зон Френеля, укладывающихся в отверстии:
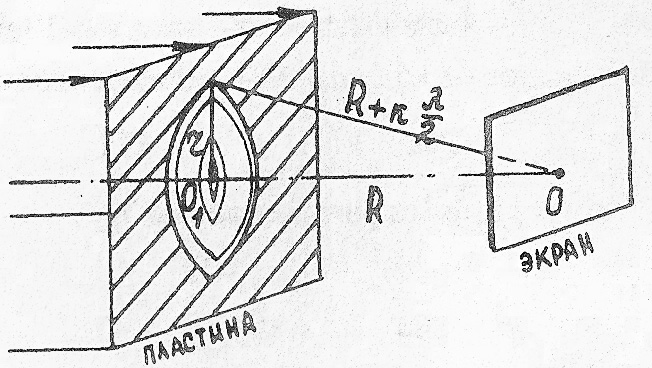
Рис. 15
если число зон k - четное, то в центре картины наблюдается темное пятно. Если в отверстии укладывается k зон Френеля (рис.15), то расстояние от центра экрана 0 до края отверстия на кλ/2 больше, чем расстояние между центрами экрана и отверстия О1О = R. По теореме Пифагора имеем
![]()
или
![]()
Слагаемое
![]() и
им можно пренебречь, поэтому
и
им можно пренебречь, поэтому
![]()
Как указывалось выше, значение k должно быть четным, т.е. k = 2,4,6,8... Найдем значения R > 20см, при которых в центре экрана будет темное пятно:
![]()
![]()
![]()
![]()
Последнее расстояние (при k = 8) меньше 20 см и не удовлетворяет условию задачи. При дальнейшем увеличении k расстояние R будет еще меньше.
Следовательно, искомыми расстояниями будут 66,7см; 33,3см; 22,2см. Выполним проверку наименования результатов по формуле (1):
Пример 24. На пластину П со щелью шириной а=0,1мм нормально падает монохроматический пучок света (λ=0,6мкм). Определить ширину центрального максимума в дифракционной картине на экране Э, расположенном в фокальной плоскости линзы L с фокусным расстоянием F=1м.
Дано: а=0,1мм= 10-4м, λ =0,6мкм = 0,6·10-6м , F = 1м .
Найти: АВ.
Р е ш е н и е . Ширину центрального максимума (рис. 16) примем примерно равной расстоянию АВ между верхним и нижним ближайшими минимумами
д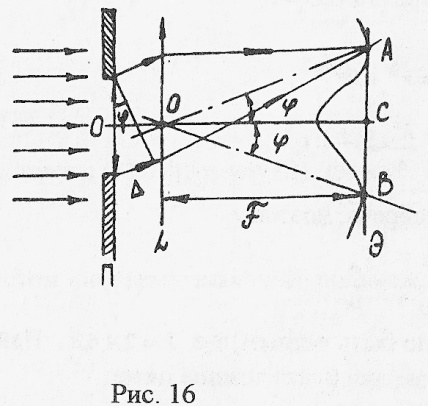 ифракционной
картины, получаемой с помощью линзы L
на экране Э. Минимумы интенсивности
получаются под углами φ,
при которых разность хода лучей Δ равна
четному числу полуволн (для первого
минимума двум полуволнам). При этом
щель а
в пластине П разбивается на четное
число зон Френеля, а колебания, пришедшие
в точки А и В от любых двух соседних
зон, гасят друг друга, так как противоположны
по фазе.
ифракционной
картины, получаемой с помощью линзы L
на экране Э. Минимумы интенсивности
получаются под углами φ,
при которых разность хода лучей Δ равна
четному числу полуволн (для первого
минимума двум полуволнам). При этом
щель а
в пластине П разбивается на четное
число зон Френеля, а колебания, пришедшие
в точки А и В от любых двух соседних
зон, гасят друг друга, так как противоположны
по фазе.
Разность хода между лучами, огибающими края щели,
![]() где
к = 1,2,3,4... (в нашем случае для первых
минимумов k
= 1). Искомое расстояние АВ находим из
чертежа (рис. 16):
где
к = 1,2,3,4... (в нашем случае для первых
минимумов k
= 1). Искомое расстояние АВ находим из
чертежа (рис. 16): ![]() ,
так как для
малых
углов tg φ
= sinφ
≈ φ
в радианах. Найдем значение sinφ
из
(1) и получим
окончательное
выражение для АВ:
,
так как для
малых
углов tg φ
= sinφ
≈ φ
в радианах. Найдем значение sinφ
из
(1) и получим
окончательное
выражение для АВ: ![]() , так как к = 1,
, так как к = 1,
![]() Выполним
проверку наименований результата по
расчетной формуле:
Выполним
проверку наименований результата по
расчетной формуле:
![]() Пример
25.
На грань кристалла каменной соли падает
параллельный пучок рентгеновских лучей
λ = 1,5∙10-10м.
Определить
расстояние между атомными плоскостями
кристалла, если дифракционный максимум
второго порядка определяется, когда
лучи падают под углом φ
=
32°30' к поверхности кристалла.
Пример
25.
На грань кристалла каменной соли падает
параллельный пучок рентгеновских лучей
λ = 1,5∙10-10м.
Определить
расстояние между атомными плоскостями
кристалла, если дифракционный максимум
второго порядка определяется, когда
лучи падают под углом φ
=
32°30' к поверхности кристалла.
Дано: λ = 1,5∙10-10м, k = 2, φ = 32°30'.
Найти: d .
Р е ш е н и е . При дифракции рентгеновских лучей на кристаллической решетке направления, в которых определяются дифракционные максимумы, находятся из уравнения Вульфа-Брегга:
![]()
где
d
- расстояние между атомными плоскостями
кристалла; φ - угол между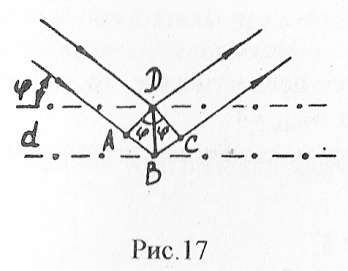
направлением пучка параллельных рентгеновских лучей, падающих на кристалл, и гранью кристалла (рис.17).
Из формулы (1) находим
![]()
Пример 26. На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2мкм. Какого наибольшего порядка дифракционный максимум дает эта решетка в случае красного света (λ1 = 0,7мкм) и в случае фиолетового (λ2 =0,41мкм)? Под какими углами к главной оптической оси линзы они расположены?
Дано: d=а + b = 2мкм = 2∙10-6 м, λ1 = 0,7мкм=0,7∙10-6 м,
λ2 =0,41мкм=0,41∙10-6 м.
Найти: mmax , φmax .
Р
е ш е н и е . На основании известной
формулы дифракционной решетки (Р) ![]() ,
напишем следующее выражение для значения
порядка дифракционного максимума
(рис.18)
,
напишем следующее выражение для значения
порядка дифракционного максимума
(рис.18)
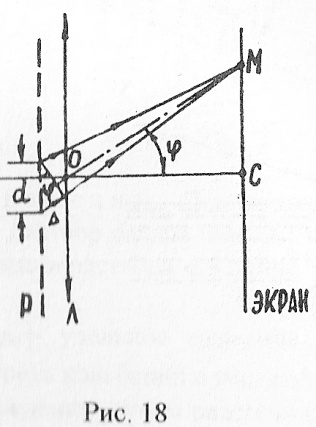
![]()
где d - период решетки; φ - угол между направлением на дифракционный максимум и нормалью к решетке (главной оптической оси линзы Л); λ - длина волны монохроматического света.
Так как sinφ не может быть больше 1, то как это следует из формулы (1), число т не может быть больше d/λ, т.е.
![]()
Подставив в формулу (2) числовые значения, получим: для красных лучей
![]()
для фиолетовых лучей
![]()
Если учесть, что порядок максимумов является целым числом, то найдем, что для красного цвета ттах = 2 и для фиолетового mтах = 4.
Максимум второго порядка красного света наблюдается под углом, синус которого равен
![]()
![]()
Максимум четвертого порядка синего света наблюдается под углом, синус которого равен
![]()
![]()
Пример 27. Естественный луч света падает на полированную поверхность стеклянной пластины (nсm=1,5), погруженной в жидкость. Отраженный от пластины луч образует угол φ= 97° с падающим лучом (рис.19). Определить показатель преломления п1 жидкости, если отраженный свет полностью поляризован. Какой наименьший угол γ составляет преломленный луч с падающим?
Дано: 2i1= φ = 97°, п2 = пст = 1,5.
Найти: п1 и γ .
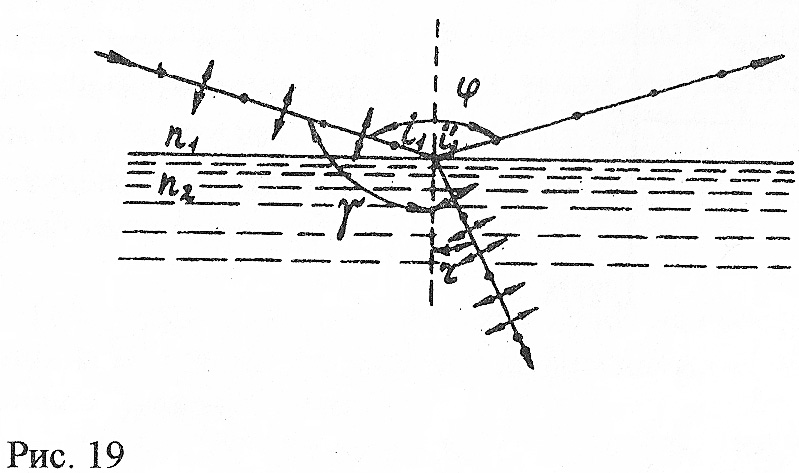
Р е ш е н и е . Согласно закону Брюстера, луч света, отраженный от диэлектрика, полностью поляризован в том случае, если тангенс угла падения численно равен относительному показателю преломления tgi1=n21, где n21 - показатель преломления второй среды (стекла) относительно первой (жидкости). Относительный показатель преломления равен отношению абсолютных показателей преломления. Следовательно,
![]()
Так как угол падения равен углу отражения, то i1=φ/2, и, следовательно,
![]()
откуда

Сделав подстановку числовых значений, получим:
![]()
Пример 28. На какой угол повернется плоскость поляризации света раствором сахара в стеклянной трубке длиной l = 20дм, концентрация которого составляет с = 0,2 г/см3? Удельное вращение для данного света
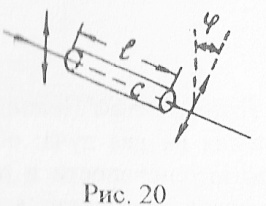
![]()
Дано: l = 20дм, с = 0,2 г/см3,
Найти: φ.
Р е ш е н и е . Плоскость колебаний поляризованного луча, проходящего через раствор сахара (рис. 20), поворачивается на угол, пропорциональный концентрации раствора с и длине трубки l, т.е.
![]()
где [φ0] - удельное вращение, показывающее, на какой угол поворачивается плоскость колебаний в растворе сахара единичной концентрации (с = 1г/см), при прохождении лучом расстояния в 1дм.
Подставляя в (1) числовые значения, получим
![]()
Угол поворота плоскости поляризации тоже ≈ 27°, так как она перпендикулярна плоскости колебаний.
Пример 29. Два николя N1, и N2 расположены так, что угол между плоскостями пропускания поляризаторов составляет α = 60°. Определить, во сколько раз уменьшится интенсивность I0 естественного света: 1) при прохождении через один николь N1; 2) при прохождении через оба николя. Коэффициент поглощения света в николе k = 0,05. Потери на отражение света не учитывать (рис.21).
Дано: α = 60°, k = 0,05.
Найти: I0/I1 , 10/12 .
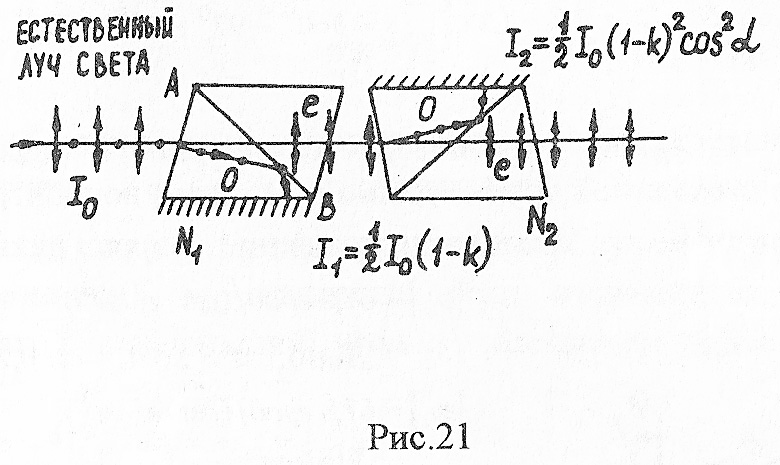
Р е ш е н и е . Естественный свет, падая на грань призмы Николя (рис.21), расщепляется вследствие двойного лучепреломления на два луча: обыкновенный и необыкновенный. Оба луча одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного луча лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного луча перпендикулярна плоскости чертежа. Обыкновенный луч О вследствие полного внутреннего отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч е проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, прошедшего через первую призму,
![]()
Относительное уменьшение интенсивности света получим, разделив интенсивность I0 естественного света, падающего на первый николь, на интенсивность I1, поляризованного света

Подставляя в (1) числовые значения, найдем
![]()
Таким образом, интенсивность уменьшится в 2,1 раза.
2. Плоско поляризованный луч света интенсивности I1 падает на второй николь N2 и также расщепляется на два луча различной интенсивности: обыкновенный и необыкновенный. Обыкновенный луч полностью поглощается призмой, поэтому его интенсивность нас не интересует. Интенсивность необыкновенного луча I2, вышедшего из призмы N2, определяется законом Малюса (без учета поглощения света во втором николе):
![]()
где α - угол между плоскостью колебаний в поляризованном луче и плоскостью колебаний, пропускаемых николем без ослабления. Учитывая потери на поглощение во втором николе, получим:
![]()
Искомое уменьшение интенсивности при прохождении света через оба николя найдем, разделив интенсивность I0 естественного света на интенсивность I2 света, прошедшего систему из двух николей
![]()
Заменяя
![]() его выражением по формуле (I),
получим:
его выражением по формуле (I),
получим:
![]()
Подставлял данные, произведем вычисления
![]()
Таким образом, после прохождения снега через два николя его интенсивность уменьшится в 8,86 раза.
Пример 30. Пластинку кварца толщиной d1=2мм поместили между
скрещенными поляроидами (поляризатором и анализатором), в результате чего плоскость колебаний поляризованного света повернулась на угол φ1=54° (рис.22). Какова должна быть толщина пластины d2, чтобы интенсивность вышедшего из анализатора света Iа равнялась интенсивности поляризованного света (поглощением света в системе пренебречь).
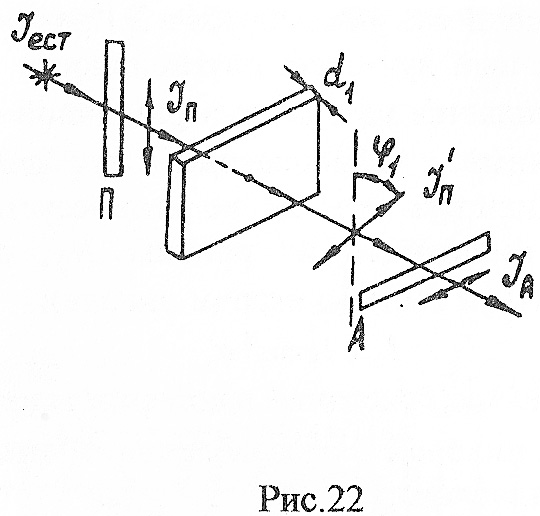
Дано: d1=2мм, φ1=54°, Iа = In.
Найти: d2 .
Р е ш е н и е . Интенсивности света, прошедшего через анализатор (Iа) и поляризатор (In), связаны законом Малюса Iа = In(cos2 φ). Поляроиды скрещены (угол между плоскостями их пропускания 90°), следовательно, без кварцевой пластинки Iа = 0, так как cos2 90° = 0. Чтобы интенсивности были равны (Iа = In) cos2 φ должен быть равен единице, а угол φ между плоскостью колебаний света, падающего на анализатор (In), и плоскостью пропускания анализатора должен быть равен нулю. Следовательно, пластинка кварца (d2) должна повернуть плоскость колебаний поляризованного луча (In) на угол
φ2 = 90°.
Чтобы найти постоянную вращения кварца [φ0], т.е. величину угла, на который поворачивается плоскость колебаний при прохождении каждого миллиметра толщины кварца, используем начальные условия: пластинка толщиной d1=2мм поворачивает плоскость колебаний на φ1 = 54°, отсюда
![]()
так как φ=[φ0]d .
Искомую толщину пластинки d2 найдем из соотношения:
![]()
Выполним проверку наименования результата:
![]()
Пример 31. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, λ0=0,58мкм (рис.23). Определить энергетическую светимость R поверхности тела.
Дано: λ0=0,58мкм = 0,58·10-6 м .
Найти: RЭ .
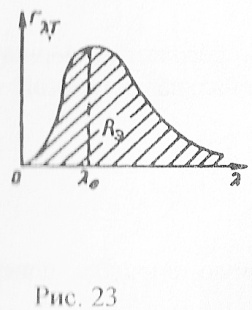
Р е ш е н и е . Энергетическая светимость R абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени абсолютной температуры и выражается формулой
![]()
где σ = 5,67·10-8 Вт/(м2К4) - постоянная Стефана-Больцмана; Т- абсолютная температура.
Температуру Т, входящую в формулу (1), можно вычислить с помощью закона смещения Вина
![]()
где с’=2,90∙10-3 мК - постоянная закона смещения Вина.
Выражая из формулы (2) температуру Т и подставляя ее в формулу (1),
имеем
![]()
Подставив числовые значения в формулу (3), получим:
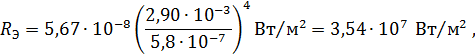
![]()
Выполним проверку наименования результата по формуле (3):

Пример 32. Серое тело, коэффициент поглощения которого аT = 0,3, излучает ежесекундно энергию W = 25Дж. Температура тела Т=2000К.
Определить величину излучающей поверхности.
Дано: аТ=0,3, t = 1c, W = 25 Дж, Т = 2000К.
Найти: S.
Р е ш е н и е . Энергетическая светимость серого тела
![]()
а на основании закона Кирхгофа в интегральной форме
![]()
Приравнивая правые части равенства (1) и (2), имеем
![]()
Откуда
![]()
Подставляя в (3) энергетическую светимость абсолютно черного тела, которая по закону Стефана-Больцмана пропорциональна четвертой степени температуры Rar=𝜎∙Т4, получим
![]()
где σ = 5,67∙10-8 Вт/(мК).
Подставив числовые значения, найдем искомую площадь поверхности серого тела:
![]()
Выполним проверку наименований результата по формуле (4):
![]()
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Решение задачи должно содержать три основных элемента: 1) краткую (буквенную) запись условия с исходными данными и переводом их в систему СИ (обязательный элемент решения для любых задач); 2) пронумерованные отдельные, независимые друг от друга исходные соотношения; 3) расчетную формулу.
Гармонические колебания материальной точки
Написать уравнение гармонического колебательного движения, если максимальное ускорение равно 49 см/с2, период 2 с и смещение в начальный момент времени равно 2,5 см. (Ответ: x = 0,005 · cos(π·t + π/ 3))
Амплитуда колебания математического маятника равна 2 см, его длина
1 м. Определить скорость в момент, когда ускорение равно 0,1 м/с2.
(Ответ:
υ
= ±
 = ±5.4·102
м/с.)
= ±5.4·102
м/с.)
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых в единицах СИ имеют вид x = 0,3 cos(π·t) и у = 0,4 sin (π·t). Найти уравнение траектории движения точки, начертить ее с соблюдением масштаба и указать направление движения точки по кривой. (Ответ:
 = 1 движение
происходит против часовой стрелки).
= 1 движение
происходит против часовой стрелки).
Материальная точка одновременно участвует в двух гармонических колебаниях, происходящих вдоль одной прямой. В единицах СИ уравнений слагаемых колебаний записываются в виде
X1 =0,5соs(π·t) ,
X2
=0,5cos(t+![]() )
)
Найти уравнение
результирующего колебания. (Ответ:
x
= 0,87·соs(π·t
+ ![]() )
)
Гармонические колебания абсолютно твердого тела.
Электромагнитные колебания
Однородный намагниченный стержень массой 60 г, длиной 10 см и магнитным моментом 4,9 А-м1 имеет горизонтальную ось вращения, проходящую через конец стрежня. Период гармонических колебаний стержня в однородном вертикальном магнитном поле в 2 раза меньше периода его собственных колебаний при отсутствии магнитного поля. Определить
индукцию
магнитного поля. (Ответ: B=
![]() =
1.8 ·
10-2
T)
=
1.8 ·
10-2
T)
Картонный диск радиусом 16 см подвесили на горизонтально расположенную ось, которая перпендикулярна плоскости диска и расположена на расстоянии 4 см от его центра, и вывели из положения равновесия.
Определить
период колебаний диска. (Ответ:
Т = 2
π ·
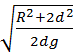 =1.21 с.)
=1.21 с.)
В колебательном контуре емкостью 4
 10-6
Ф и
индуктивностью 10-4
происходят
гармонические колебания. Найти
относительное изменение периода
колебаний в контуре при включении в
него сопротивления
2 Ом
10-6
Ф и
индуктивностью 10-4
происходят
гармонические колебания. Найти
относительное изменение периода
колебаний в контуре при включении в
него сопротивления
2 Ом
(Ответ:![]() =
=  ≈
≈ ![]() =0.02,
=0.02,
![]() )
)
Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами площадью 100 см2 каждая и катушки индуктивностью 10-6 Гн, резонирует на волну длиной 10 м. Определить расстояние между пластинами
конденсатора.
(Ответ: d
= ε0S(![]() )2·L
= 3,14 10-3
м = 3.14мм)
)2·L
= 3,14 10-3
м = 3.14мм)
Логарифмический декремент затухания колебаний маятники равен 0,003, Сколько полных колебаний должен сделать маятник, чтобы «амплитуда»
уменьшилась
в 2 раза? (Ответ:
N
= ![]() ln(A0/At
)=231.)
ln(A0/At
)=231.)
Вынуждающая сила, заданная в единицах СИ уравнением f(t)= 2sin(20t), действует на груз массой 0,2 кг, подвешенный на пружине. Коэффициент сопротивления 0,2 кг/с, коэффициент упругости пружины 2,0 Н/см. Определить уравнение установившихся вынужденных колебаний с числовыми коэффициентами. (Ответ: x(t) = 1,67· 10-2 sin(20t - 0,33))
Энергия механических и электромагнитных колебаний
Уравнение колебания материальной точки массой в 1 г в единицах СИ имеет вид х(t) = 0,2· sin π(t +
 ).
Определить кинетическую, потенциальную
).
Определить кинетическую, потенциальную
и полную энергии точки, момент времени t=l с.
(Ответ:
П = W0
sin(wt
+ α) = 14.8
Дж, Т = W
cos2
(
t
+ α) =
4,9·10
-4
Дж, W=![]() = 19.7 ·
10-5
Дж)
= 19.7 ·
10-5
Дж)
12.В
колебательном контуре происходят
гармонические колебания тока. В некоторый
момент времени электрическая энергия
конденсатора составляет одну четвертую
часть полной энергии. Определить
отношение величины тока к его амплитудному
значению в этот момент времени.
(Ответ: ![]() =
= ![]() = 0.87)
= 0.87)
Волны механические и электромагнитные
13.
Плоская звуковая волна, частота которой
100 Гц,
распространяется со скоростью 330
м/с в воздухе,
плотность которого равна 1,2
кг/м3.
Интенсивность
волны ![]() равна 2,0*10-3
Вт/м2.
Определить амплитуду колебаний. При
решении задачи учесть, что среднее
значение квадрата синуса (либо косинуса)
за период равно 0,5.
равна 2,0*10-3
Вт/м2.
Определить амплитуду колебаний. При
решении задачи учесть, что среднее
значение квадрата синуса (либо косинуса)
за период равно 0,5.
(Ответ:
A=
![]() ·
·![]() =5,05
10-6
м)
=5,05
10-6
м)
Для демонстрации опытов Герца с преломлением электромагнитных волн иногда берут большую призму, изготовленную из парафина. Определить показатель преломления парафина, если его диэлектрическая проницаемость
 = 2 и магнитная проницаемость
μ = 1. (Ответ:
п =
= 2 и магнитная проницаемость
μ = 1. (Ответ:
п =  = 1,41.)
= 1,41.)
Плоская электромагнитная волна, имеющая максимальную напряженность электрического поля 200 В/м, распространяется в среде, диэлектрическая проницаемость которой ε = 4, а магнитная проницаемость μ=1. Определить интенсивность волны. При решении задачи учесть, что среднее значение квадрата синуса (либо косинуса) за период равно 0,5. (Ответ: = 2 ·
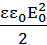 ·
υ
= 212
Вт/м2.)
·
υ
= 212
Вт/м2.)
16.
Уравнение колебаний источника в единицах
СИ имеет вид х
= 10-2
sin
2,5![]() ·t
.Найти смещение,
скорость и ускорение точки, находящейся
на расстоянии 20
м от источника
в момент времени t=1с.
Скорость распространения волны равна
100 м/с.
(Ответ: х =
0; υ=7,85
·10-2м/с;
а = 0.)
·t
.Найти смещение,
скорость и ускорение точки, находящейся
на расстоянии 20
м от источника
в момент времени t=1с.
Скорость распространения волны равна
100 м/с.
(Ответ: х =
0; υ=7,85
·10-2м/с;
а = 0.)
Интерференция и вопросы, связанные с ней.
На пути луча света поставлена стеклянная пластинка толщиной d=1мм так, что угол падения луча равен нулю. Определить изменение оптической длины пути луча. (Ответ : Δ
 =
d(n
-1)
= 0,5мм.)
=
d(n
-1)
= 0,5мм.)На мыльную плёнку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волны λ = 0,6мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина пленки?
(Ответ:![]() =
= ![]() = 0,113.)
= 0,113.)
Радиус второго темного кольца Ньютона в отраженном свете r2=0.4 мм
Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны λ=0.64 мкм.
(Ответ:
R=![]() ).
).
Дифракция, поляризация
20.На
пластину со щелью, ширина которой а=0,05
мм, падает
нормально монохроматический свет
длиной волны
λ = 0,7мкм.
Определить угол
![]() отклонения
лучей, соответствующих первому
дифракционному максимуму.
отклонения
лучей, соответствующих первому
дифракционному максимуму.
(Ответ:
1
=аrcsin![]() = 1°12'.)
= 1°12'.)
21.Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол = 30°. На какой угол отклоняет она спектр четвертого порядка?
(Ответ:
4
=аrcsin![]()
22.Угол преломления луча в жидкости i2 =35. Определить показатель n преломления жидкости, если известно, что отраженный луч максимально поляризован. (Ответ: п = tg(90° - i2) = 1,43 .)
23.На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10%?
(Ответ:
![]() )
)
ЭЛЕМЕНТЫ КВАНТОВОЙ И СТАТИСТИЧЕСКОЙ ФИЗИКИ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовыми лучами с длиной волны
λ = 0,155мкм.
Дано: λ = 0,155мкм =0,155·10-6 м
Найти. υmах .
Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта
Ε Φ = Aвых +Тmах, (1)
где Еф -энергия фотонов, падающих на поверхность металла; Τ -максимальная кинетическая энергия фотоэлектронов; Авых -работа выхода.
Энергия фотона вычисляется по формуле
Еф=![]() (2)
(2)
где h -постоянная Планка; с -скорость света в вакууме; λ -длина волны.
Кинетическая энергия электронов может быть выражена по классической формуле
T=![]() (3)
(3)
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия Еф фотона много меньше энергии покоя электрона, то может быть применена формула (3), если же Еф сравнима по величине с Е0, то вычисление по формуле (3) приводит к ошибке, во избежание которой необходимо кинетическую энергию фотоэлектрона выражать по формулам релятивистской механики.
Вычислим
энергию фотона ультрафиолетовых лучей
по формуле (2): Eф
=![]() Дж
Дж
или Еф
=![]() эВ
эВ![]() 8эВ.
8эВ.
Полученная энергия фотона (Еф = 8эВ) много меньше энергии покоя электрона (Е0=0,51MэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):
Eф=
А+![]()
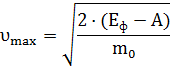
Зная, что А=4,7эВ=4,7·1,6·10-19Дж О,75·10-18 Дж, т0=9,11·10-31 кг, и подставляя числовые значения в формулу (4), найдем

Пример 2. В результате эффекта Комптона фотон при соударении с

электроном был рассеян на угол θ = 90° (рис.25). Энергия рассеянного фотона Е2ф=0.4 МэВ.
Определить энергию фотона Е1ф до рассеяния.
Дано θ =900, Е2ф=0.4 МэВ.
Найти: Е1ф.
Решение: Для определения энергии первичного фотона воспользуемся формулой Комптона:
Δλ=2![]() (1)
(1)
где Δλ= λ2
–λ1 -
изменение длины волны фотона в результате
рассеяния на свободном электроне; h-
постоянная Планка; ![]() – масса покоя электрона; с- скорость
света в вакууме; θ
– угол рассеяния фотона.
– масса покоя электрона; с- скорость
света в вакууме; θ
– угол рассеяния фотона.
Формулу
(1) преобразуем следующим образам:
1)заменим в ней Δλ на λ2-λ1;
2)выразим длины волн λ2
и λ1
через
энергии Е1ф
и
Е2ф
соответствующих
фотонов, воспользовавшись формулой
Еф=
![]() ;
3)умножим числитель и знаменатель
правой части формулы на с.
Тогда получим:
;
3)умножим числитель и знаменатель
правой части формулы на с.
Тогда получим:
![]()
Сократим на hc и выразим из полученной формулы искомую энергию

где Е0 =m0.c2 =0.51 MэВ – энергия покоя электрона.
Вычисления по формуле (2) удобнее вести во внесистемных единицах (МэВ):

Выполним проверку наименования результата по формуле (2):

Пример
3.
Параллельный пучок лучей с длиной волны
![]() = 0,5 мкм
падает нормально на зачерненную
поверхность, производя давление
= 0,5 мкм
падает нормально на зачерненную
поверхность, производя давление
Ρ = 105 Πа. Определить: а) концентрацию фотонов в потоке (число фотонов в единице объема), б) число фотонов, падающих на единицу площади в единицу времени.
Дано: = 0,5 мкм= 0,5· 10-6 м, ρ = 0, Ρ = 15 н/м2.
Найти: n0, n1.
Решение. а) Концентрация фотонов в потоке может быть найдена как частное от деления объемной плотности энергии w на энергию фотона Еф :
n0=![]() . (1)
. (1)
Величина объемной плотности энергии w связана с величиной светового давления соотношением
P = w· ( ρ +1), (2)
где ρ -коэффициент отражения.
Подставляя значение w из формулы (2) в формулу (1), получим
n0=
![]() (3)
(3)
Энергия фотона зависит от частоты ν, а следовательно, и от длины световой волны λ:
Еф
=h![]() v
=
v
=
где с =3 108 м/с -скорость света в вакууме; h -постоянная Планка, равная
6,63 10-34 Дж с.
Внося выражение для энергии фотона в формулу (3), получим искомую концентрацию фотонов
n0
= ![]() · (4)
· (4)
Подставляя в (4) значения приведенных величин, получим:
n0=![]() м-3
м-3
б) Если плотность потока энергии J, т.е. энергию, падающую в единицу
в
(5)![]() ,
получим число фотонов
,
получим число фотонов ![]() ,
падающих на единицу площади в единицу
времени:
,
падающих на единицу площади в единицу
времени:
![]()
П
(6)
![]()
Подставляя (6) в формулу (5), будем иметь
![]()
или, выражая объемную плотность энергии через давление согласно (2), получим
![]()
С
(7)
![]()
Подставляем в (7) числовые значения:
![]()
Выполним проверку наименований результатов по формулам (4) и (7):
![]()
![]()
Пример 4. Электрон в атоме водорода перешел с четвертого уровня на второй. Определить энергию испущенного при этом фотона.
Дано:
![]()
Найти:
![]() .
.
(1)

где
![]() – длина волны фотона; R
– постоянная Ридберга; Z
– заряд ядра в относительных единицах
(при Z=1
формула переходит в сериальную формулу
для водорода);
– длина волны фотона; R
– постоянная Ридберга; Z
– заряд ядра в относительных единицах
(при Z=1
формула переходит в сериальную формулу
для водорода); ![]() главное
квантовое число уровня, на который
перешел электрон;
главное
квантовое число уровня, на который
перешел электрон; ![]() главное квантовое число уровня, с
которого перешел электрон. Умножив обе
части равенства (1) на
главное квантовое число уровня, с
которого перешел электрон. Умножив обе
части равенства (1) на ![]() ,
получим выражение для энергии излучаемого
фотона:
,
получим выражение для энергии излучаемого
фотона:

Так
как величина ![]() есть энергия ионизации
есть энергия ионизации ![]() атома водорода, то
атома водорода, то
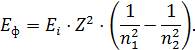
Вычисления
выполним во внесистемных единицах: ![]() эВ (см. справочную табл. 1); Z=1
(заряд ядра атома водорода в относительных
единицах, где за единицу заряда принято
абсолютное значение заряда электрона);
эВ (см. справочную табл. 1); Z=1
(заряд ядра атома водорода в относительных
единицах, где за единицу заряда принято
абсолютное значение заряда электрона);
![]()
![]()
Пример
5. Электрон,
начальной скоростью которого можно
пренебречь, прошел ускоряющую разность
потенциалов ![]() .
Найти длину волны де Бройля для электрона.
.
Найти длину волны де Бройля для электрона.
Дано:
![]()
Найти:
![]()
Р
(1)
![]()
г
(2)![]() частицы. В данном случае она равна
работе сил электрического поля над
зарядом
частицы. В данном случае она равна
работе сил электрического поля над
зарядом
![]()
С
другой стороны, связь импульса и
кинетической энергии различна для
релятивистской (![]() )
и нерелятивистской частицы (
)
и нерелятивистской частицы (![]() ).
В последнем случае
).
В последнем случае
![]()
и
(3)
![]()
Комбинируя формулы (2) и (3), получим из (1)
![]()
Вычисления:
![]()
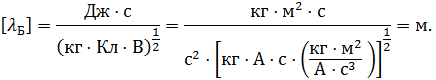
Пример
6. Излучение
возбужденного атома происходит в
течение времени ![]() .
Определить, с какой наибольшей
относительной точностью
.
Определить, с какой наибольшей
относительной точностью ![]() может быть найдена энергия излучения,
если его частота
может быть найдена энергия излучения,
если его частота ![]() Гц.
Гц.
Дано:
![]()
Найти:
![]()
Р
(1)
![]()
В
(2)
![]()
(Заметим,
что ![]() или через малые изменения
или через малые изменения![]() ).
).
Разделив
правую и левую части формулы (1) и (2) и
учитывая, что можно положить![]() ,
получим:
,
получим:
![]()
Откуда ![]()
Вычисления:
![]()
 Пример
7. Волновая
функция
Пример
7. Волновая
функция ![]() описывает
основное состояние частицы в бесконечно
глубоком прямоугольном ящике шириной
описывает
основное состояние частицы в бесконечно
глубоком прямоугольном ящике шириной
![]() .
Вычислить вероятность нахождения
частицы в малом интервале
.
Вычислить вероятность нахождения
частицы в малом интервале ![]() в двух случаях:
в двух случаях:
1)вблизи
стенки ![]() ;
;
2)
в средней части ящика (рис. 26): ![]()
Дано:
![]()
Найти:
![]() при
при ![]() ;
; ![]() при
при
Р
е ш е н и е. Вероятность того, что частица
будет обнаружена в интервале ![]() ,
пропорциональна этому интервалу и
квадрату модуля волновой функции,
описывающей данное состояние:
,
пропорциональна этому интервалу и
квадрату модуля волновой функции,
описывающей данное состояние:
![]()
В
первом случае искомая вероятность
найдется интегрированием в пределах
от 0 до ![]() (рис. 26).
(рис. 26).

Знак
модуля опущен, так как ![]() – функция в данном случае не является
комплексной.
– функция в данном случае не является
комплексной.
Так
как ![]() изменяется в интервале
изменяется в интервале ![]() и, следовательно,
и, следовательно, ![]() ,
справедливо приближенное равенство
,
справедливо приближенное равенство
![]()
С учетом этого выражения (1) примет вид:

После интегрирования получим:
![]()
Во
втором случае можно обойтись без
интегрирования, так как квадрат модуля
волновой функции вблизи ее максимума
в заданном малом интервале ![]() практически не изменяется. Искомая
вероятность во втором случае определяется
выражением
практически не изменяется. Искомая
вероятность во втором случае определяется
выражением
![]()
Пример
8. Определить
ширину
потенциального ящика для электрона с
бесконечно высокими стенками, если для
перехода из 2-го в 3-ье энергетическое
состояние ему необходимо сообщить
энергию ![]() .
.
Дано:
n![]()
Найти:
![]()
Р е ш е н и е. Энергия n-го энергетического состояния электрона в потенциальном ящике с бесконечно высокими стенками находится из решения стационарного уравнения Шредингера для волновой функции электрона :
![]()
В
ящике, где потенциальная энергия частицы
![]() ,
уравнение (1) имеет вид:
,
уравнение (1) имеет вид:
![]()
или
![]()
при
![]()
Решение
последнего уравнения (2), с учетом
граничных условий ![]() является действительной функцией
является действительной функцией

где
![]() определяет
значение энергии n-го
уровня
определяет
значение энергии n-го
уровня
![]()
Разность энергий между соседними уровнями
![]()
Отсюда находим исходную ширину потенциального ящика

Вычисления:

Пример
9. Найти
среднюю квадратичную скорость молекул
кислорода, если внутренняя энергия 0,2
молей газа равна 1660 Дж.
Найти среднюю энергию поступательного
![]() и вращательного
и вращательного ![]() движений одной молекулы.
движений одной молекулы.
Дано:
![]()
Найти:
![]()
Р е ш е н и е. Внутренняя энергия идеального газа при заданной температуре определяется выражением
![]()
где i – число степеней свободы, соответственно равное 3, 5 или 6 для одно-, двух-, или трехатомных молекул, R – универсальная газовая постоянная. Из формулы (1) сразу получаем значение абсолютной температуры газа
![]()
(2)![]() одной частицы равна сумме кинетических
энергий поступательного и вращательного
движений
одной частицы равна сумме кинетических
энергий поступательного и вращательного
движений
![]()
где
для двухатомного кислорода ![]()
(3)
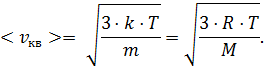
Здесь m – масса одной частицы, k – постоянная Больцмана.
П
(4)
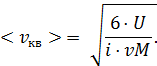
Вычисления:

![]()
![]()
![]()

Пример 10. Исходя из максвелловского распределения молекул идеального газа по энергии, определить наиболее вероятное значение их энергии.
Дано:
![]()
Найти:
![]()
Р
е ш е н и е. Среднее число частиц, энергии
которых лежат в интервале ![]()
![]()
причем
![]() – распределение Максвелла по энергии.
Наиболее вероятное значение
– распределение Максвелла по энергии.
Наиболее вероятное значение ![]() определяем из условия экстремума
функции F(E),
т.е. при
определяем из условия экстремума
функции F(E),
т.е. при ![]()
Дифференцируя F(E) и сокращая постоянные множители, имеем
![]()
![]() и окончательно имеем
и окончательно имеем ![]()
Пример 11. Зная распределение Максвелла молекул идеального газа по скоростям, получить для них аналогичное распределение по импульсам. Показать, что среднее значение проекции импульса частицы равно нулю.
Дано:
![]()
Найти:
![]()
Р
е ш е н и е. Функция распределения частиц,
скорости которых лежат в интервалах
![]() равна
равна
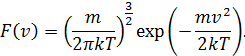
В силу принципа мультипликативности
![]()
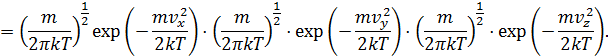
Число частиц в заданных интервалах проекций скоростей

и,
учитывая далее, что ![]() ,
и, соответственно
,
и, соответственно ![]() ,
,
![]() где
где ![]() или z,
получим, переходя к новым переменным:
или z,
получим, переходя к новым переменным:
![]()

или

Среднее
значение одной из проекций импульса
найдем, используя ![]() :
:


где
![]()
Пример
12. Считая
газ идеальным, найти изменение энтропии
4,8 г азота при расширении его от объема
20 л до 54 л при температуре ![]() .
.
Дано:
![]()
![]()
Найти:
![]()
Р
(1)

г
(2)
![]()
причем
![]() – давление газа,
– давление газа, ![]() – молярная теплоемкость.
– молярная теплоемкость.
Выражая
давление из уравнения состояния ![]() и подставляя в соотношение (2), для
интеграла (1) получим
и подставляя в соотношение (2), для
интеграла (1) получим

Переходя к конкретным пределам интегрирования, запишем

Вычисления:


Пример
13. Найти
изменение энтропии 5,56 кг льда, взятого
при температуре ![]() ,
при превращении его полностью в воду.
Удельная теплоемкость плавления льда
,
при превращении его полностью в воду.
Удельная теплоемкость плавления льда
![]()
Дано:
![]() .
.
Найти:
(1)

При плавлении массы dm требуется затратить при неизменной температре количество теплоты
![]()
Тогда:

Вычисления:
![]()
![]()
Пример
14. Вычислить
максимальную энергию ![]() , которую могут иметь свободные электроны
в металле (медь) при абсолютном нуле.
Принять, что на каждый атом меди
приходится по одному электрону.
, которую могут иметь свободные электроны
в металле (медь) при абсолютном нуле.
Принять, что на каждый атом меди
приходится по одному электрону.
Р
е ш е н и е. Максимальная энергия
, которую могут иметь электроны в металле
при абсолютном нуле, равна энергии
Ферми ![]() , связана с концентрацией свободных
электронов соотношением
, связана с концентрацией свободных
электронов соотношением
![]()
где
![]() - постоянная Планка, деленная на 2
- постоянная Планка, деленная на 2![]() ,
m
– масса электронна.
,
m
– масса электронна.
Концентрация свободных электронов, по условию задачи, равна концентрации атомов, которая может быть найдена по формуле
![]()
где
![]() – плотность меди;
– плотность меди; ![]() – число Авогадро;
– число Авогадро; ![]() – молярная масса. Подставляя выражение
концентрации в формулу (1), получим
– молярная масса. Подставляя выражение
концентрации в формулу (1), получим

Подставим числовые значения величин, входящих в последнюю формулу, и произведем вычисления:
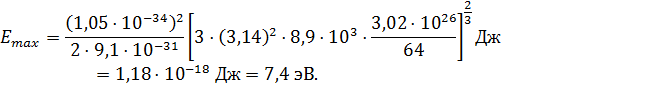
Замечание:
величина
,
называемая про T=0K
энергией Ферми или уровнем Ферми, в
ряде пособий обозначается буквами
![]() или
или
![]() .
.
Пример
15. Считая,
что на каждый атом калия приходится
один свободный электрон, с эффективной
массой ![]() ,
найти значение энергии Ферми для калия
при температуре
,
найти значение энергии Ферми для калия
при температуре ![]() .
Учесть, что масса атома К в относительных
единицах массы М=39,1 , его плотность
.
Учесть, что масса атома К в относительных
единицах массы М=39,1 , его плотность ![]()
Дано:
металлический калий К; ![]()
Найти:
![]()
(1)

г
(2)![]() – энергия Ферми при Т=0
– энергия Ферми при Т=0

Здесь h – постоянная Планка, m – эффективная масса электрона, n – концентрация свободных электронов в металле, равная числу атомов в единице объема
![]()
Вычисления:


Видно, что при невысоких температурах химический потенциал практически совпадает с .
Пример
16. Определить
долю свободных электронов металла при
абсолютном нуле, энергия которых
заключена в интервале от ![]() до
.
до
.
Р е ш е н и е. Распределение электронов по энергиям (распределение Ферми-Дирака) имеет вид:

где
d
n(E)
– концентрация электронов в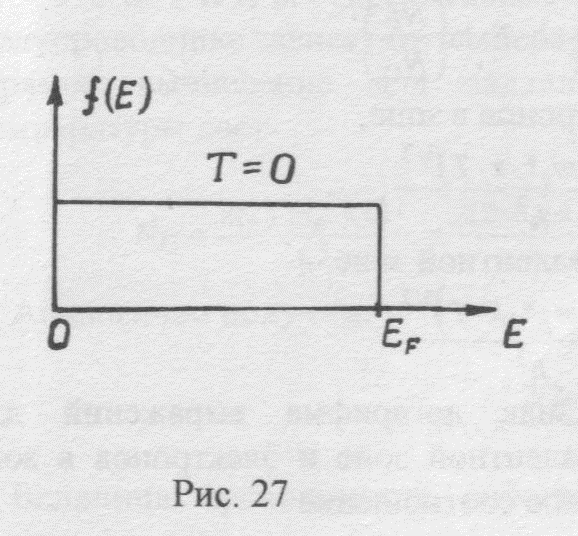 интервале энергий Е, Е+dE.
Известно, что функция Ферми
интервале энергий Е, Е+dE.
Известно, что функция Ферми ![]() имеет следующие значения при T=0:
имеет следующие значения при T=0:
при
![]()
![]() ,
,
при
![]()
![]()
(график на рис.27).
Таким образом, распределение Ферми-Дирака при T=0 упрощается:
![]() .
.
Концентрацию
электронов с энергиями в указанном
интервале находят, интегрируя ![]() :
:

Выражая
через n
согласно формуле (2) примера 15, находят
![]() Для искомой величины получаем
Для искомой величины получаем ![]()
Пример
17. На сколько
и куда смещено положение уровня
химического потенциала в кремнии при
T=300К,
если считать, что эффективные массы
электрона и дырки соответственно равны
![]() ?
Ширина запрещенной зоны в Si
?
Ширина запрещенной зоны в Si
![]()
Дано:
![]()
Найти:
![]()
Р
е ш е н и е. Важнейшим обстоятельством,
отличающим полупроводники от металлов,
является отсутствие у первых свободных
носителей заряда при Т=0. С повышением
температуры концентрация электронов
в зоне проводимости растет как и
концентрация дырок в валентной зоне.
Для случая малых чисел заполнения ![]() поведение носителей определяется
классическим распределением
Максвелла-Больцмана
поведение носителей определяется
классическим распределением
Максвелла-Больцмана
![]()
Для
собственного проводника при Т=0 ![]() находится точно в середине запрещенной
зоны:
находится точно в середине запрещенной
зоны: ![]() .
Однако при
.
Однако при ![]()
![]()
где
![]() – эффективное число состояний электронов
в зоне,
– эффективное число состояний электронов
в зоне,

![]() – эффективное число состояний дырок
в валентной зоне,
– эффективное число состояний дырок
в валентной зоне,

Причем, после подстановки под знак логарифма выражений для эффективных чисел состояний дырок в валентной зоне и электронов в зоне проводимости, оно переходит в эквивалентное соотношение

С
учетом того, что ![]() ,
а постоянная Больцмана
,
а постоянная Больцмана ![]() , непосредственный расчет дает
, непосредственный расчет дает ![]() .
.
Так
как при T
= 0К, ![]() ,
очевидно, что уровень химического
потенциала сдвинут к потолку валентной
зоны на величину
,
очевидно, что уровень химического
потенциала сдвинут к потолку валентной
зоны на величину ![]() .
.
Пример
18. Найти
эффективные числа состояний для
электронов в зоне проводимости и дырок
в валентной зоне Ge
при T
= 287K
в предположении, что ![]() и
и ![]() .
Чему равна плотность тока проводимости
при этой температуре и напряженности
электрического поля
.
Чему равна плотность тока проводимости
при этой температуре и напряженности
электрического поля![]() ?
Ширина запрещенной зоны
?
Ширина запрещенной зоны ![]() ,
подвижности носителей заряда
,
подвижности носителей заряда ![]() и
и ![]() .
.
Дано:
![]()
![]()
Найти:
![]()
Р е ш е н и е. Эффективные числа состояний для электрона и дырки в полупроводнике зависят от температуры и эффективных масс носителей заряда. Прямое вычисление для заданных значений параметров кристалла и температуры дает
![]()
Аналогично получим:
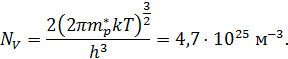
Величина
проводимости собственного полупроводника
выражается через
(1)![]() и дырок
и дырок ![]() ,
концентрации носителей
,
концентрации носителей ![]() и
и ![]() ,
их заряд, равный по модулю заряду
электрона:
,
их заряд, равный по модулю заряду
электрона:
![]()
Так
как в условиях равновесия эти концентрации
равны ![]() и определяются соотношением
и определяются соотношением
![]()
то,
используя значения
и
и учитывая, что ![]() ,
получим
,
получим

Подставляя эту величину в выражение (1), найдем
![]()
В соответствии с законом Ома в дифференциальной форме, плотность тока будет равна
![]()
Проверка размерностей:

![]()
![]()
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Фотон и его характеристики. Фотоэффект и эффект Комптона.
Определить энергию , массу m, импульс P фотона с длиной волны
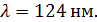
(Ответ:
![]()
![]()
![]()
На пластинку падает монохроматический свет (
 ).
Фототок прекращается при задерживающей
разности потенциалов
).
Фототок прекращается при задерживающей
разности потенциалов 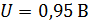 .
Определить работу А
выхода электронов с поверхности
пластины.
.
Определить работу А
выхода электронов с поверхности
пластины.
(Ответ:
![]() ).
).
На цинковую пластину падает пучок ультрафиолетовых лучей (
 ).
Определить максимальную кинетическую
энергию
).
Определить максимальную кинетическую
энергию  и максимальную скорость
и максимальную скорость  фотоэлектронов.
фотоэлектронов.
(Ответ:
![]() ;
; ![]() ).
).
Определить угол
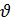 рассеяния фотона, испытывающего
соударения со свободным электроном,
если изменение его длины волны при
рассеянии
рассеяния фотона, испытывающего
соударения со свободным электроном,
если изменение его длины волны при
рассеянии  .
.
(Ответ:
![]()
![]() ).
).
Фотон с энергией
 ,
равной энергии покоя электрона (
,
равной энергии покоя электрона ( ),
рассеялся на свободном электроне на
угол
),
рассеялся на свободном электроне на
угол  .
Определить энергию
.
Определить энергию 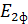 рассейнного фотона и кинетическую
энергию T
фотона отдачи (в единицах
рассейнного фотона и кинетическую
энергию T
фотона отдачи (в единицах  ).
).
(Ответ:
![]()
![]() ).
).
Параллельный пучок монохроматических лучей с длиной волны
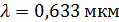 падает на зачерненную поверхность и
производит на неё давление
падает на зачерненную поверхность и
производит на неё давление 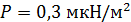 .
Определить концентрацию n
фотонов в световом пучке.
.
Определить концентрацию n
фотонов в световом пучке.
(Ответ:
![]() ).
).
Движение электрона в атоме, ионизация.
Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной.
(Ответ:
![]() ).
).
Определить первый потенциал возбуждения атома водорода.
(Ответ:
![]() ).
).
Исходя из представлений Бора, вычислить радиус четвертой орбиты электрона в атоме лития, потерявшем два электрона, а также скорость электрона на этой орбите.
(Ответ:
![]() ;
; ![]() ).
).
Из атома водорода, находящемся в третьем энергетическом состоянии, в результате поглощения фотона вылетает электрон, кинетическая энергия которого вдали от ядра равна 2 эВ. Определить энергию фотона (в электрон-вольтах).
(Ответ:
![]() ).
).
Длина волны де Бройля. Электрон в потенциальном ящике.
Вычислить длину волны де Бройля для электрона, прошедшего ускоряющую разность потенциалов
 .
.
(Ответ:
![]() ).
).
Электрон находится в прямоугольном потенциальном ящике с непроницаемыми стенками. Ширина ящика
 ,
энергия электрона в ящике
,
энергия электрона в ящике 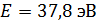 .
Определить номер n
энергетического уровня и значение
волнового числа k.
.
Определить номер n
энергетического уровня и значение
волнового числа k.
(Ответ:
![]() ;
; ![]() ).
).
Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружить частицу в крайней трети ящика?
(Ответ:
![]() ).
).
Статистическая физика
Найти изменение энтропии 9 г паров воды при изотермическом расширении от объема 18л до объема 48,6л.
(Ответ:
![]() ).
).
Металл находится при абсолютном нуле. Определить относительное число электронов, энергии которых отличаются от энергии Ферми не более чем на 2%.
(Ответ:
![]() ,
учитываем, что
,
учитываем, что ![]() ).
).
КОНТРОЛЬНАЯ РАБОТА №2
Студент должен решить шесть задач того варианта, номер которого совпадает с последней цифрой его шифра (номера студенческого билета). Решение задач, отмеченных звёздочкой, обязательно сопровождать рисунками.
вариант |
Номера задач |
|||||
1 |
201 |
211 |
221 |
231* |
241* |
251* |
2 |
202* |
212 |
222 |
232* |
242 |
252* |
3 |
203 |
213* |
223 |
233* |
243 |
253* |
4 |
204* |
214 |
224 |
234* |
244* |
254* |
5 . |
205 |
215 |
225 |
235* |
245* |
255* |
6 |
206* |
216 |
226 |
236* |
246 |
256* |
7 |
207* |
217* |
227 |
237* |
247 |
257* |
8 |
208 |
218 |
228 |
238* |
248 |
258* |
9 |
209* |
219 |
229 |
239* |
249 |
259* |
10 |
210 |
220 |
230 |
240* |
250 |
250* |
201. Тело массой m=48 г совершает затухающие колебания на пружине, погруженной в вязкую жидкость. Найти коэффициент сопротивления среды r, если за 2,5 с колебательная система теряет 80% своей энергии. Определить, через какое время амплитуда смещения тела уменьшается в е = 2,718 раз.
202*. Груз массой 360 г колеблется в масле на пружине с жёсткостью
k=
0,568 Н/см. Сила сопротивления пропорциональна
и противоположна по направлению
скорости груза. Считая, что коэффициент
пропорциональности r
=1.44 ![]() ,
составить на основе 2-го закона Ньютона
дифференциальное уравнение колебаний
груза, записать его решение в общем
виде и с числовыми коэффициентами.
Найти циклическую частоту и период
затухающих колебаний.
,
составить на основе 2-го закона Ньютона
дифференциальное уравнение колебаний
груза, записать его решение в общем
виде и с числовыми коэффициентами.
Найти циклическую частоту и период
затухающих колебаний.
203.
Добротность Θ последовательного L-R-С
контура составляет 26,17. Через сколько
полных колебаний амплитуда напряжения
уменьшится в 11 раз? Считая, что период
затухающих колебаний ![]() =
5мс, записать закон убыли амплитуды
в общем виде, используя упомянутые
параметры.
=
5мс, записать закон убыли амплитуды
в общем виде, используя упомянутые
параметры.
204*. Колебательный контур с сопротивлением R=40 Ом и индуктивностью 0,001 Гн содержит батарею из 10 последовательно соединённых конденсаторов, ёмкость каждого из которых 0,8 мкФ. Определить период и логарифмический декремент затухающих колебаний в контуре. Найти значение критического сопротивления, при котором процесс станет апериодическим.
205*. Полная энергия электрического колебательного контура, содержащего последовательно соединённые катушку с индуктивностью 1,8 мГн, конденсатор и активное сопротивление, за t = 0,2 мс уменьшилась в 80 раз. Найти активное сопротивление этого контура. Во сколько раз изменится амплитуда колебаний напряжения в таком контуре за вдвое меньшее время?
206. За 100 с система успевает совершить 100 колебаний. За то же время амплитуда колебаний уменьшается в 2,718 раз. Чему равна относительная убыль энергии системы ΔЕ/E за период колебаний? Какова добротность колебательной системы?
207*. Последовательный электрический контур содержит две катушки индуктивности L1=0,05 Гн и L2=0,075 Гн, разделённых ёмкостью С=0,02 мкФ и сопротивлением R=800 Ом, также соединённых последовательно. Исходя из 2- го закона Кирхгофа, составить дифференциальное уравнение колебаний электрического заряда, записать его решение и определить циклическую частоту и период затухающих колебаний. Определить время, за которое энергия электрического поля конденсатора уменьшится в 7,34 раза.
208. Найти добротность маятника, представляющего собой маленький шарик, подвешенный на длинной нити l = 0,5 м, если за время наблюдения t=1,5 мин его полная механическая энергия уменьшилась в n=36 раз. Различием частот собственных и затухающих колебаний пренебречь.
209*. Пользуясь условием задачи № 306* и считая, что момент сил сопро-
тивления
Мс
= -r![]() ,
где г = 3 ·
10-7
,
где г = 3 ·
10-7
![]() коэффициент пропорциональности,
коэффициент пропорциональности,
= ![]() - угловая скорость колебаний ωкол,
составить дифференциальное
- угловая скорость колебаний ωкол,
составить дифференциальное
уравнение колебаний стержня, записать его решение, найти период затухающих колебаний, циклическую частоту и постоянную времени релаксации процесса.
210*. Номинальные значения параметров последовательного электрического L-R-C контура таковы: L=0,04 Гн, R=250 Ом. Добротность контура Θ=80. Найти время релаксации колебаний в системе и значение сопротивления, при котором наступает критический режим колебаний.
211.Амплитуды и периоды двух одинаково направленных гармонических колебаний равны, фазы же различаются на 2π/3. Уравнение результирующего колебания в единицах СИ имеет вид x= 0,2cos(π·t+ π ). Определить уравнение слагаемых колебаний.
212. В последовательном R-L-C контуре действует периодическая ЭДС - ε(t)=ε0·cos(ωt). Значение параметров элементов системы: L=1,25·10-2Гн, С=2·10-7Ф, R=25 Ом. Определить максимальную величину амплитуды напряжения на конденсаторе и её значение при частоте ω = 0,8 ωрез, если амплитуда ЭДС εо=12 В.
213*. На подвешенный к пружине груз массой 0.1 кг действует вынуждающая сила с амплитудой 0,4 Н. Коэффициент сил сопротивления среды равен 0,3 кг/с, коэффициент упругости пружины 4 Н/м. Найти частоту колебаний вынуждающей силы, при которой в системе наступает резонанс, и величину амплитуды при резонансе. Записать дифференциальное уравнение колебаний груза и его решение в установившемся режиме.
214. Вынуждающее напряжение, действующее в колебательном контуре (в единицах СИ), имеет вид U(t) = 40cos(104 π·t). Индуктивность контура 10-5 Гн, емкость 10-5 Ф, сопротивление 0,2 Ом. Определить уравнение установившихся колебаний заряда на обкладках конденсатора с числовыми коэффициентами и записать дифференциальное уравнение, описывающее указанные колебания.
215*. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых в единицах СИ имеют вид x = 0,4cos π·t и y= 0,2 cos π(t - 0,5). Определить траекторию движения точки и начертить её с соблюдением масштаба. Рассчитать и указать на чертеже скорость и ускорение точки в начальный момент времени и указать направление её движения по кривой. Если траектория не замкнутая, то указать пределы движения.
216*. Материальная точка участвует одновременно в двух гармонических колебаниях, происходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x1 =0,1cosπ(t + 1/6) и
х2 = 0,05cosπ(t + 1/2). Определить уравнение результирующих колебаний.
217*. Определить добротность L-R-C последовательного электрического контура, содержащего периодическую эдс, если индуктивность катушки
L =2,5 Гн, активное сопротивление контура R = 12,5 Ом, а максимальное значение напряжения на резисторе Um = 50 В достигается при частоте ν= 9,28 Гц. Считать затухание малым. Определить резонансную амплитуду колебаний силы тока. Записать дифференциальное уравнение колебаний заряда на обкладках конденсатора и его решение в установившемся режиме.
218*. Пользуясь условием задачи № 326, получить ответы, считая, что уравнения движения материальной точки имеют вид: x1=0,lcosπ·t/2 и х2 = 0,12cosπ(t +1)/2.
219. Вынуждающая сила, заданная в единицах СИ уравнением F(t) = l,5sin 20t, действует на груз массой 0,3 кг, подвешенный на пружине. Коэффициент сопротивления среды 0,18 кг/с, коэффициент упругости пружины 2,5 Н/см. Записать уравнение установившихся вынужденных колебаний с числовыми коэффициентами и указать, решением какого дифференциального уравнения оно является.
220. Математический маятник длиной 80 см в начальный момент имеет максимальную скорость, равную 28 см/с. Определить уравнение гармонических колебаний маятника. Записать дифференциальные уравнения колебаний для углового смещения.
221*. Плоская электромагнитная волна, имеющая максимальную напряженность электрического поля 20 в/м и частоту 106 Гц, распространяется в вакууме. Определить уравнения электромагнитной волны с числовыми коэффициентами, выбрав произвольно начальные условия. Найти интенсивность волны. Привести снимок и осциллограмму подобной волны.
222. От источника колебаний с частотой 100 Гц вдоль прямой распространяется волна со скоростью 330 м/с и амплитудой 0,50 мкм. Определить длину волны, фазу и ускорение колебаний точки, удаленной на 0,33 м от источника колебаний в тот момент, когда от начала колебаний источника прошло 0,004 с. Колебания происходят по закону синуса; начальная фаза колебаний источника равна нулю.
223. Плоская электромагнитная волна, имеющая амплитуду напряженности электромагнитного поля 0,150 В/м, распространяется в вакууме. Определить энергию, проносимую волной за 2 с сквозь расположенную перпендикулярно к направлению распространения волны площадку 10 см2. При решении задачи следует учесть, что среднее значение квадрата синуса (либо косинуса) за период равно 0,5.
224. Вдоль стального стержня, плотность которого 7,8 г/см, распространяется продольная упругая волна со скоростью 5·103м/с. Амплитуда колебаний равна 1 мкм, длина волны 5м. Определить максимальное значение плотности потока энергии.
225. Излучаемая точечным источником сферическая электромагнитная волна, уравнение которой в системе СИ имеет вид :
E(r,
t) =
![]()
H(r,t)
=
![]() sin(6·
106π·
t-
0,02π·r)
,
sin(6·
106π·
t-
0,02π·r)
,
распространяется в вакууме. Определить среднюю мощность источника электромагнитной волны. При решении задачи следует учесть, что среднее значение квадрата синуса за период равно 0,5.
226. Плоская электромагнитная волна, уравнения которой в единицах СИ
имеют вид: Е(x,t) =140 · sin(6 ·106·t — 0,02π · х),
Н (х, t) = 0,37 · sin(6 ·106π·t — 0,02π · х),
распространяется
в вакууме. Определить среднюю мощность,
проходящую сквозь перпендикулярно
расположенную к направлению распространения
волны площадку 10 ![]() . При решении задачи следует учесть,
что среднее значение квадрата синуса
за период равно 0,5.
. При решении задачи следует учесть,
что среднее значение квадрата синуса
за период равно 0,5.
227. Плоская звуковая волна, уравнение которой в единицах СИ имеет вид:
y(x,t)=2.5·![]() распространяется
в воздухе, плотность которого
0,0012 г/см .
Определить энергию, проносимую волной
за одну минуту сквозь площадку 12 см2,
перпендикулярно распространению волны.
При решении задачи следует учесть, что
среднее значение квадрата синуса за
период равно 0,5.
распространяется
в воздухе, плотность которого
0,0012 г/см .
Определить энергию, проносимую волной
за одну минуту сквозь площадку 12 см2,
перпендикулярно распространению волны.
При решении задачи следует учесть, что
среднее значение квадрата синуса за
период равно 0,5.
228. Плоская электромагнитная волна, интенсивность которой равна 12 Вт/м2, распространяется в вакууме. Частота колебаний волны 2·106 Гц. Определить уравнения электромагнитной волны с числовыми коэффициентами, произвольно выбрав начальные условия. При решении задачи следует учесть, что среднее значение квадрата синуса (либо косинуса) за период равно 0,5.
229. Плоская электромагнитная волна, имеющая амплитуду напряженности электрического поля 0,12B/м, распространяется в среде, диэлектрическая проницаемость которой ε = 2 и магнитная проницаемость μ=1. Определить уравнения электромагнитной волны с числовыми коэффициентами, произвольно выбрав начальные условия. Частота волны равна 105 Гц. Определить среднее значение вектора Пойнтинга.
230. Плоская звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со скоростью 300 м/с в воздухе, плотность которого равна
1,2 кг/м3 . Определить интенсивность волны. При решении задачи следует учесть, что среднее значение квадрата синуса (либо косинуса) за период равно 0,5.
231*. На сколько изменится расстояние между максимумами яркости смежных интерференционных полос на экране наблюдения интерференционной картины в опыте Юнга, составляющее 1,2 мм, если фиолетовый светофильтр (λ = 0,44мкм) заменить красным (λ = 0,66мкм) ?
232*. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей с длиной волны λ= 147 пм. Расстояние между атомными плоскостями кристалла d = 280 пм. Под каким углом φ к плоскости грани наблюдается дифракционный максимум второго порядка?
233*. На дифракционную решетку, постоянная которой d = 2,4 мкм, падает нормально параллельный пучок белого света. Спектры второго и третьего порядка частично накладываются друг на друга. На какую длину волны в спектре второго накладывается фиолетовая граница (λ = 400нм) спектра третьего порядка? Под каким углом к оптической оси прибора это наблюдается?
234*. На непрозрачную пластинку с круглым отверстием диаметром d= 1,0 мм падает нормально плоская волна монохроматического света. На пути лучей, прошедших через отверстие, помещают экран. Максимальное расстояние от пластинки до экрана, при котором в центре дифракционной картины ещё наблюдается темное пятно Lmax = 25 см. Найти длину волны падающего света.
235*. Определить расстояние между третьей и шестой соседними интерференционными полосами (минимумами) в опыте Юнга, если узкие щели, расстояние между которыми 0,8 мм, освещаются монохроматическим светом с длиной волны 480 нм, а расстояние до экрана наблюдения равно 1,6м.
236*. Светло или темно будет в точке экрана наблюдения дифракционной картины для лучей, отклоняющихся под углом 30° при нормальном падении света с длиной волны 0,6 мкм на узкую щель шириной 3 мкм? Сколько зон Френеля возникает в данном случае?
237*. Определить показатель преломления тонкого прозрачного клина, освещаемого монохроматическим светом с длиной волны 0,48 мкм, падающим нормально на его поверхность, если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,32 мм, а угол клина = 5·10-4 рад.
238*. Тёмной или светлой будет в отраженном монохроматическом свете
мыльная
пленка (n
= 4/3) толщиной d
= 3![]() мкм
при нормальном падении лучей с длиной
волны 600 нм ?
мкм
при нормальном падении лучей с длиной
волны 600 нм ?
239*. Определить радиус кривизны линзы, если радиус 13 светлого кольца Ньютона, наблюдаемыми в отраженном свете с длиной волны 648 нм при нормальном её падении, равно 3,6 мм.
240*. Дифракционная решетка содержит N = 200 штрихов на каждый миллиметр ее длины. На решетку падает нормально свет с длиной волны λ= 0,56мкм. Под какими углами к оптической оси прибора могут наблюдаться два первых главных максимума? Найти наибольшее значение m порядка главных максимумов.
241*. Электрон находится в потенциальном ящике шириной 0,2 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
242.
Излучение возбужденного атома происходит
в течение времени ![]() ,
длина волны излучения
,
длина волны излучения ![]() .
Определить, с какой наибольшей точностью
.
Определить, с какой наибольшей точностью
![]() может быть найдена энергия E
излучения.
может быть найдена энергия E
излучения.
243.
Атом испустил фотон с длиной волны ![]() .
Продолжительность излучения
.
Продолжительность излучения ![]() .
Определить наибольшую точность
.
Определить наибольшую точность ![]() ,
с которой может быть измерена длина
волны излучения.
,
с которой может быть измерена длина
волны излучения.
244*. Сколько целых волн де Бройля уложится на длине пятой орбиты возбужденного электрона в атоме водорода?
245*. Энергия возбужденного электрона, находящегося в потенциальном квантовом ящике на четвертом энергетическом уровне, равна 0,86 эВ. С какой неопределенностью может быть установлена скорость электрона?
246.
Используя соотношение неопределенностей,
оценить наименьшие ошибки ![]() в определении скорости электрона и
протона, если координаты центра масс
этих частиц могут быть установлены с
неопределенностью
в определении скорости электрона и
протона, если координаты центра масс
этих частиц могут быть установлены с
неопределенностью ![]() .
.
247.
Протон находится в одномерном
потенциальном ящике. Используя
соотношение неопределенностей, оценить
ширину
ящика, если известно, что минимальная
энергия ![]() протона равна 20 МэВ.
протона равна 20 МэВ.
248.
Найти отношение длин волн де Бройля
электрона и протона, прошедших одинаковую
ускоряющую разность потенциалов ![]() .
.
249.
Пользуясь соотношением неопределенностей,
оцените размеры атома, если электрон
в нем движется со скоростью, отвечающей
прохождению ускоряющего потенциала
![]() .
.
250. Используя соотношение неопределенностей, оценить ширину одномерного потенциального ящика, в котором минимальная энергия электрона равна 1 эВ.
251*.Частица
находится в потенциальном ящике. Найти
соотношение разности соседних
энергетических уровней ![]() к энергии
к энергии ![]() частицы в случаях: 1) n=2,
2) n=10.
частицы в случаях: 1) n=2,
2) n=10.
252*.
Определить максимальную энергию
фотона серии Пашена в спектре излучения
атомарного водорода. Найти наибольшую
![]() и наименьшую
и наименьшую ![]() длины волн в спектре излучения.
длины волн в спектре излучения.
253*.
Частица в потенциальном ящике шириной
находится в возбужденном состоянии
![]() .
Определить, в каких точках интервала
.
Определить, в каких точках интервала
![]() плотность вероятности нахождения
частицы имеет максимальное и минимальное
значение.
плотность вероятности нахождения
частицы имеет максимальное и минимальное
значение.
254*.
Квант энергии ![]() выбивает электрон из атома водорода,
находящегося в третьем энергетическом
состоянии. Определить кинетическую
энергию (в электрон-вольтах) выбитого
электрона.
выбивает электрон из атома водорода,
находящегося в третьем энергетическом
состоянии. Определить кинетическую
энергию (в электрон-вольтах) выбитого
электрона.
255*. В однозарядном ионе гелия электрон перешел со второго энергетического уровня на первый. Определить длину волны излучения исходя и теории Бора.
256*. Из атома водорода, находящегося во втором энергетическом состоянии, в результате поглощения фотона вылетает электрон, кинетическая энергия которого вдали от ядра равна 10 эВ. Определить энергию фотона (в электрон-вольтах).
257*.
Исходя из полуклассической теории
атома Бора, определить первый потенциал
![]() возбуждения и энергию ионизации
иона
возбуждения и энергию ионизации
иона ![]() ,
находящегося в основном состоянии.
,
находящегося в основном состоянии.
258*.Электрон находится в потенциальном ящике шириной . В каких точках в интервале плотность вероятности нахождения электрона на первом и втором энергетическом уровнях одинакова? Вычислить значение плотности вероятности для этих точек. Решение пояснить графиком.
259*.
Электрон находится в потенциальном
ящике с бесконечно высокими стенками
(металл), размеры которого около 1 см.
Какую минимальную энергию нужно сообщить
электрону для перехода из основного
состояния на второй (возбужденный
электрон) энергетический уровень ![]() .
.
260*. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W обнаружить частицу в средней трети ящика?
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
по разделу «Колебания и волны»
