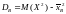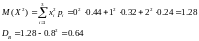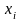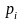БСТ19ХХ / Теорвер_7

Вариант 07

Задание 1

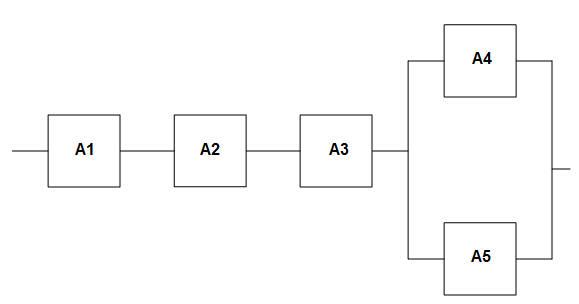
Электрическая цепь состоит из пяти элементов, выход из строя которых в заданный промежуток времени – независимые события, имеющие вероятности p_i = 0.1 каждый. Найти вероятность Р отказа цепи за данный промежуток времени.

Решение

Рассмотрим порядок соединения для получения приведенной электрической схемы.

1. Элементы 1, 2 и 3 соединены последовательно в участок 1-3.

2. Элементы 4 и 5 соединены параллельно в участок 4-5.

3. Участки 1-3 и 4-5 соединены последовательно.

Введем следующие обозначения событий:

A_i – работает элемент i (i=1, 2, …, 5),

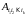– работает участок соединения из элементов .

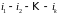По условию задачи

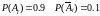
Необходимо найти вероятность события .

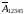Будем находить вероятности событий, перечисленных в порядке соединения схемы.

При этом будем помнить, что для параллельного соединения проще найти вероятность отказа участка (все элементы соединения не работают), а для последовательного соединения проще найти вероятность работы участка (все элементы соединения работают).

Для участка 1-3 находим вероятность работы.

Для участка 4-5 находим вероятность отказа.

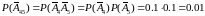
Вероятность работы цепи:

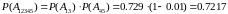
Мы нашли вероятность работы цепи. Вероятность отказа:

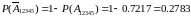
Ответ: 0.2783.

Задание 2

Дискретная случайная величина задана законом распределения p_i(x_i). Найти величину a, построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.

	1	3	5	7	9
	0,1	0,2	0,3		0,1

Решение

Так как сумма вероятностей должна быть равна 1, то величина а равна:

а = 1 – (0.1 + 0.2 + 0.3 + 0.1) = 0.3

Найдем функцию распределения:

Для нахождения интегральной функции распределения пользуемся ее определением применительно к каждому из промежутков изменения с.в.

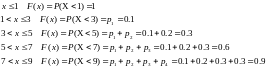
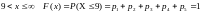
Вид функции распределения:

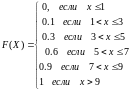
График функции распределения:

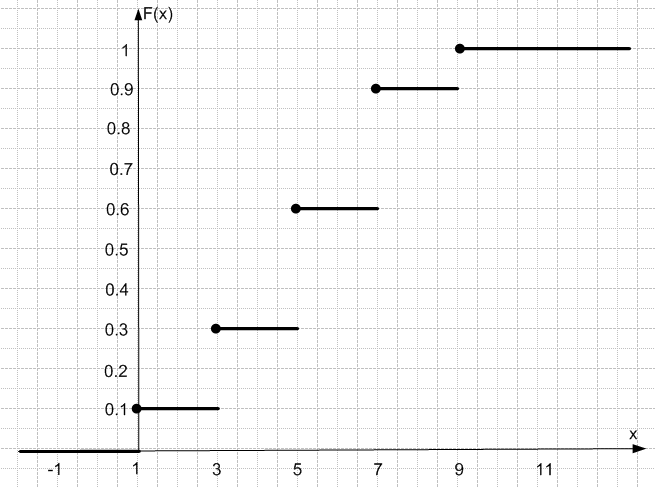
Математическое ожидание:

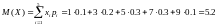
Найдем дисперсию:

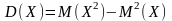
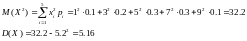
Среднее квадратическое отклонение:

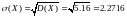
Задание 3

Функция распределения непрерывной случайной величины задана выражением:

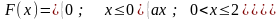
Найти величину коэффициента а, написать аналитическое выражение и простроить графи плотности распределения вероятностей, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (0; 1) и (1; 4).

Решение

Так как в конечной точке должно выполняться равенство F(2) = 1, то:

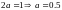
Плотность распределения равна первой производной от функции распределения. Поэтому:

Найдем математическое ожидание:

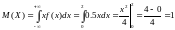
Чтобы найти дисперсию непрерывной случайной величины Х, найдём математическое ожидание случайной величины Х :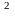

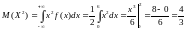
Дисперсию найдем по формуле:

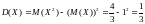
Среднее квадратическое отклонение:

График плотности распределения:

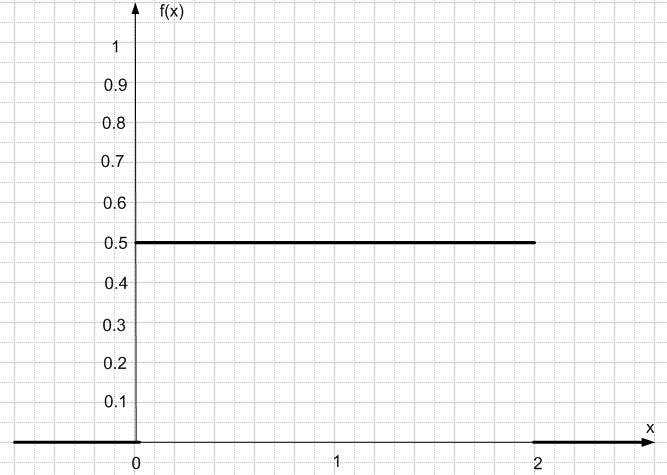
Вероятность попадания непрерывной случайной величины в интервал найдем по формуле:

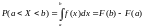
Поэтому:

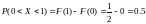
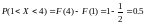
Задание 4

Дана нормально распределенная случайная величина с математическим ожиданием m = 2 и дисперсией σ² = 3. Найти вероятность попадания данной случайной величины в интервал (0; 4).

Решение

Для нормального распределения вероятность попадания случайной величины в интервал определяется по формуле:

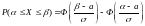
где Ф(Х) – функция Лапласа, значения которой определяются по таблицам,

В данном случае:

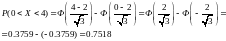
Ответ:

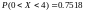
Задание 5

Дискретная случайная величина задана выборкой:

0, 1, 2, 1, 0, 2, 0, 1, 2, 0, 0, 0, 1, 1, 1,2, 0, 1, 0, 0, 2, 1, 2, 0, 0

Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию.

Решение

Составим ряд распределения в виде таблицы:

xi	0	1	2
ni	11	8	6

Строим полигон частот:

Находим относительные частоты:

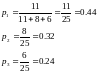
Тогда функция распределения:

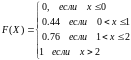
График функции распределения:

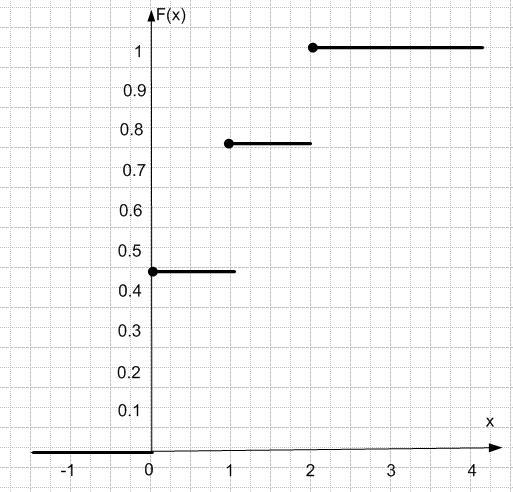
Выборочное среднее:

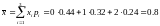
Найдем выборочную дисперсию: