
БСТ19ХХ / Вариант №7
.docxДесятилетие Г исключается (просто откидывается). В результате получаем ДДММг. Полученное число нужно перевести в двоичный формат представления данных. Результат необходимо дополнить до 16 разрядов дописав перед числом необходимое количество нулей.
Тогда 23.05.2001 = 23.05.01 = 23051 = 101101000001011.
Дополняем до 16-ти разрядов нулями в старших разрядах: 1011010000010110 – результирующая логическая функция.
х3 |
х2 |
х1 |
х0 |
f |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Таблица 1. Сформированный вариант задания
Задание
1. Реализовать полученную функцию на логических элементах
Задание 1.
В результирующей логической функции количество единиц меньше, чем нулей. Поэтому рационально использовать совершенную дизъюнктивную нормальную форму (СДНФ).
f(х3, х2, х1, х0) = ͞х3͞х2͞х1͞х0 + ͞х3͞х2х1͞х0 + ͞х3͞х2х1х0 + ͞х3х2͞х1х0 + х3͞х2х1х0 + х3х2͞х1х0 + х3х2х1͞х0.
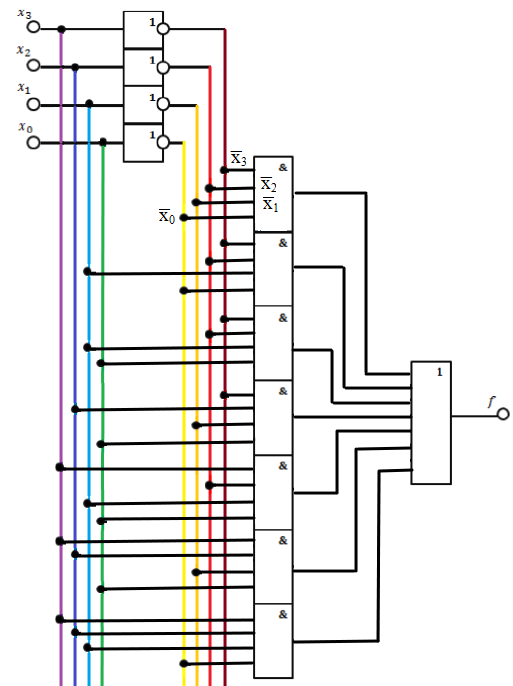
Рис. 1. Схема реализации функции на логических элементах
3. Выполнить минимизацию по карте Карно, синтезировать схему на базисе, определенном вариантом, привести синтезируемую схему, выполнить проверку на соответствие исходной таблице истинности.
5-8 вариант → ИЛИ-НЕ
Минимизация по карте Карно:
х1 х0
|
|
01 |
|
|
00 |
1 |
0 |
|
1 |
01 |
0 |
|
0 |
0 |
11 |
0 |
|
0 |
1 |
10 |
0 |
0 |
|
0 |
fМДНФ = ͞х3͞х2͞х0 + х2͞х1х0 + ͞х2х1х0 + х3х2х1͞х0.
Таблица истинности МДНФ:
х3 |
х2 |
х1 |
х0 |
͞х3 |
͞х2 |
͞х1 |
͞х0 |
͞х3͞х2͞х0 |
х2͞х1х0 |
͞х2х1х0 |
х3х2х1͞х0 |
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблица истинности минимизированной функции совпадает с таблицей истинности исходной функции.
 Для
того чтобы реализовать логическую
функцию, заданную в ДНФ, в базисе ИЛИ-НЕ,
необходимо взять двойное отрицание от
этой функции и по законам де Моргана
заменить все конъюнкции на дизъюнкции,
т.е.:
Для
того чтобы реализовать логическую
функцию, заданную в ДНФ, в базисе ИЛИ-НЕ,
необходимо взять двойное отрицание от
этой функции и по законам де Моргана
заменить все конъюнкции на дизъюнкции,
т.е.:
͞х3͞х2͞х0 + х2͞х1х0 + ͞х2х1х0 + х3х2х1͞х0 =
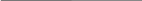


 =
͞х3͞х2͞х0
∙ х2͞х1х0
∙ ͞х2х1х0
∙ х3х2х1͞х0
=
=
͞х3͞х2͞х0
∙ х2͞х1х0
∙ ͞х2х1х0
∙ х3х2х1͞х0
=

= (х3 + х2 + х0)∙(͞х2 + х1 + ͞х0)∙(х2 + ͞х1 + ͞х0)∙(͞х3 + ͞х2 + ͞х1 + х0) =

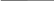
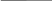
 =
х3
+ х2
+ х0
+ ͞х2
+ х1
+ ͞х0
+ х2
+ ͞х1
+ ͞х0
+ ͞х3
+ ͞х2
+ ͞х1
+ х0.
=
х3
+ х2
+ х0
+ ͞х2
+ х1
+ ͞х0
+ х2
+ ͞х1
+ ͞х0
+ ͞х3
+ ͞х2
+ ͞х1
+ х0.
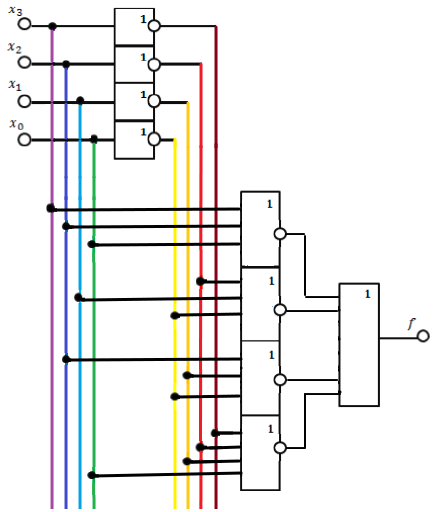
Рис. 2. Минимизированная логическая схема в базисе «ИЛИ-НЕ»
х3 |
х2 |
х1 |
х0 |
͞х3 |
͞х2 |
͞х1 |
͞х0 |
|
͞х2 + х1 + ͞х0 |
|
|
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |

 х3
х2
х3
х2 00
00 11
11 10
10 1
1 1
1 1
1 1
1 х3
+ х2
+ х0
х3
+ х2
+ х0 х2
+ ͞х1
+ ͞х0
х2
+ ͞х1
+ ͞х0 ͞х3
+ ͞х2
+ ͞х1
+ х0
͞х3
+ ͞х2
+ ͞х1
+ х0