Лекции / СТКУ_какие_то_лекции

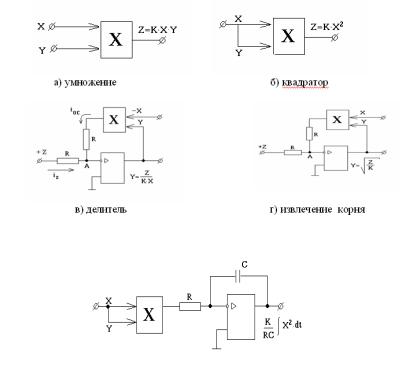
Схема устройства вычисления среднеквадратичного значения (рис.11-1 д) содержит умножитель и интегратор на основе ОУ.

д) вычисление среднеквадратичного значения

рис.11-1

Помимо указанных операций умножитель может осуществлять преобразование частоты, может быть использован в качестве модулятора, преобразователя частоты, фазового детектора и т.д..

11.1.3. Умножитель с переменной крутизной (общий принцип)

Статическая крутизна транзистора:

S Ik Ik

Uбэ T ,

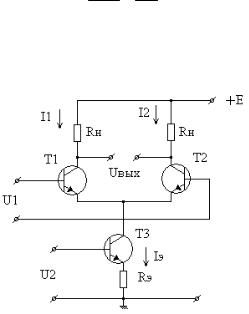
где T – температурный потенциал. Рассмотрим ДК (рис.11-2):

рис.11-2

Для значений

U1 T

Крутизну S можно изменять при помощи U2.

Тогда крутизна S для транзистора Т1 (или Т2) определяется при симметрии ДК:

а выходное напряжение ДК:

Uвых S U1 Rн U1 U2 Rн ,

2 Т Rэ

то есть Uвых пропорционально произведению U1 и U2.

11.2. Повторитель напряжения

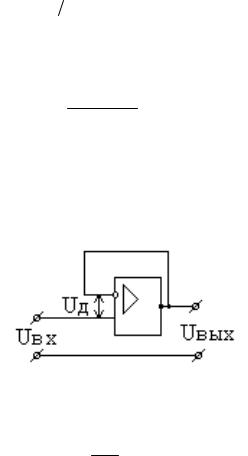
Для схемы рис.11-3

рис.11-3

UД Uвых 0,

KU

так как КU стремится к бесконечности.

И так как UД = 0, то Uвх Uвых .

В схеме ООС – последовательная, по напряжению (100%); сигнал подается на неинвертирующий вход.

Схема называется «повторитель напряжения», так как

Uвх Uвых и по амплитуде и по фазе. Для этой схемы характерный признак:

11.3. Активные фильтры на основе операционных усилителей

В современной радиоэлектронике все большее применение находят активные RC – фильтры (ARC). Их практическая ценность – отсутствие катушек индуктивностей, что позволяет их применять на очень низких частотах; они могут быть изготовлены методами интегральной микроэлектронной технологии.

Название ARCфильтры (активные RC-фильтры) связано с тем, что в них применяются активные ОУ и пассивные

RC – цепи.

Преимущества ARC – фильтров

1.Отсутствие катушек индуктивностей L – элементов (которые нуждаются в экранировании; LRC фильтры имеют большие габариты, массу и стоимость, нетехнологичны);

2.Дешевы, малогабаритны и технологичны;

3.Параметры RC –фильтров ближе к идеальным;

4.ARC –фильтры дают усиление в полосе пропускания;

5.Использование ОУ дает развязку RВЫХ от RВХ;

6.Легче настраивать;

7.Более надежны, чем LC – фильтры. Недостатки ARC – фильтров.

1.Нуждаются в источниках питания;

2.Рабочий диапазон ограничен максималной частотой

fmax ОУ (несколько Мгц);

3.Параметры элементов ARC – фильтров должны иметь малый разброс и малые температурные коэффициенты, малые временные дрейфы параметров. Для схем фильтров второго порядка допуск должен составлять для конденсаторов С ±5% и для резисторов R ±2%. Для схем более высоких порядков должен быть еще меньший допуск.

4.В схемах ARC – фильтров должны быть малошумящие элементы. Из конденсаторов лучше всего применять полистироловые, керамические, слюдяные. Дисковые керамические конденсаторы имеют малое применение, так как у них плохая стабильность по температуре, времени и частоте.

11.3.1. Активные RC – фильтры нижних частот первого порядка. Обобщенное описание фильтра НЧ

Исходная формула коэффициента передачи:

1 .

1 j RC

Введем комплексную нормированную переменную

p=j + ,

где - допустимое отклонение АЧХ в полосе пропускания (обычно 2 1).

Введем обозначение р (нормированное значение час-

ср

тоты в операторной форме). Тогда при = 0 обозначим:

Pp R C

икоэффициент передачи в операторной форме

K P 1 1 P

для фильтра первого порядка.

При 1, т.е. f fcp, |K| = 1/ , что соответствует снижению К на 20дБ на декаду (изменению в 10 раз). Для более крутого изменения затухания включают последовательно несколько фильтров. Тогда, в общем случае, коэффициент передачи (передаточная функция) ФНЧ в операторной форме может быть записана:

где:

К0 – коэффициент передачи фильтра при Р = 0;

ai, bi – положительные действительные коэффициенты; i = 1..n/2 для четных n;

i = 2..(n+1)/2 для нечетных n;

n – порядок фильтра определяемый степенью Р после перемножения в знаменателе. Порядок фильтра определяет наклон АЧХ после частоты среза fcp.. Вид характеристики определяется как порядком, так и типом фильтра (Чебышев, Баттерворт и др.)

Типы фильтров отличаются значениями ai, bi в передаточной функции. Их значения можно найти в литературе (например, У.Титце, К.Шенк 1982г., стр. 194-198)

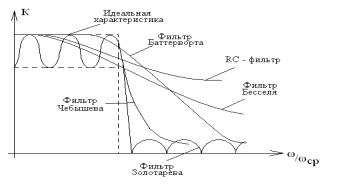
Пример: фильтры шестого порядка имеют следующие примерные характеристики (рис.11-4):

рис.11-4

Создание фильтра начинают с выбора его АЧХ и требований к ней (полоса пропускания; частота среза fсреза; скорость спада АЧХ; коэффициент затухания; неравномерность в полосе и иногда за ее пределами). Нужно знать порядок фильтра (число полюсов функции). Обычно число полюсов показывает на скорость спада функции – АЧХ фильтра. Обычно скорость равна n·20 дБ/декаду. На каждый полюс фильтра обычно приходится один конденсатор фильтра. Число конденсаторов равно порядку фильтра.

Фильтр Баттерворта: АЧХ с максимально плоской характеристикой в полосе, но небольшая скорость спада затуха-

ния, что принимают, когда высоки требования к равномерности в полосе пропускания.

Фильтр Чебышева: имеет неравномерность в полосе пропускания, но хороший спад АЧХ за полосой; неравномерность в полосе нужно задавать.

Фильтр Бесселя: АЧХ неважная. Но фильтр максимально без искажений передает форму сигналов, так как у него очень хорошая фазовая характеристика (линейная ФЧХ), что особенно важно для прямоугольных импульсов.

Фильтр Золотарева: имеет максимальный спад за полосой пропускания, но имеет неравномерность как в пределах полосы, так и за полосой пропускания, что нужно регламентировать.

11.3.2. Реализация ARC – фильтра нижних частот первого порядка

Передаточная функция имеет вид:

(P) 0

1 a1P

где а1 = 1, К0 = 1+R2/R3, fcp = 1/2 R1C1.

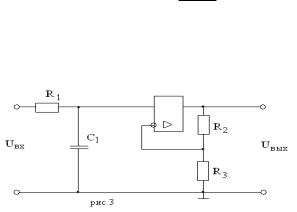
Его реализация (рис.11-5):

рис.11-5

11.3.4. Реализация ФВЧ на ARC

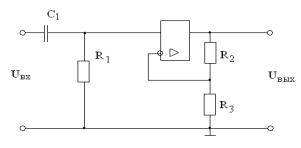
Нужно заменить P на 1/Р, а в схеме рис.11-5 поменять R1 и C1 местами (рис.11-6).

K = 1+R2/R3; ai = 1; bi = 0.

рис.11-6

11.3.5. Реализация ARC – фильтров НЧ и ВЧ второго порядка

Передаточная функция ФНЧ второго порядка может быть записана в общем виде:

Такие функции характеризуются (второго и более порядков) наличием комплексно-сопряженных полюсов. Такие функции не могут быть реализованы с помощью пассивных элементов RC. Один из способов их реализации - применение индуктивностей (L элементов) . Другой способ – применение RC – цепей с ОУ.

Реализация ARC – фильтров НЧ и ВЧ обычно выполняется на основе ОУ:

- либо со сложной ООС; - либо с ПОС (фильтры Саллена – Кея). Обратная связь используется для формирования комплексно-сопряженных полюсов.

11.3.6. Фильтр НЧ со сложной ООС

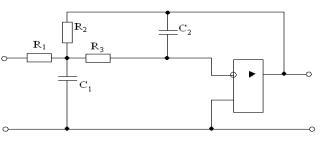
Фильтр со сложной ООС (многопетлевой ООС) носит название фильтра со структурой Рауха (рис.11-7). Для ФНЧ Баттерворта а1 = 1,44, b1 = 1.

Для него:

рис.11-7