Демин / экзамен / готовые решения / 9 (без 6)
.pdf
1. Известно, что P(A) + 0,5 P(B) 1.1, 0,5 P(A) + 1,5 P(B) 1,7. Верно ли утверждение, что события A и B образуют полную группу событий?
(2) – 3(1): -2,5 P(A) = -1,6 => P(A) = |
16 |
|||||||||||||
25 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
P(B) = |
11 |
– |
16 |
|
|
|
|
|
|
|
|
||
2 |
10 |
25 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
1 |
P(B) = |
55−32 |
=> P(B) = |
23 |
* |
2 |
= |
23 |
|
|
||||
2 |
|
50 |
|
25 |
|
|
||||||||
|
50 |
|
|
|
1 |
|
|
|
||||||
Теорема: сумма вероятностей A1, …, An, образующих полную группу, равна 1. P(A) + P(B) = 1625 + 2325 != 1 => события A и B не образуют полную группу событий.
2. На плоскости даны две концентрические окружности, радиусы которых равны 1 см и 2 см. Найти вероятность того, что точка, брошенная наудачу в больший круг, попадёт в меньший круг.
P(A) = |
(1) |
= |
|
= |
1 |
|
(2) |
4 |
4 |
||||
|
|
|
3. Локальная теорема Муавра-Лапласа
Если в n независимых испытаний, в каждом из которых есть событие, которое может произойти с одной и той же вероятностью p. Тогда при больших n вероятности можно вычислять по приближенным формулам Муавра-Лапласа:
4. По каналу связи передано n = 100 символов. Искажение одного символа происходит с вероятностью p = 0,05. Найти вероятность того, что будет искажено менее двух символов.
λ = np = 100 * 0,05 = 5 => 100( ) = 5 −5
!
50 51100( < 2) = 0! −5 + 1! −5
5. Пусть случайная величина X – число вызовов, поступающих на АТС за 5 сек, распределена по закону Пуассона с параметром 12 вызовов за 3 сек. Найти дисперсию случайной величины X.
P(X = k) = λ ! −λ, где λ = 12
t = 53 => λ1 = t * λ = 53 * 12 = 20 = D[X] (тк мат ожидание и дисперсия случайной величины Х в распределении Пуассона: M[X] = D[X] = )
6.Случайная величина подчиняется равномерному закону распределения. Найти математическое ожидание случайной величины Y = 2+1.
7.Укажите формулу вычисления коэффициента корреляции двух непрерывных случайных величин.
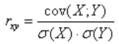но мат ожидания и дисперсия вычисляются с помощью интегралов:
8. Задана плотность распределения p (x) X случайной величины X:
Найти вероятность события A | X mX |1/ 4. Оценить эту вероятность по неравенству Чебышева.
9. Выборка для некоторой изучаемой случайной величины содержит 15 значений и имеет вид: –1, 0, 0, 1, 1, 0, –1, 1, 0, 0, 1, –1, –1, 1, 1. Найти выборочное среднее, медиану и моду данной выборки.
Запишем выборку в виде вариационного ряда: -1, -1, -1, -1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1 Запишем статистическое распределение выборки в виде дискретного
статистического распределения частот:
xi |
-1 |
0 |
1 |
̅= |
−1 4+0 5+1 6 |
= |
2 |
|
Me(X) = |
|
– тк n – нечетное => Mo(X) = x8 = 0 |
|
|
|
|
|
|
||||||||
ni |
4 |
5 |
6 |
15 |
|
15 |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mo(X) = 1 (варианта, встречающаяся чаще всего в вариационном ряду)
10. Сформулируйте критерий проверки параметрической гипотезы Н0 : 2 = 02 против альтернативы Н0 : 2 != 02 на уровне значимости для выборки объема n, полученной из нормально распределенной генеральной совокупности с известным математическим ожиданием
Для проверки нулевой гипотезы вычисляется наблюдаемое значение критерия
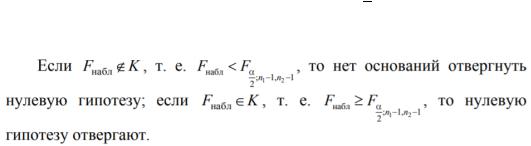
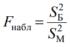. Критическая область имеет вид: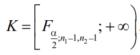 
Где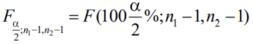 
- 1002 – процентная точка распределения
Фишера с (n1 - 1) и (n2 - 1) степенями свободы; n1, n2 – объемы выборок с большей и меньшей дисперсиями.