
11 вариант
1. Запишите теоремы сложения и умножения вероятностей для двух событий.
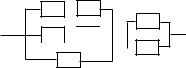
2. Даны вероятности pi безотказной работы в течение гарантийного срока отдельных элементов
цепи, представленной на рисунке ниже. Отказы отдельных элементов цепи независимы. Определить вероятность работы цепи в течение этого срока.
1 |
|
2 |
|
6
3 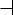 4
4 



 7
7
5
3.12 деталей, среди которых 3 шестеренки, 5 конденсаторов и 4 шарика распределяются случайным образом в три ящика так, чтобы в каждый ящик попало бы одинаковое число деталей. Какова вероятность того, что в каждом ящике находится по одной шестеренке?
4.Напишите формулу Пуассона и укажите смысл входящих в нее параметров.
5. Случайные величины X и Y независимы и распределены: X по закону R( 1, 5) , Y – по закону с плотностью pY ( y) 2 2 y , y [0, 1] . Вычислить M ( XY 2X 3Y ) .
6.Случайная величина X получена в результате суммирования 300 независимых случайных величин, распределенных по одному и тому же равномерному закону на отрезке [0, 0.4]. Найдите дисперсию случайной величины X .
7.По результатам наблюдений, сведенным в таблицу
|
xi |
1 |
2 |
5 |
8 |
|
|
|
|
|
ni |
10 |
25 |
10 |
5 |
|
|
|
|
найдите несмещенную оценку |
S 2 для дисперсии 2 . Здесь n |
- число наблюдений, равных |
x |
. |
|||||
|
|
|
|
|
|
i |
|
i |
|
|
|
~ |
|
||
8. |
Сформулируйте свойство эффективности оценки n неизвестного параметра . |
|
|||
9. |
По выборке объема n 17 из нормального распределения N (m, 2 ) получены значения S 2 |
4 , |
|||
|
|
|
|
2,2. Найти доверительный интервал для дисперсии генеральной совокупности с |
|
|
|
X |
|
||
|
доверительной вероятностью 0,95. ( 162 ;0.975 28.8) |
|
|||
10. |
|
|
Напишите формулу вычисления статистики критерия 2 Пирсона. |
|
|

12 вариант
1.Упростить A B A B A B AB
2.Из урны, содержащей 10 белых и 8 черных шаров наудачу отобрали 3 шара. Рассматриваются события: A ={появится один черный шар}, B ={появится хотя бы один белый шар}. Найти вероятность P( A | B) .
3.Написать формулу Бернулли и пояснить смысл входящих в нее параметров.
4.Две радиостанции передают сигналы, 1-ая вдвое чаще, чем 2-ая. Вероятности приёма их сигналов соответственно равны 0,6 и 0,8. Известно, что сигнал принят. Какова вероятность того, что он передан станцией №1.
5.Напишите формулу вычисления математического ожидания случайной величины X , если известна совместная плотность распределения p XY (x, y) случайного вектора ( X ,Y ) .
6.Случайные величины X и Y независимы и распределены: X по закону R(0,6) , Y – по
показательному закону с параметром 1/ 3 . Вычислить D(2 X Y ) ,
7.По результатам наблюдений, сведенным в таблицу
|
xi |
1 |
3 |
5 |
|
7 |
|
|
ni |
10 |
25 |
10 |
|
5 |
|
найдите выборочное среднее. Здесь ni |
- число наблюдений, равных xi . |
||||||
8.Сформулируйте метод моментов получения точечных оценок.
9.По выборке объема n 25 со средним значением x 9.5 , полученной из нормального
распределения с известной дисперсией 2 1, на уровне значимости 0.05 проверить гипотезу H0 :m 10 при альтернативе H1 :m 10 . (U0.975 1.96 )
10.Сколько степеней свободы нужно взять для квантили распределения 2 при проверке
гипотезы по критерию Пирсона о том, что выборка, сгруппированная на 6 интервалов, была получена из гипотетического распределения с двумя неизвестными параметрами?
13вариант
1.Из цифр 1, 2, 3, 4, 5, 6 наудачу с возвращением составляется пятизначное число. Найти вероятность P( A | B) , если события A = {число будет нечетным}, B = {цифры 1 и 2 не появились}.
2.В урне содержится 4 белых, 3 красных и 3 черных шара. Производится извлечение пяти шаров без возвращения. Найти вероятность того, что в результате извлечений появилось 3 белых шара
ипо одному остальных цветов.
3.По каналу связи передается 2000 знаков, каждый из которых, независимо от других, может быть искажен с вероятностью 0,001. Найти вероятность того, что будет искажено не более двух знаков.
4.Укажите основные свойства математического ожидания случайной величины.
5. Случайные величины X и Y независимы и известны их одномерные законы распределения:
|
X : |
0 |
1 |
2 |
3 |
|
Y : |
–1 |
0 |
1 |
|
0,2 |
0,5 |
0,1 |
0,2 |
|
0,3 |
0,5 |
0,2 |
||
|
|
|
|
|||||||
Найти вероятность события X Y 2 . |
|
|
|
|
||||||
6. Случайные величины X и Y имеют совместную плотность распределения
с(x y), если 0 x 2, 0 y 2; pXY (x, y)
Найти константу c и математическое ожидание случайной величины Z XY .
7.Складываются 200 независимых и одинаково распределенных случайных величин по показательному закону с параметром 5. Используя предельную теорему, найти плотность распределения этой суммы.
8.По результатам наблюдений, сведенным в таблицу
xi |
1 |
3 |
8 |
ni |
10 |
4 |
1 |
найдите выборочную дисперсию. Здесь ni - число наблюдений, равных xi .
9.Найти оценку методом моментов параметра по выборке объема n , полученной из биномиального распределения Bi(1, ) , используя 2-й начальный момент.
~
10. Какими свойствами обладает оценка n неизвестного параметра , полученная методом максимального правдоподобия?

14вариант
1.Найти случайное событие X из равенства: X A X A .
2.Даны вероятности pi безотказной работы в течение гарантийного срока отдельных элементов цепи, представленной на рисунке ниже. Отказы отдельных элементов цепи независимы. Определить вероятность работы цепи в течение этого срока.
1
2 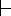
 3
3
4
5 
 6
6 
 7
7
3.В группе из 25 студентов 20 человек изучают английский язык, 10 – изучают немецкий и 7 – изучают оба языка. Найти вероятность того, что выбранный наудачу студент изучает только один из языков.
4.Напишите общую формулу вычисления коэффициента асимметрии случайной величины.
5.Укажите основные свойства ковариации двух случайных величин.
6.Случайный вектор ( X ,Y ) распределен равномерно внутри области
G (x, y) : x y 2, x 0, y 0 . Найти математическое ожидание случайной величины
Z XY .
7.Случайная величина X имеет характеристики: mX 2 , X 1/ 2 . Оценить сверху по неравенству Чебышева вероятность события X 3.
8.Вычислить выборочное среднее для выборки: 5, 2, 4, 3, 2, 2, 3, 2, 1, 5, 3, 4, 5, 3, 3, 2, 1, 1, 2, 4.
9.Чему равны математическое ожидание и дисперсия выборочного среднего для выборки объема n , полученной из нормального распределения с параметрами: m 1, 0.5 ?
10.По выборке объема n 16 , полученной из нормального распределения N (m, 4) , было
найдено X 2,2. Построить доверительный интервал для параметра m с доверительной вероятностью 0,95. (U0.975 1.96 )
15вариант
1.Бросают две игральных кости. Событие A - выпадение единицы на первой кости, событие B - выпадение двойки на второй кости. Вычислить вероятность P( A B) .
2.Прибор состоит из трех последовательно включенных узлов. Вероятности отказа первого, второго и третьего узлов равны 0.2, 0.3 и 0.1. Найти вероятность того, что за время испытаний откажет ровно один узел прибора.
3.Полиномиальная схема.
4.Система запрашивает передачу некоторого сигнала три раза подряд. Вероятность правильного приема системой этого сигнала при первой, второй и третьей передачи соответственно равны 0.9, 0.7, и 0.5. Найти вероятность того, что система правильно примет сигнал два раза.
5.Случайная величина X распределена по непрерывному закону с плотностью распределения
p X (x) x / 2, 0 x 2 . Найти квантиль случайной величины X на уровне p 1/ 2 .
6.Напишите формулу вычисления ковариации для дискретных случайных величин.
7.Случайный вектор ( X ,Y ) распределен равномерно внутри квадрата {0 x 2, 0 y 2}. Найти математическое ожидание M ( X Y ) .
8.По данному статистическом ряду
xi |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
ni |
3 |
2 |
2 |
3 |
1 |
2 |
1 |
найдите выборочную медиану. Здесь ni - число наблюдений, равных xi .
~
9. Дайте определение состоятельности оценки n параметра .
10. При 180 бросаниях игральной кости шестерка выпала 36 раз. По критерию Пирсона проверить согласие этого результата с утверждением, что кость правильная? Принять уровень
значимости 0, 05 ( 02,95;1 3.84 ).

16вариант
1.Укажите основные свойства операций над событиями.
2.Игральная кость подбрасывается один раз. Рассматриваются три события: A - выпадет четное число очков, B - число очков кратно пяти, С - число очков больше трех. Будут ли эти три события независимыми попарно и в совокупности? Результат обосновать.
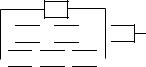
3.Даны вероятности pi безотказной работы в течение гарантийного срока отдельных элементов цепи, представленной на рисунке ниже. Отказы отдельных элементов цепи независимы. Определить вероятность работы цепи в течение этого срока.
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
||
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
7 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Обобщенная схема независимых испытаний Бернулли с различными вероятностями появления события в одном испытании.
5.Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при четырехкратной передаче сигнал будет принят ровно 1 раз.
6.Случайная величина X распределена по закону, определяемому таблицей
xi |
–2 |
0 |
2 |
|
|
|
|
pi |
3/5 |
1/5 |
1/5 |
|
|
|
|
Найти коэффициент корреляции между случайными величинами X и X 2 .
7.Сформулировать теорему Бернулли как следствие из закона больших чисел.
8. Вычислить выборочную квантиль на уровне p 1/ 4 для выборки: 2, 3, 1, 1, 1, 2, 3, 2, 1, 5, 3, 4,
5, 3, 3, 2, 1, 1, 2, 5.
9.Напишите формулу вычисления доверительного интервала для параметра 2 с доверительной
вероятностью для выборки объема n , полученной из нормального распределения N(m, 2 ) , при известной величине m .
10. Сформулировать метод максимального правдоподобия для поиска точечной оценки ~ по
n
выборке объема n , полученной из дискретного распределения, зависящего от одного параметра .
17вариант
1.Определение условной вероятности событий A и B . Условие их независимости.
2.Из колоды в 36 карт наудачу и последовательно извлекли 3 карты без возвращения. Найти
вероятность P( A | B) , где A ={будет хотя бы один туз}, B {все карты бубны}.
3. Даны вероятности pi безотказной работы в течение гарантийного срока отдельных элементов
цепи, представленной на рисунке ниже. Отказы отдельных элементов цепи независимы. Определить вероятность работы цепи в течение этого срока.
1
 2
2  3
3 
 7
7  4
4  5
5  6
6 
4.По каналу связи передаются два символа: нуль и единица. При передаче единица переходит в единицу с вероятностью 0.9, а нуль переходит в нуль с вероятностью 0.8. Найти вероятность того, что при передаче кодовой комбинации «1001» будет одна ошибка.
5.Напишите общую формулу вычисления коэффициента эксцесса случайной величины.
6.Плотность вероятности f X (x) задана выражением:
f(x) 4x3 ,0 x 1
Х0, x 0x 1.
Найти математическое ожидание случайной величины 2X 1.
7.По данной таблице построить гистограмму, полигон относительных частот и вычислить выборочное среднее значение
|
|
|
|
|
|
(xi 1 , xi ) |
(- ;7) |
(7; 9) |
(9; 11) |
(11; 13) |
(13;+ ) |
ni |
5 |
10 |
60 |
20 |
5 |
8.Найти оценку методом моментов параметра по выборке объема n , полученной из равномерного распределения R(0, ) , используя теоретическую дисперсию.
9. Пусть 1 , 2 ,..., n – независимые случайные величины с распределением N (0,1) . Какое
n
распределение имеет случайная величина k2 ?
k 1
10. При 100 бросаниях монеты "герб" появился 40 раз. Проверить по критерию Пирсона гипотезу о том, что монета была симметричной. Принять 0, 05 . ( 0,95;12 3.84 )
18вариант
1.Укажите комбинаторные формулы, используемые при поиске вероятности в схеме выбора без возвращения.
2.Статистика, собранная среди студентов одного из вузов, обнаружила следующие факты: 50% студентов учатся на 4 и 5, 20% занимаются спортом и только 5% студентов учатся на 4 и 5 и занимаются спортом. Найти вероятность того, что студент занимается только одним видом деятельности.
3.По каналу связи передают два вида сигналов: нуль и единица. В силу наличия помех нуль может быть искажен в единицу с вероятностью 0.1, а единица в нуль – с вероятностью 0.2. Найти вероятность того, что при передаче сообщения 101 будет ровно одна ошибка.
4.Случайная величина X распределена по непрерывному закону с плотностью распределения
p X (x) 2x, 0 x 1. Найти квантиль уровня p 1/ 4 этой случайной величины.
5.Напишите формулу вычисления дисперсии случайной величины X , если известна совместная плотность распределения p XY (x, y) случайного вектора ( X ,Y ) .
6.Случайная величина X распределена равномерно на интервале [–2; 2]. Используя неравенство Чебышева, оцените вероятность события A | X | 1 .
7.Чему равны математическое ожидание и дисперсия случайной величины, имеющей распределение хи-квадрат с числом степеней свободы, равным 3?
8.Дана выборка наблюдений некоторой случайной величины X :
0, 1, 5, 1, 6, 4, 2, 1, 2, 6, 2, 4, 2, 5, 6, 2, 1, 2, 4, 5.
Построить статистический ряд, полигон относительных частот и найти выборочные характеристики: моду и медиану.
~
9. Сформулируйте метод максимального правдоподобия получения точечной оценки n
параметра по выборке объема n , полученной из непрерывного распределения с плотностью вероятностей pX (x, ) .
10. По выборке объема n 64 , полученной из нормального распределения с неизвестной дисперсией, на уровне значимости 0.05 проверить гипотезу H 0 :m 10 при альтернативе
H1 :m 10 , если выборочное среднее x 10.2 . Квантиль распределения Стьюдента
t24; 0.975 2.064 .

19вариант
1.Дайте определение несовместности и независимости двух событий. Можно ли считать, что эти понятия пересекаются.
2.Из букв О,О,О,М,Л,К разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово “молоко”.
3.Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что третье орудие попало, если вероятности попадания в цель 1-м, 2-м и 3-м орудиями соответственно равны 0,7; 0,8; 0,9.
4.Стрелок стреляет по мишени до первого попадания. Вероятность попадания при каждом выстреле равна 0,3. Случайная величина X характеризует число произведенных выстрелов. Найдите математическое ожидание случайной величины X .
5.Укажите основные свойства дисперсии случайной величины X .
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
||
6. |
Задана функция распределения F ( x) |
|
|
, |
0 x 2 |
|
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
x 2. |
|
|||||
|
|
|
|
|
|
|
|
|
1, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Найти математическое ожидание случайной величины 2 . |
|
|||||||||||||||
7. |
Сформулировать теорему Пуассона как следствие из закона больших чисел. |
||||||||||||||||
8. |
По данному группированному статистическому ряду найти выборочное среднее: |
||||||||||||||||
|
|
|
(xi 1 ; xi ) |
|
(- ; 5) |
|
(5; 7) |
|
(7; 9) |
|
|
(9; |
11) |
|
(11; ) |
|
|
|
|
|
ni |
|
10 |
|
20 |
|
120 |
|
|
40 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ) , где - математическое |
|||||||
9. |
Пусть (x1,..., xn ) |
– выборка из нормального распределения N( , |
|||||||||||||||
|
ожидание, а 2 |
– дисперсия. Найти оценку параметра методом моментов, используя второй |
|||||||||||||||
|
начальный момент. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. |
По выборке |
объема |
n 16 |
из нормального |
распределения |
N (m,1) получено значение |
|||||||||||
X 2,2. Найти доверительный интервал для дисперсии генеральной совокупности с доверительной вероятностью 0,95. ( 162 ;0.975 28.8)

20вариант
1.Дать статистическое определение вероятности события.
2.Брошены две игральные кости. Найти вероятность P( A | B) , если события A {все выпавшие числа четные}, B {выпала одна шестерка}.
3.Прибор состоит из трех узлов, вероятности отказа которых равны: 0.1, 0.15 и 0.2. Для работы прибора достаточно, чтобы работал только один из его узлов. За время испытаний прибора был зафиксирован его отказ. Найти вероятность того, что при этом отказали только 1-й и 3-й узлы.
4.Случайная величина X распределена равномерно на интервале [ 1, 1]. Определите, чему равна квантиль уровня 0.9 этой случайной величины.
5.Напишите функцию распределения показательного закона с параметром 4 .
6.Найти вероятность попадания равномерно распределенной случайной величины X на отрезке [1,7] на множество | X mX | 1.
7. Дана ковариационная матрица |
|
1 |
3 |
|
двух случайных величин |
X |
и Y . Найти дисперсию |
K |
|
|
|
||||
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
случайной величины Z 4X Y .
8. По данной таблице построить гистограмму частот, найти выборочное среднее и выборочную
медиану. |
|
|
|
|
|
|
|
|
(xi 1 ; xi ) |
( ;1] |
(1, 3] |
(3, 5] |
(5, 7] |
(7; 9] |
(9; ) |
|
ni |
10 |
25 |
20 |
30 |
10 |
5 |
( ni – число наблюдений, попавших в интервал (xi 1 , xi ) ).
9.Напишите формулу несмещенной оценки дисперсии для выборки объема n .
10.По результатам 100 измерений диаметра покрышки прибором, не имеющим систематических ошибок, было получено X 10.2. Найти 95%-ный доверительный интервал для математического ожидания (считать, что выборка получена из нормальной совокупности с
известной дисперсией 2 4 ). (U0.975 1.96 )
