31) Представление кодов с помощью матриц. Производящие и проверочные матрицы линейных (n, k)-кодов. Минимальное кодовое расстояние, обнаруживающая и исправляющая способность кода.

1 Любой набор из k линейно независимых векторов линейного n – элементного кода C можно рассматривать как строки матрицы G, называемой производящей или порождающей матрицей (n, k) кода.

Любое кодовое слово V линейного блокового кода (n, k) можно получить умножением вектора U, представляющего информационное слово, на производящие матрицу G размерности k 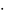n: V =U G.

Принятое слово можно проверить на отсутствие ошибок умножением его на транспонированную проверочную матрицу H^T. Если слово принято без ошибок, результат умножения нулевой: V H^T=0. Проверочная матрица связана с производящие матрицей соотношением G H^T=0.

По матрице G просто определить минимальное кодовое расстояние кода: как наименьшее число единиц в строке или строках матрицы – d_min. Это расстояние показывает обнаруживающую и исправляющую способности кода.

2 Корректирующая способность кода – способность кода обнаруживать и исправлять ошибки. Она определяется только избыточностью кода. От вида кода зависит то, какие вектора ошибок могут быть исправлены или обнаружены. Например, для обнаружения одиночной ошибки комбинация должна из разрешенной при допущении переходить в запрещенную, что возможно когда d_min > 1.

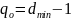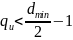Блочный код с кодовым расстоянием d_min может гарантированно обнаружить: ; исправляющая способность кода с заданным d_min, если d_min чётное, то ; если d_min нечётное, то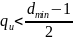

32) Связь между параметрами кода n и k для исправления ошибок различной кратности. Совершенные, плотноупакованные коды. Производящая матрица кода, исправляющего ошибки первой кратности на примере кода (6, 3). Структурная схема кодера на примере кода (6, 3).

1 Связь между n и k для исправления ошибок:

1-й кратности: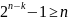

2-й кратности: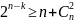

3-й кратности: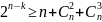

Cовершенный (плотноупакованный) код – код, параметры (n, k) которого переводят неравенство в равенство:

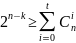
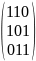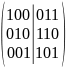2 Исправление ошибок первой кратности для кода (6, 3). Проверочная матрица H , где матрица R – . Производящая матрица G , где 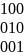– единичная матрица 3 на 3.

Структурная схема кодера для кода (6, 3):

33) Проверочная матрица кода, исправляющего ошибки первой кратности. Структурная схема декодирующего устройства на примере кода (6, 3).

1 Ошибки первой кратности могут быть исправлены, если выполняется условие . Код Хэмминга (7, 4) выполняет это требование. Уравнения формирования:

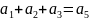
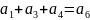
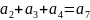
Уравнения проверок:

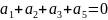
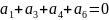
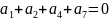
Проверочная матрица:

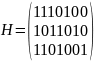
2 Структурная схема декодирующего устройства для кода (6, 3). H

34) Циклические линейные (n, k)-коды. Производящий полином g(x) циклического кода. Его свойства на примере g(x)= x³+ x+1. Признак ошибки в циклических кодах.

Линейный (n, k)-код называется циклическим, если при циклическом сдвиге вправо либо влево на n-1 разрядов кодовой комбинации, принадлежавшей этому коду, образуют комбинации, которые тоже принадлежат этому коду. Для их описания используют полиномы.

При представлении кодовых комбинаций полиномами код задается производящим полиномом g(х) степени (n – к). Свойства производящего полинома на примере g(x)= x³+ x+1. Этот полином соответствует вектору U₀ 1101000. (Код (7, 4))

1 Степень g(x)=n – k. Для примера g(x)=7 - 4 = 3.

2 xⁿ+1 делится на g(x) без остатка: (операции сложения и вычитания по mod2 совпадают)

Частное от деления – проверочный полином h(x)=1+x+x²+x⁴.

3 Производящий полином g(x) – неприводимый, его нельзя разложить на множители.

4 Число d_min для циклического кода можно определить по числу слагаемых в полиноме g(x). Для примера d_min = 3

Признаком ошибки в циклических кодах является синдром ошибки: