28) Гауссовский канал и его пропускная способность, предел пропускной способности.
1 Гауссовский канал – канал связи, для которого выполняются условия: непрерывные сигналы и шумы; канал занимает ограниченную полосу частот F; шум n(t) в канале имеет гауссовское распределение; спектр мощности шума равномерен в полосе частот канала и равен N единиц мощности на единицу полосы частот; средняя мощность полезного сигнала x(t) фиксирована и равна Р; сигнал и шум статистически независимы; шум аддитивен. Пропускная способность:
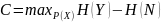
Предельная пропускная способность канала показывает максимальное значение скорости безошибочной передачи информации. Теоретический предел по формуле Шеннона:
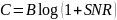
29) Помехоустойчивые коды, классификация. Блочные линейные (n, k)-коды, уравнения формирования контрольных элементов, проверки, синдром ошибки на примере кода (6, 3).
1 Помехоустойчивым кодированием называется кодирование, при котором осуществляется обнаружение либо обнаружение и исправление ошибок в принятых кодовых комбинациях. Классифицируются помехоустойчивых кодов на блочные и непрерывные, блочные подразделяются на: двоичные и не двоичные; имеют векторную алгебру или алгебру полиномов; программный и аппаратный.
2 Линейные блочные коды – это класс кодов с контролем четности, которые можно описать парой чисел (n, k). В процессе кодирования блок из k символов сообщения преобразуется в больший блок из n символов кодового слова, образованного с использованием элементов данного алфавита. 2k – совокупность разрешенных кодовых комбинаций из 2n. Кодовые комбинации удовлетворяют определенным правилам контрольных символов, которые проверяются принимающим аппаратом.
3 Синдром (признаком) ошибки называется совокупностью проверок на ошибки, отличных от нулевой. Синдром ошибки на примере кода (6, 3): допустим ошибка произошла во втором разряде, т.е. правильная комбинация U = 101011, ошибка e = 010000. Вычислим синдром:
,
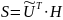так как
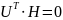вследствие ортогональности, то:
Определим скалярные произведения
вектора
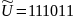с векторами
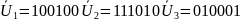
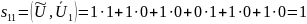
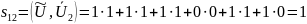
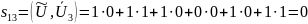
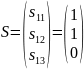– данный вектор – синдром S
и соответствует ошибке во втором разряде
комбинации U.
30) Геометрическое представление линейных (n, k)-кодов. Операции над векторами в пространстве кодовых комбинаций, кодовое расстояние, вес кодовой комбинации, минимальное кодовое расстояние.
Кодовые комбинации линейного (n, k) кода можно представлять в виде векторов n-мерного пространства над полем двоичных чисел {0, 1} – полем Галуа. В поле могут выполняться четыре действия: два прямых – сложение и умножение, и два обратных – вычитание и деление. Пространство векторов – кодовых комбинаций является линейным и замкнутым: сумма (разность) векторов по mod2 дает вектор, принадлежащий этому коду.
Образованное кодовыми комбинациями – векторами линейное пространство означает, что в нем определено правило вычисления расстояния между векторами. Это расстояние называют кодовым расстоянием d. Например, U1=101001 и U2=111010, то d(U1, U2)=3.
Вес – количество ненулевых составляющих в кодовом векторе.
Число кодовых комбинаций – векторов равно 2k из общего числа всех возможных комбинаций – векторов, равного 2n, можно определить (n, k) код как множество векторов, лежащих в k – мерном подпространстве n – мерного пространства кодовых комбинаций. Расстояние между двумя векторами равно весу некоторого третьего вектора и минимальное расстояние для кода равно минимальному весу всех его ненулевых векторов.