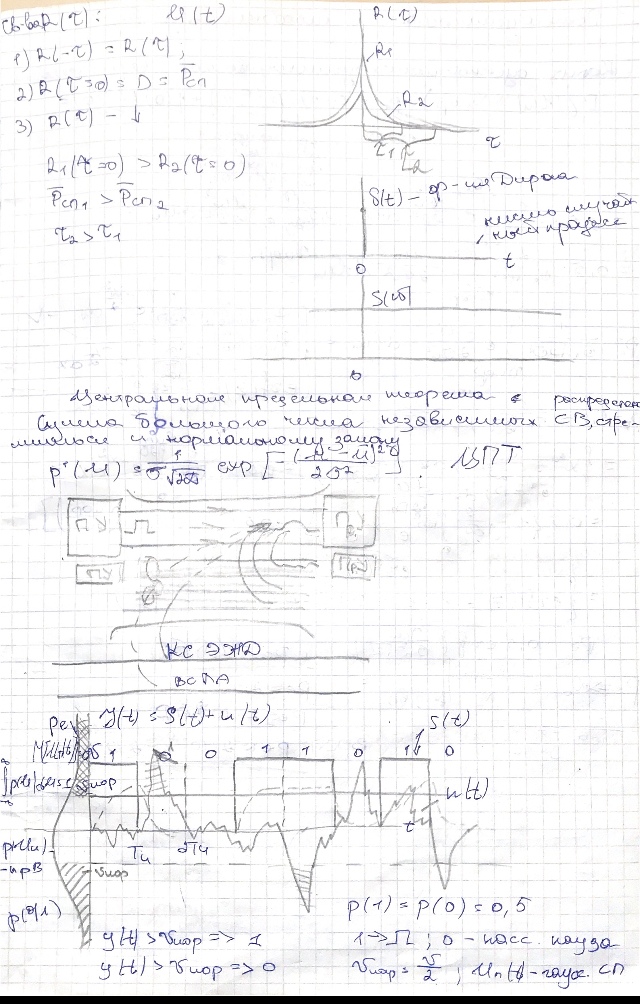
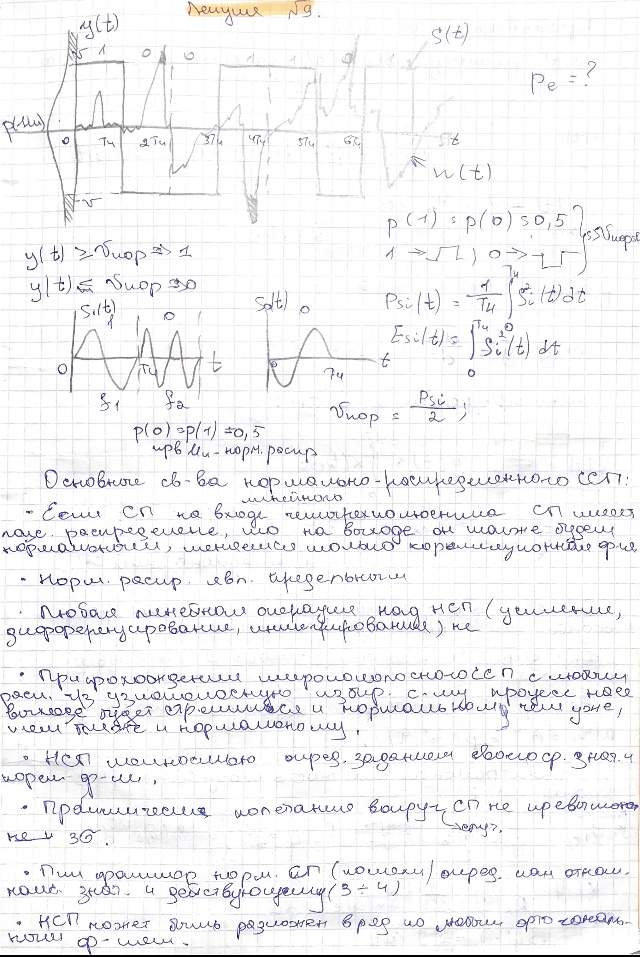
- •1. Информация, сообщение, сигнал, помеха. Классификация сигналов и помех.
- •2. Структурная схема цифровой и аналоговой систем передачи информации. Назначение элементов схемы.
- •3. Энергетические характеристики сигналов. Условие ортогональности сигналов, когерентные сигналы.
- •4. Линейные операторы сигналов. Условия линейности. Линейная зависимость сигналов.
- •5. Линейные пространства сигналов. Сигналы и векторы. Физический смысл нормы и квадрата нормы сигнала.
- •6. Частотное представление сигналов как детерминированных процессов. Системы базисных функций (сигналов). Обобщенный ряд Фурье.
- •11. Условия неискаженной передачи сигналов через линейный четырехполюсник системы передачи информации.
- •12. Дискретизация непрерывных сигналов. Теорема Котельникова. Виды погрешностей. Практическое значение теоремы.
- •13. Дискретное преобразование Фурье. Спектр дискретного сигнала.
- •14. Непрерывные сигналы как случайные стационарные процессы. Вероятностные характеристики случайных сигналов.
- •15. Частотное и временное представление случайных стационарных, эргодических сигналов. Теорема Хинчина – Винера.
- •18. Типы дискретных источников информации, их характеристики. Количество информации в букве сообщения при равновероятности и взаимной независимости букв. Единицы количества информации.
- •25) Теорема Шеннона о пропускной способности дискретного канала с шумами. Способы повышения верности передачи информации.
- •26) Энтропия непрерывного источника информации.
- •27) Объем непрерывного сигнала, объем канала. Способы деления объема канала, системы передачи информации.
- •28) Гауссовский канал и его пропускная способность, предел пропускной способности.
- •29) Помехоустойчивые коды, классификация. Блочные линейные (n, k)-коды, уравнения формирования контрольных элементов, проверки, синдром ошибки на примере кода (6, 3).
- •30) Геометрическое представление линейных (n, k)-кодов. Операции над векторами в пространстве кодовых комбинаций, кодовое расстояние, вес кодовой комбинации, минимальное кодовое расстояние.
- •31) Представление кодов с помощью матриц. Производящие и проверочные матрицы линейных (n, k)-кодов. Минимальное кодовое расстояние, обнаруживающая и исправляющая способность кода.
- •33) Проверочная матрица кода, исправляющего ошибки первой кратности. Структурная схема декодирующего устройства на примере кода (6, 3).
- •20 Количество информации в букве сообщения при неравновероятности и взаимозависимости букв. Энтропия марковского источника.
- •21 Избыточность. Коэффициент сжатия (информативность). Причины избыточности. Методы сжатия сообщений.
- •22 Дискретный канал передачи информации и его характеристики. Количество информации, передаваемое через канал одной буквой. Пропускная способность канала.
- •23 Двоичный симметричный канал и его пропускная способность. Каналы с независимыми ошибками и пакетами ошибок.
14. Непрерывные сигналы как случайные стационарные процессы. Вероятностные характеристики случайных сигналов.
Случайным (стохастическим) процессом X(t), или случайной функцией времени, называется множество W реализаций xr(t) с заданной на нем вероятностной мерой – плотностью распределения вероятностей, где индекс r определяет принадлежность реализации данному множеству.
Чтобы использовать эту возможность необходимо установить вполне определенное соответствие между каждой реализацией сообщения и каждой реализацией сигнала. Поскольку помехи также являются случайными процессами, постольку по реализации принятого сигнала можно лишь с некоторой вероятностью судить о том, какое именно сообщение было передано.
Случайный процесс X(t) считается полностью заданным, если для любого набора моментов времени t1, t2, ..., tn и любых значений сигнала x1, x2, ..., xn можно вычислить вероятность того, что в указанные моменты времени сигнал X(t) принимает значения не превышающие x1, x2,..., xn
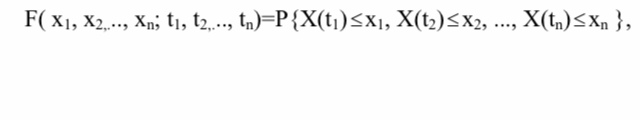
Где
![]() совместная вероятность событий записанных
в скобках.
совместная вероятность событий записанных
в скобках.
X(tk) - случайная величина, так называемое, сечение случайного процесса в момент времени tk.
Функция F(x1, x2, ..., xn; t1, t2, ..., tn)- n-мерная функция распределения вероятностей (ФРВ) процесса. Ее аргументами являются x1, x2, ..., xn, а t1, t2,..., tn- играют роль параметров
Вероятностные характеристики:
математическое ожидание
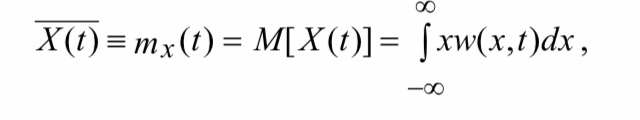
дисперсия- случайного процесса (центральная моментная функция второго порядка) - математическое ожидание квадрата соответствующего центрированного процесса:
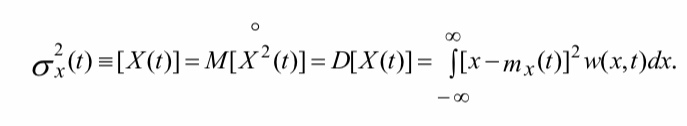
Дисперсия характеризует степень рассеяния возможных реализаций случайного процесса от его среднего значения, физический смысл которой - средняя мощность случайного процесса: сигнала или помехи.
Среднеквадратическое отклонение σХ(t), физический смысл которой – действующее значение напряжения:
![]()
15. Частотное и временное представление случайных стационарных, эргодических сигналов. Теорема Хинчина – Винера.
Сигнал x(t) и его спектр X(f) однозначно выражаются друг через друга. Следовательно, сигнал можно рассматривать в любом из этих эквивалентных представлений — временном или частотном. При этом масштабные параметры этих представлений связаны обратно пропорциональной зависимостью. Допустим, что изменили масштаб по оси времени в k раз (например, воспроизведем запись x(t) с другой скоростью) и найдем спектр функции x(k⋅t):
Xk(f) = ∫x(k⋅t)⋅exp[j2πft]dt = (1/k)⋅X(F/k)
Как видим, масштаб по частотной оси изменился в 1/k раз. Более того, из свойств преобразования Фурье следует, что сигналы с ограниченной длительностью имеют спектры неограниченной ширины, а сигналы с ограниченной полосой частот длятся бесконечно долго. Этот математический результат находится в противоречии с практикой: в реальности все сигналы конечны по длительности и ограничены по спектру. Тот факт, что аналитическая функция времени не может быть одновременно ограниченной и по длительности и по ширине спектра является, как видим, не свойством реальных сигналов, а свойством данной модели сигналов.
Говорить об одновременной ограниченности сигналов по времени и по спектру оказывается возможным при использовании энергетического критерия точности: сигнал считается имеющим конечную длительность Т, если в этом интервале времени сосредоточена основная часть всей энергии функции x(t). В то же время и ширина спектра F сигнала определяется как область частот, содержащая эту же часть всей энергии спектра X(f):
∫x2(t)dt = ∫|X(f)|df = μ∫x2(t)dt = μ∫|X(f)|df
Здесь величина M меньше единицы, хотя достаточно близка к ней, а величина 1-M характеризует косвенным образом точность, о которой шла речь.
Теперь можно говорить о том, какую «площадь» на плоскости «частота-время» занимает тот или иной сигнал. Если строго следовать теории Фурье-преобразований, то получим, что эта площадь для всех сигналов бесконечна. Но для большинства из них энергетический критерий позволит ограничить ее естественным образом.
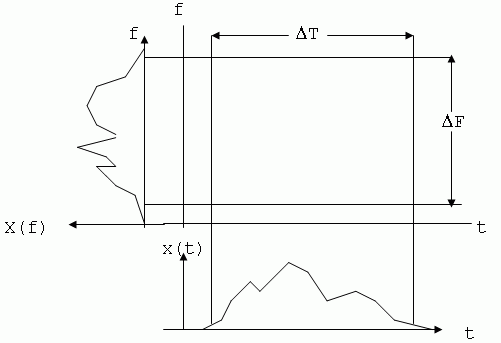
Рис.9.1 — Иллюстрация частотно-временной неопределенности сигнала
Меняя форму сигнала, можно изменить и площадь на плоскости «время-частота», которую он занимает. Оказывается, что уменьшать эту площадь можно лишь до некоторого предела. Этот предел достигается на кривой, являющейся гармоническим колебанием, которое модулировано по амплитуде гауссовым импульсом. Существование предела, ниже которого нельзя сжать площадь сигнала, занимаемую им на плоскости «частота-время», и называется (по аналогии с принципом неопределенности в квантовой механике) принципом частотно-временной неопределенности сигналов:
ΔF ⋅ ΔT = const ≥ 0
Теорема Хинчина-Винера
Энергетический
спектр и автокорреляционная функция
случайного процесса являются неслучайными
функциями, связанными между собой.
Установим эту связь. Рассмотрим
реализацию ![]() случайного
процесса длительностью
случайного
процесса длительностью ![]() и
ее копию
и
ее копию ![]() ,
сдвинутую на интервал времени
,
сдвинутую на интервал времени ![]() .
Известно, что энергетический спектр и
автокорреляционная
функция детерминированного сигнала
связаны между собой парой преобразований
Фурье. Тогда с учетом выше приведенного
предположения о том, что реализация
и
ее копия
нам
известны, можно записать
.
Известно, что энергетический спектр и
автокорреляционная
функция детерминированного сигнала
связаны между собой парой преобразований
Фурье. Тогда с учетом выше приведенного
предположения о том, что реализация
и
ее копия
нам
известны, можно записать
![]() .
.
Разделим обе части этого равенства на
![]() ,
(5.62)
,
(5.62)
и
устремим ![]() .
.
Тогда
в соответствии с (5.51) левая часть равенства
(5.62) представляет собой автокорреляционную
функцию ![]() .
Учитывая (5.59) равенство (5.62) можно
представить следующим образом
.
Учитывая (5.59) равенство (5.62) можно
представить следующим образом
![]() .
(5.63)
.
(5.63)
Но это есть обратное преобразование Фурье, связывающее АКФ случайного процесса с его энергетическим спектром. Очевидно, если существует обратное преобразование, значит, существует и прямое преобразование Фурье
![]() ,
(5.64)
,
(5.64)
связывающее энергетический спектр с АКФ.
Таким образом, АКФ случайного процесса и его энергетический спектр связаны между собой парой преобразований Фурье. Впервые эта связь была установлена советским математиком А. Хинчиным и независимо от него американским ученым Н. Винером. Поэтому соотношения (5.63) и (5.64) носят название теоремы Винера–Хинчина.
Так
как автокорреляционная функция
и
энергетический спектр ![]() являются
вещественными четными функциями, можно
отказаться от комплексной формы записи
преобразования Фурье и перейти к другой
форме
являются
вещественными четными функциями, можно
отказаться от комплексной формы записи
преобразования Фурье и перейти к другой
форме
![]() ,
(5.65)
,
(5.65)
![]() .
(5.66)
.
(5.66)
Из этих выражений следует
![]() ,
(5.67)
,
(5.67)
![]() .
(5.68)
.
(5.68)
Но ![]() ,
откуда
,
откуда
![]() ,
,
что совпадает с (5.60).
В случае, когда энергетический спектр описывается функцией циклической частоты (5.61), выражения (5.65) – (5.68) приобретают вид
![]() ,
(5.69)
,
(5.69)
![]() .
(5.70)
.
(5.70)
![]() ,
(5.71)
,
(5.71)
![]() .
(5.72)
.
(5.72)
16-17.