12. Дискретизация непрерывных сигналов. Теорема Котельникова. Виды погрешностей. Практическое значение теоремы.

Реальные сигналы имеют ограниченную полосу частот. Такие сигналы обладают замечательным свойством, впервые уставленным В. А. Котельниковым и выраженным в его теореме, играющей фундаментальную роль в теории и технике передачи сигналов.

Если в общем случае непрерывная функция времени определяется на конечном интервале бесчисленным множеством своих мгновенных значений, то функции времени с ограниченным спектром согласно теореме Котельникова на конечном интервале определяются конечным множеством своих значений.

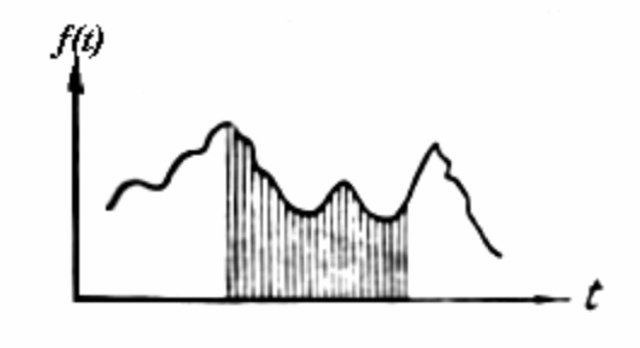
Отсутствие в функции частот выше некоторой граничной накладывает определенные ограничения на ее изменение в достаточно малом интервале времени t . Поэтому через точки, изображающие мгновенные значения функции и взятые через определенный интервал времени друг от друга, можно провести кривую одним единственным способом.

Теорему В. А. Котельникова можно сформулировать в следующем виде:

Любой сигнал f(t), спектральная плотность которого отлична от нуля в полосе частот в 0  f , можно точно восстановить (интерполировать) по ее отсчетам f (kt), взятым через интервалы Δt  1/2F, где F— высшая частота в спектре сигнала, с помощью ряда Котельникова

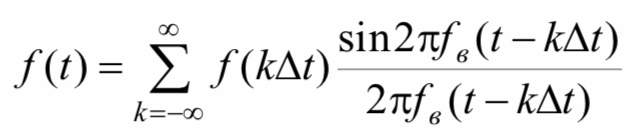
где f (kt) - значения непрерывного сигнала в точке отсчета сигнала t  kt.

Функциями разложения в ряде Котельникова являются так называемые функции отсчетов

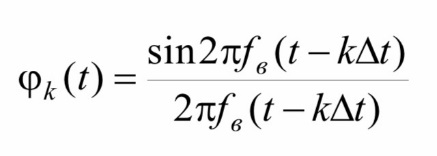
Эти функции обладают свойством

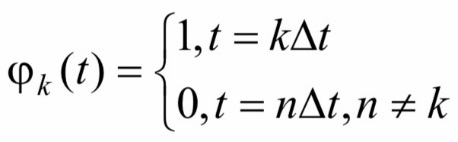
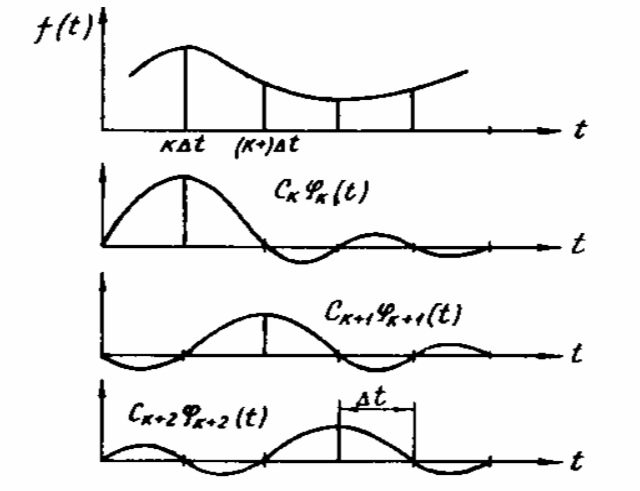
Таким образом, в момент времени t  kt сумма ряда (7.1) определяется лишь k-ым слагаемым, все остальные члены ряда в этот момент времени обращаются в нуль. Разложение функции в ряд Котельникова иллюстрируется на рис.

Виды погрешностей:

• Погрешность, вызванная ограничением длительности сигнала

• Погрешность, вызванная ограничением ширины спектра сигнала

Применение на практике:

На практике для восстановления сигнала (АИМ) используются реальные фильтры нижних частот с граничной частотой в 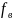. В этом случае для выделения модулирующего сигнала необходимо частоту следования импульсов 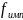выбирать из условия в .

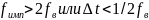Теорема Котельникова лежит в основе всех видов импульсной модуляции и методов временного уплотнения каналов.

Теорема Котельникова позволяет также количественно подойти к оценке пропускной способности систем ЖАТС при заданных сигналах. Пусть, например, сообщение передается с помощью набора элементарных сигналов вида 'да' и 'нет'. Принимая за единицу пропускной способности канала число элементарных посылок за 1сек (эта единица называется ''бодом''), получим, что по каналу с полосой частот можно передавать не более 2 бод. Следовательно, в этом случае пропускная способность или, точнее, скорость передачи не может быть больше 2 бод на 1 Гц полосы частот.

13. Дискретное преобразование Фурье. Спектр дискретного сигнала.

Дискретных преобразований достаточно много (преобразования Фурье, Хаара, Уолша, Гильберта и др.), однако самым распространенным является дискретное преобразование Фурье (ДПФ), с помощью которого осуществляют спектральный анализ сигналов:

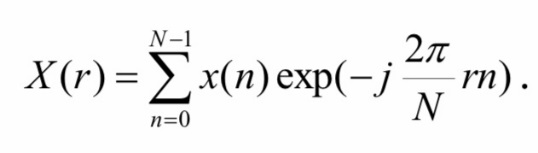
Если соотношение переписать в виде:

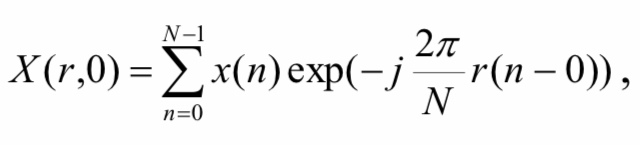
тогда становится очевидным, что ДПФ можно трактовать как результат цифровой фильтрации сигнала x(n) гребенкой узкополосных цифровых фильтров – с той лишь особенностью, что из результата фильтрации оставляется только один отсчет.

При достаточно большом значении параметра N вычисление ДПФ весьма трудоемко. Благодаря изобретению алгоритма быстрого преобразования Фурье (БПФ) (1965 год – Кули, Тьюки) стало возможным весьма эффективное вычисление ДПФ ( N log N арифметических операций вместо операций).

Определим связь между спектром X(jw) аналогового сигнала x(t) и спектром X_Т(jw) дискретного сигнала x_Т(t), определенного моделью (19.2). Учитывая, что x_Т(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала

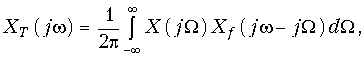 (19.4)

где X_f(jw) – спектральная плотность дискретизирующей последовательности (19.1).

Для нахождения X_f(jw) разложим f(t) в комплексный ряд Фурье (5.6):

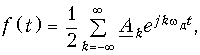 (19.5)

где w_д = 2p/Т – частота дискретизации,

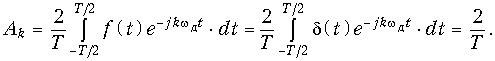
Отсюда согласно (9.42) получаем

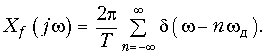(19.6)

Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства d-функции окончательно получим

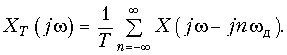 (19.7)

Из (19.7) следует важный вывод: спектр дискретного сигнала x_T(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных на оси частот через одинаковые интервалы.

Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2). Если же использовать вместо дискретизирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр X_Т(jw), энергия которого убывает с ростом w («копии» X(jw) с ростом w уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.

Спектр дискретного сигнала X_Т(jw) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t Õ 0).

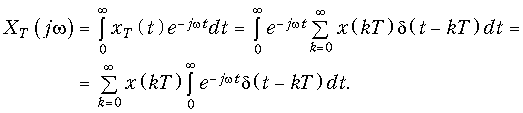
Отсюда с учетом фильтрующего свойства d-функции получим прямое преобразование Фурье для дискретных сигналов.

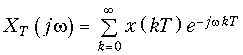 (19.8)

и обратное преобразование Фурье:

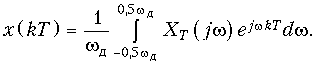 (19.8)

На практике в формулах (19.8), (19.9) часто вместо зависимости X_Т(jw) рассматривают зависимости X_Т(jf), которые легко можно получить путем замены w = 2pf.

Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом f_д = 1/Т.