6. Частотное представление сигналов как детерминированных процессов. Системы базисных функций (сигналов). Обобщенный ряд Фурье.
Спектральным представлением детерминированного сигнала s(t) называется его представление в виде суммы конечного или бесконечного числа гармонических составляющих. Основой спектрального представления сигналов является преобразование Фурье.
Сигнал
на
интервале
может
быть записан в форме обобщенного ряда
Фурье:
.
Если
– вектор, то последнее выражение можно
интерпретировать как разложение по
некоторому базису, а коэффициенты
могут
рассматриваться как проекции вектора
на координатные оси, заданные системой
функций
,
образующих базис.
Базисные
функции
должны
быть попарно ортогональнымы, т.е.
.
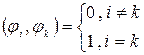Если базисные функции системы имеет единичную норму, то они образует ортонормированный базис.
При выполнении указанных условий коэффициенты обобщенного ряда Фурье находятся следующим образом:
.
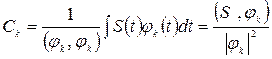Обобщенный
ряд Фурье содержит бесконечное число
членов. На практике приходится ограничивать
ряд конечным числом членов
.
Это
приводит к появлению ошибки
аппроксимации:
.
Обычно
рассматривают норму ошибки
.
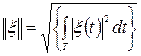(8)
Одним
из важных свойств базисных функций
является полнота. Базисные функции
образуют полную систему, если норма
ошибки с ростом
уменьшается.
Наиболее известной является
тригонометрическая система базисных
функций.
7. Спектр напряжения периодического сигнала, спектр амплитуд, спектр фаз.
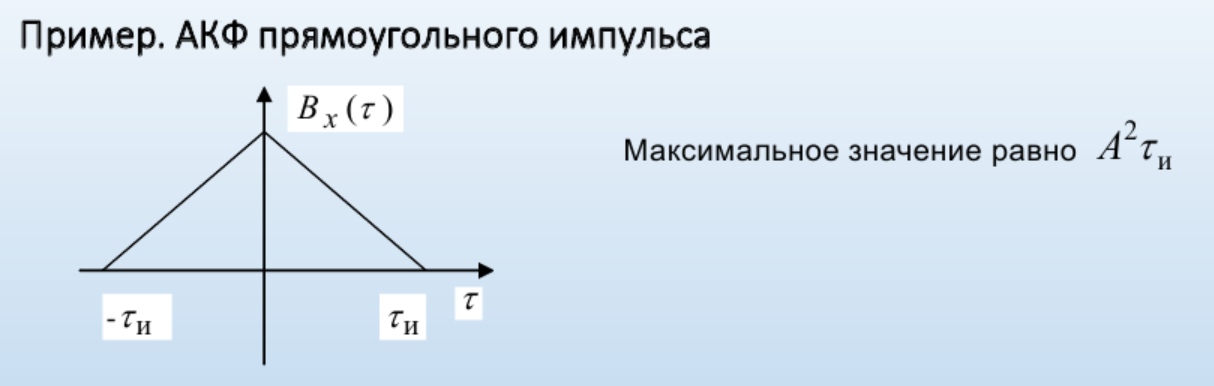
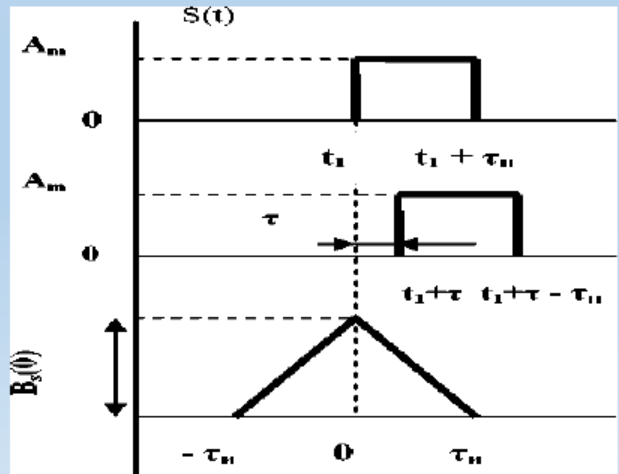
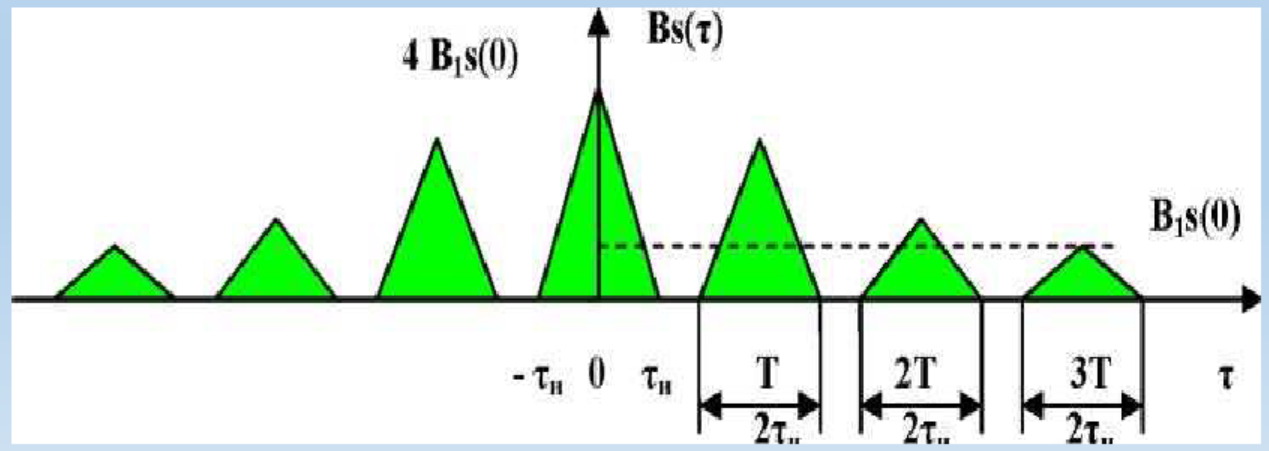
8. Спектр мощности и функция автокорреляции детерминированных сигналов. Связь параметров сигнала с значениями функции автокорреляции на примере прямоугольного импульса.
9. Свойства преобразования Фурье. Равенство Парсеваля. Теорема Релея.
Для периодического сигнала:
Для непериодического сигнала:
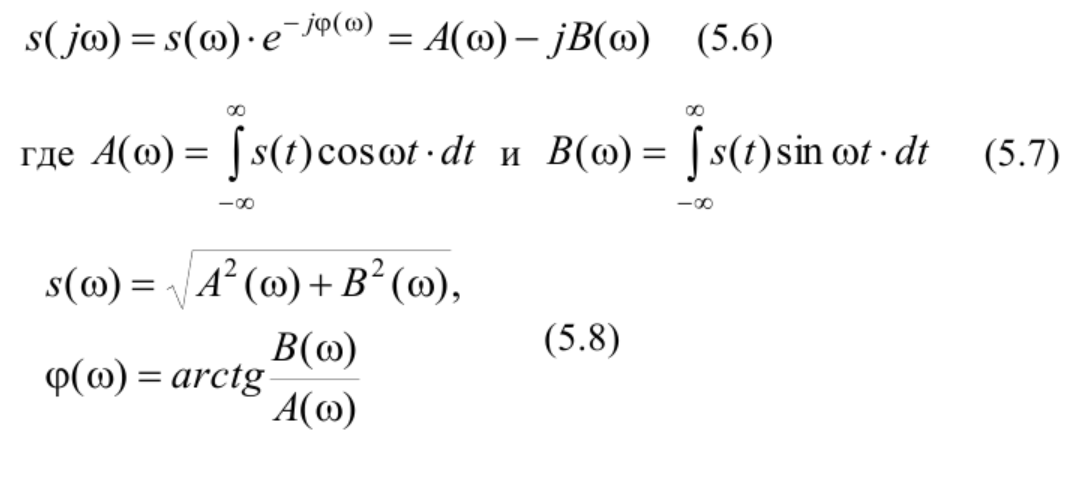
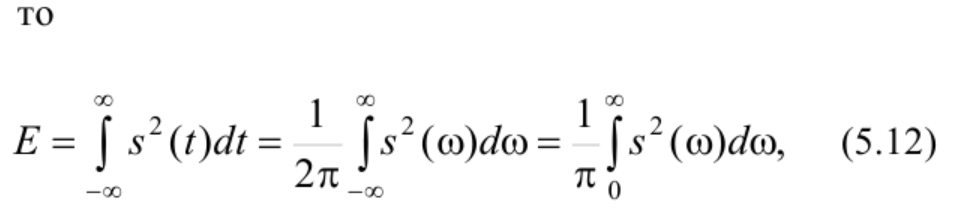
10.
Реакция линейного элемента системы
передачи на
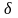–импульс.
Прохождение детерминированного сигнала
через линейный элемент системы передачи.
11. Условия неискаженной передачи сигналов через линейный четырехполюсник системы передачи информации.
Определим сначала условия неискаженной передачи сигналов. Будем считать сигнал на выходе системы неискаженным, если он отличается от входного только масштабом и сдвигом во времени на величину t0 , т.е. y(t)=ax(t-t0)
Из этого условия видно, что система, не искажающая сигнал, должна быть линейной
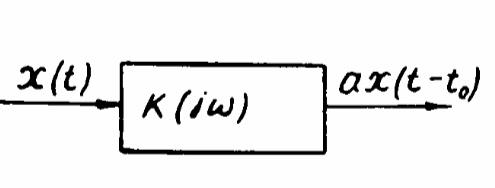
Определим ее передаточную функцию k( j).
Спектр сигнала y(t) определяется выражением s ( j) s ( j)k( j)
С другой стороны, этот же спектр можно определять обратным преобразованием Фурье от y(t) :
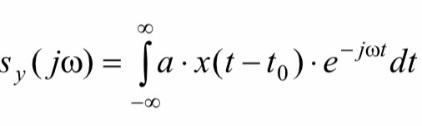откуда
после замены переменных
t
t0 находим
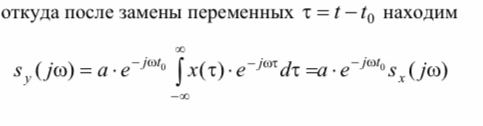
Сравнивая эти выражения, для передаточной функции неискажающей линейной системы получим
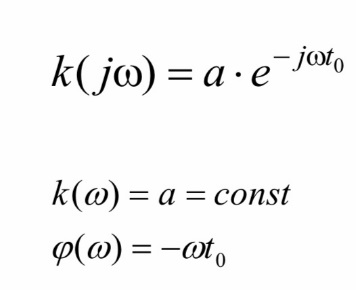
Таким образом, передаточная функция хотя бы в полосе частот входного сигнала должна быть идеальной: амплитудно-частотная характеристика должна быть постоянной, а фазо-частотная – линейной. Отсутствие искажений в этом случае иллюстрируется на рис. для сигнала, состоящего из двух гармонических колебаний кратных частот при 1 t0 и 2 t0 2.
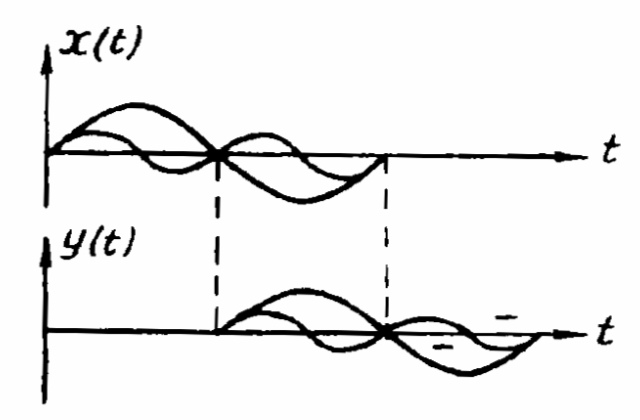
В том случае, если характеристики системы не будут удовлетворять приведенным условиям, сигнал при прохождении через нее будет искажаться.