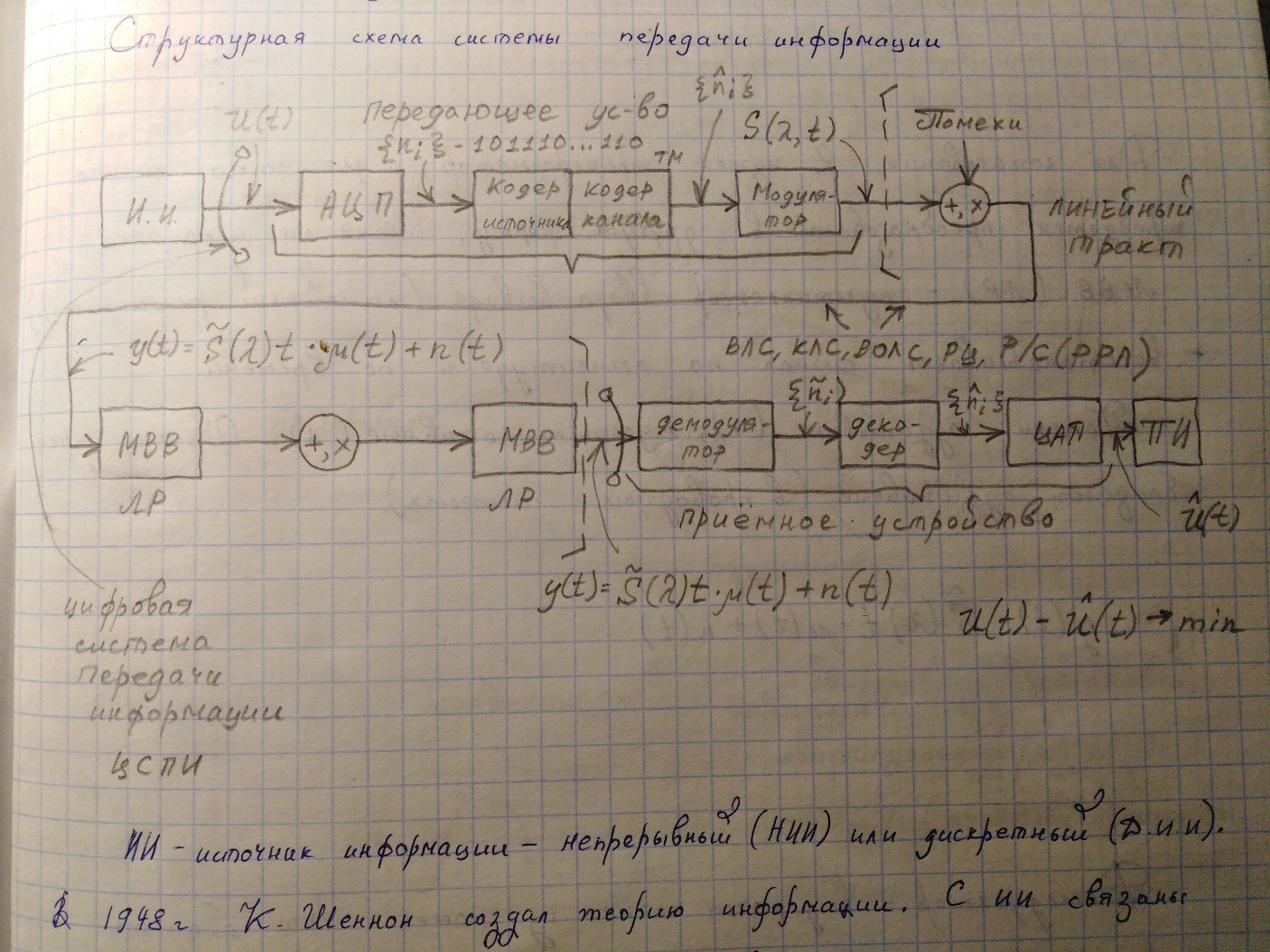
2. Структурная схема цифровой и аналоговой систем передачи информации. Назначение элементов схемы.

3. Энергетические характеристики сигналов. Условие ортогональности сигналов, когерентные сигналы.

Энергия и мощность детерминированного сигнала – это важные параметры сигнала, поскольку, как правило, требуется, чтобы информация передавалась с заданным качеством при минимальных затратах и энергии.

Если детерминированный сигнал S(t) представляет собой изменение напряжения или тока, то его мгновенная мощность, выделяемая на сопротивление в 1 Ом равна:

P(t)=S²(t).

Энергия сигнала в интервале времени (t_а, t_в):

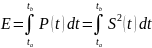
Средняя мощность сигнала в этом же интервале Р_ср = Р:

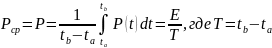
Например, в одном периоде

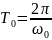
гармонического сигнала S(t)=cos(₀T)

содержится энергия:

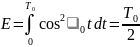
а средняя мощность составляет:

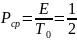
Если на интервале T = t_b-t_a заданы два детерминированных сигнала S₁(t) и S₂(t), то энергия их суммы определяется следующим образом:

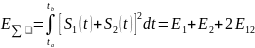
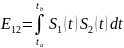
где Е₁₂ – взаимная энергия сигналов (энергия их взаимодействия).

Сигналы S₁(t) и S₂(t) – называют ортогональными если: Е₁₂ = 0, в этом случае

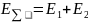
Когерентность (от лат. cohaerens – «находящийся в связи») – в физике скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.

4. Линейные операторы сигналов. Условия линейности. Линейная зависимость сигналов.

5. Линейные пространства сигналов. Сигналы и векторы. Физический смысл нормы и квадрата нормы сигнала.

Для теоретического исследования сигналов необходимо построить их математические модели.

- Классификация сигналов осуществляется на основании существенных признаков соответствующих математических моделей. Принято различать одномерные и многомерные, детерминированные и случайные, аналоговые и дискретные сигналы. Разновидностью последних являются цифровые сигналы.

- Принцип динамического представления позволяет описывать сигналы, учитывая их поведение как «в прошлом», так и «в будущем».

- Для динамического представления используются два элементарных сигнала – функция включения и дельта-функция (функция Дирака).

- Путем введения структуры некоторые множества сигналов могут быть превращены в линейные функциональные пространства.

- Система линейно независимых векторов образует координатный базис, по которому можно разложить произвольный вектор, принадлежащий линейному пространству.

- Аналогом длины вектора в линейном пространстве сигналов служит его норма. Квадрат нормы называется энергией сигнала.

- Линейное пространство сигналов становится метрическим пространством, если определить метрику – расстояние между двумя векторами.

- Чтобы найти угол между двумя элементами линейного пространства, вводят понятие скалярного произведения, пропорционального взаимной энергии сигналов. Если скалярное произведение равно нулю, то сигналы ортогональны.

- Представление сигнала в виде разложения по ортонормированному базису называют обобщенным рядом Фурье. Коэффициентами такого ряда служат скалярные произведения разлагаемого сигнала и соответствующих базисных векторов.

- Энергия сигнала равна сумме энергий всех членов обобщенного ряда Фурье.

- Разложение сигнала по ортонормированному базису обеспечивает минимум энергш ошибки аппроксимации.

- Процесс извлечения полезной информации, содержащейся в сигнале, можно представить себе как аппаратурное определение числовых значений коэффициентов обобщенного ряда Фурье этого сигнала.

Сигнал должен принадлежать множеству квадратично-интегрируемых на отрезке сигналов:

.

Такое множество сигналов образует пространство сигналов . Отрезок интегрируемости может быть как конечным, так и бесконечным интервалом.

Пространство замкнуто относительно линейных операций, т.е. если и , то и . Поэтому его называют линейным векторным пространством.

Сигналы и рассматриваются как векторы в линейном пространстве, для которых определено скалярное произведение:

И норма вектора (длина вектора): .